【机器学习300问】59、计算图是如何帮助人们理解反向传播的？

在学习神经网络的时候，势必会学到误差反向传播，它对于神经网络的意义极其重大，它是训练多层前馈神经网络的核心算法，也是机器学习和深度学习领域中最为重要的算法之一。要正确理解误差反向传播，不妨借助一个工具——计算图。

一、计算图是什么？

（1）计算图的定义

计算图是一种用来表示数学表达式和计算流程的数据结构（有向图），是一个将复杂计算过程可视化的图形模型。计算图中有节点（vertices）和边（edges）的概念，节点通常表示计算操作或者函数，而边表示数据或参数的流动，一个节点的输出可以成为另一个节点的输入。

（2）举例说明

举例说明一下，假设有这样一个数据表达式 $v=a+u$ 它的计算图可以画成这样：

现在，在这个操作的前后分别再加上个操作 $u=bc$ 和 $J=3v$ ，那么这个新的复杂一点的计算图可以画成这样：

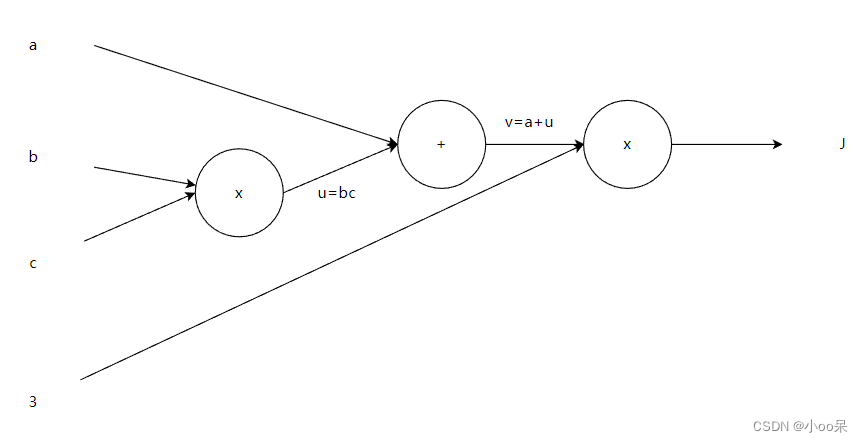
（3）计算图的主要用途和优点

① 直观的表现计算关系

计算图中的节点代表数值或者变量，而边则表示节点之间的依赖关系，例如加法、乘法或其他复杂操作。这种图形化的表示方式直观展示了计算步骤及其顺序。

② 进行局部计算

无论全局计算是多么的复杂，都可以通过局部计算使各个节点致力于简单的计算，从而简化问题。

③ 内存优化和提升计算效率

计算图可以缓存中间计算结果，避免重复计算，提高内存使用效率和减少运行时间。

④ 自动微分和计算梯度

在训练神经网络时，需要计算损失函数相对于所有权重的梯度来进行优化。计算图能够轻松实现自动微分，因为每一步计算的梯度可以通过链式法则从输出反向传播至输入，这一过程被称为反向传播。

二、计算图怎么实现正向传播？

（1）正向传播的过程

初始化节点值：在计算图中，输入层的每一个节点都会被赋予一个初始值，这通常是实际输入数据，比如一组特征向量。
应用权重和偏置：在计算到达隐藏层之前，输入层的节点值与对应的权重（weights）相乘。此外，每个隐藏层节点都会加上一个偏置值（bias）。这个操作对应计算图中的一个节点，其上一层的所有输出都会汇聚到这个点。
激活函数：在隐藏层节点加上权重和偏置之后，通过一个激活函数（如ReLU或Sigmoid）来引入非线性。激活函数的选择对网络的性能有着直接影响。此操作通常在计算图中表示为另外一个节点。
传递到下一层：经过激活函数处理后的值被传递到下一层，如果有多个隐藏层，则这一过程会重复进行，直到达到输出层。
输出层的计算：最后，当信息流到达输出层，相同的过程（加权、求和、添加偏置以及激活）会得到一个输出值。在分类任务中，这个值通常会通过softmax函数被转换成概率分布。
得出预测结果：这个最终经过激活处理的输出层的值就是网络的预测结果。对于不同的任务，比如分类、回归或其他，输出层会以不同的方式处理这些值来适应特定任务的需求。

（2）正向传播举例

以逻辑回归任务为例，来介绍一下上述过程的具体实现。先把逻辑回归所用到的公式说明一下：

$z=w^Tx+b=w_1x_1+w_2x_2+b$

假设数据样本只有两个特征 $x_1$ 和 $x_2$ ，为了计算 $z$ ，我们需要输入参数 $w_1,w_2,b$ ，因此 $z$ 的公式如上所示。逻辑回归模型的公式定义如下，其中 $\hat y$ 是预测值， $\sigma(z)$ 是sigmoid函数：

$\hat y = a = \sigma (z)$

$\sigma(z)=\frac{1}{1+e^{-z}}$

逻辑回归的损失函数定义如下，为了简单理解我给出的是单个样本的代价函数：

$L(a,y)=-[ylog(a)+(1-y)log(1-a)]$

其中，a是逻辑回归的输出，y是样本的标签值（真实值）。现在我们画出这个计算图。

（3）人话理解正向传播

正向传播很好理解，就是你把数值带入上面这个图，从左向右正向一次计算每一个节点中的数学表达式，就得到了最终的输出。虽然很好理解，但我在这里特意说明一下，在正向传播过程中，“传播”的实际上是信号数据（就是你通过节点式子算出来的值）。

中间怎么算的你可以忽略，正向传播就是在干这样一件事情，输入一组样本加上对应权重和偏置，得到一个最终的损失函数值。进一步理解就是说，不同的一组样本+权重+偏置会得到不同的损失函数值。因为神经网络学习的目的就是得到最优的权重和偏置（w,b合称参数），所以我把每次输入的训练样本都设成一样，但是允许更换许多许多组不同的权重+偏置的组合，就会得到许多许多不同的损失函数值。

我想要做的事情就是想得知：当损失函数值最小的时候，对应的权重+偏置是多少，此时的参数就是最优参数。要想达成这个目的就需要误差反向传播。

三、计算图怎么实现反向传播？

（1）反向传播的过程

计算图在实现反向传播的过程中扮演了关键角色，它提供了一种结构化的表示，使得能够高效且准确地计算神经网络中所有参数相对于损失函数的梯度。下面是利用计算图进行反向传播的基本步骤：

计算损失函数值：反向传播的起点是损失函数，使用预测结果和实际标签计算损失函数的值。损失函数衡量模型预测结果与真实值之间的差距。
初始化梯度：在损失节点处，对自身的梯度进行初始化，通常这个梯度是1，因为损失函数关于自身的导数是1。初始化所有参数（权重和偏置）的梯度为零。
利用链式法则计算每个节点梯度：从输出层开始，根据损失函数的梯度（即损失函数对输出层节点的导数），利用链式法则，将计算得到的梯度沿着计算图反向传播到每个权重和偏置。每个节点的梯度是其下游节点梯度与其本地导数的乘积累积而成。
梯度聚合：在计算图中，一个节点可能有多个输入，每个权重可能会受到多条路径上的梯度影响，需要将所有这些影响累积起来，得到最终的梯度值。
参数更新：当所有参数的梯度都通过反向传播计算出来后，根据优化算法（如梯度下降法或其变种）使用这些梯度来更新相应的权重和偏置。

（2）反向传播举例

以一个输入节点的输入层、一个sigmoid作为激活函数的隐藏层，一个输出节点的输出层为例。先给出他的正向传播计算图：

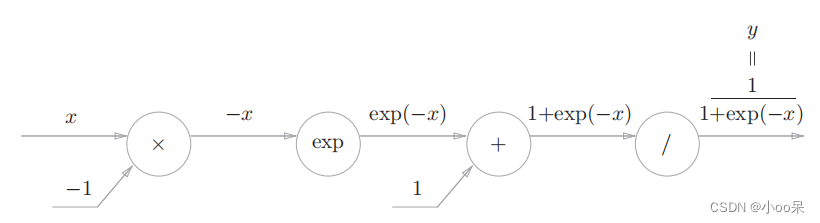
除了乘法和加法节点之外，还出现了自然数e为底的幂运算和除法节点。除法节点处的导数公式是：

$y=\frac{1}{x}$

$\frac{\partial y}{\partial x}=-\frac{1}{x^2}=-y^2$

反向传播时，会将上游的值乘上 $-y^2$ 后再传给下游。计算图如下：

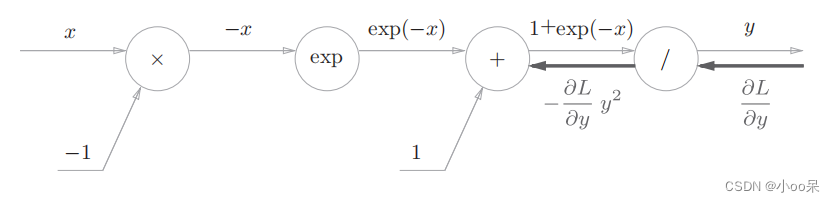
加法节点会原封不动的传给下游，计算图如下图所示：

exp节点的 $y=e^x$ 它的导数就是它自己，所以上游的值要乘上这个exp(-x)后再传给下游，计算图如下所示：

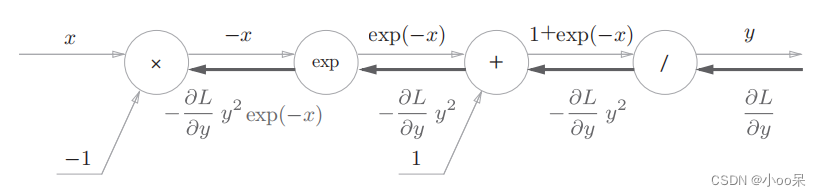
乘法节点将正向传播时的值翻转后做乘法，因此这里需要乘以-1，计算图如下所示：

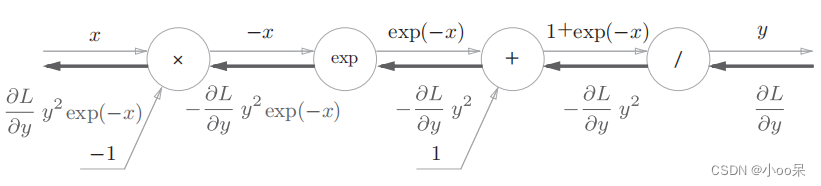
（3）人话理解反向传播

既然神经网络学习的目的是学到最优权重w和偏置b(合称参数），这个“最优”怎么定义？就是指能让损失函数值最小的参数，就是最优参数。要想得到最优参数，那么我就得回答这样一个问题，即怎么根据现在误差值来调整w和b才能让误差值变小呢？这个问题可以拆解成另外两个小问题：

① 误差和参数之间它们是怎么互相影响对方的？

建立参数与误差值之间的公式，也就是损失函数。通过损失函数就找到了他们之间的桥梁，就能知道误差想要表小，参数该如何变化。

② 如果误差变化了参数该如何变化？

为了使误差减小，我们需要根据损失函数关于参数的梯度来调整参数。梯度给出了损失函数在当前参数值处的斜率，指向损失函数值下降最快的方向。这里有必要重提一下导数的定义：“一函数在某一点的导数描述了这个函数在这一点附近的变化率”，也就是自变量变，函数值跟着变，还不是简单的跟着变多少，还知道变的快慢。假设我有 $w_1,w_2,b$ 三个参数，对损失函数求偏导就能知道每一个参数，它对应要变化多快或多慢，将这种变化率 $\partial w_1,\partial w_2,\partial d$ 反向传给原来的 $w_1,w_2,b$ ，就能指导参数变化的具体值：

$w_{new}=w_{old}-a\partial w$

$b_{new}=b_{old}-a\partial b$

所以反向传播，“传播”的是误差信号在神经网络中的梯度（就是指导参数该怎么变的变化率）。具体来说，它并不是传播实际的输入数值或预测结果，而是传播从输出层到输入层的损失函数相对于网络中每个参数的梯度（梯度就是偏导数的向量表示）。这些梯度信息表明了在当前参数设置下，损失函数增大或减小的趋势。也就是说，告诉我们应当如何调整权重和偏置才能降低损失函数的值。

③ 举个小孩儿做题的例子

反向传播就好比你正在教一个小孩做一道复杂的数学题。小孩做完题后，你会检查答案是否正确，如果不对，你会告诉他哪里错了，让他改正。在这个过程中：

正向传播：就像是小孩按照步骤一步步计算题目。比如说他要计算 (a+b) × c，他先算出 a+b 的结果，然后再把这个结果乘以 c 得到最后的答案。

损失函数：相当于你用来判断小孩答案对错的标准。如果他的答案离正确答案差很多，你就有一个衡量错误程度的“分数”。

反向传播：是你指导小孩如何改正错误的过程。假设他最后的答案错了，你会告诉他：“你计算的最后一步有问题，你需要知道是因为 c 值没乘对还是前面 a+b 的结果就不对。”于是你从最后一个步骤开始，告诉小孩每一步对他最后答案的影响有多大（也就是计算梯度），这样他才能有针对性地调整自己的计算步骤，以便下次做得更好。

这里的关键就在于，你没有告诉他正确答案（也就是损失函数最小的时候对应的参数，有时候正确答案你自己都不知道），而是通过提示让他自己一步步去找到正确答案。