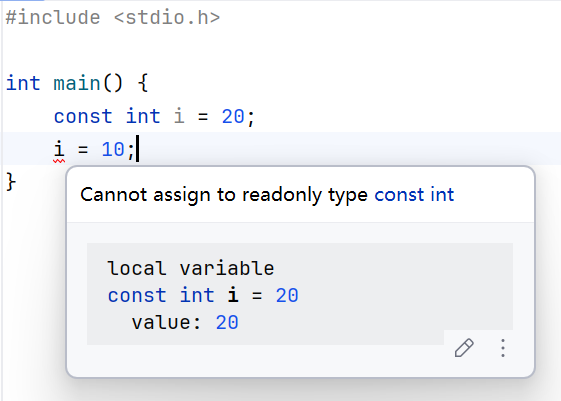
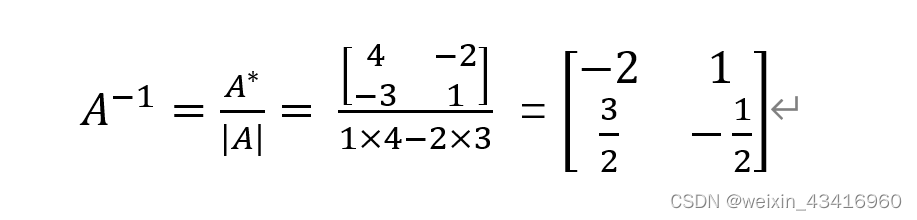bug描述
初始化页面,文件上传框无法出现:

但点击一次选择框以后,就会出现:

真的很神奇。。。
下面逐步排查看看是什么原因。
设想一:
选择框与文件框不可同时存在,删掉选择框看看:

还是不行。不是选择框问题。但是有发现,点击原本选择框位置,文本框会出现。
好了,看看文件框的范围:
排查,文件框的范围:
检查元素,得到:

那么可以得知:
点击了选择框才出现有可能是因为,刚好触发了文件框的范围。
排查 文件框样式
文件框的美化原理是设置文件框足够大,并且透明,底下用其他图片做美化,然后用户点击了图片其实是点击上层的文件框的,样式如下:

改一下,只保留大小,试试:

然后结果为:


还是一样,不过样式已经出来了。
也就是说,这bug与样式关系不大。
结论
嗯。。。最后发现是 逻辑中包含了 隐藏input的开关,因为某些原因,即使修改了开关=显示,但是实际界面没有重新渲染,点击了select以后界面才渲染,这时候连同文件框也正常渲染,所以,解决方案是:

修改开关以后强制刷新下界面。