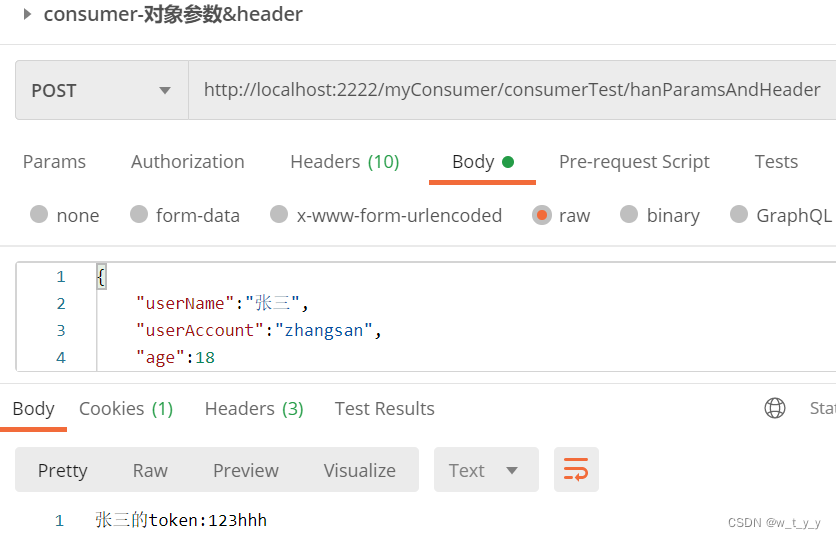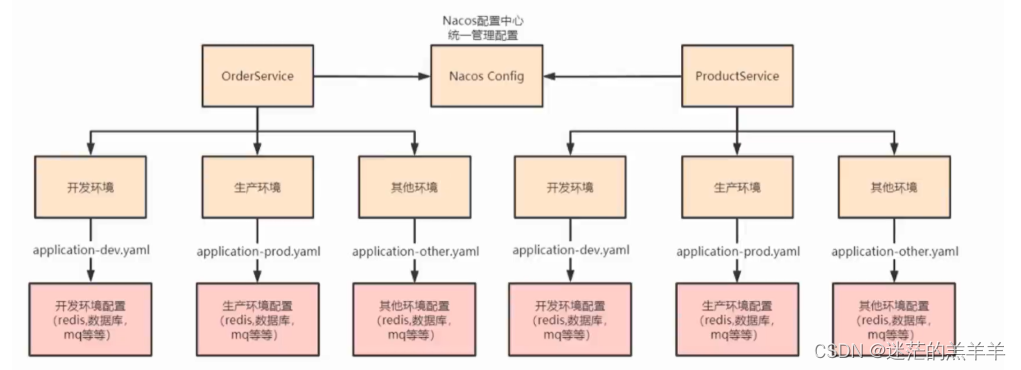
配置中心可以做集中式的服务配置管理，比如配置一些数据库连接的URL，一些共用的配置且可动态调整的参数。如果不采用集中式的管理，会导致修改起来特别麻烦，一个个的修改特别繁琐。

        Nacos Config配置中心中采用的是客户端拉取数据，即客户端从服务端上拉取最新的数据，服务端配置了客户端所需的数据项时，客户端会设置一个定时任务来检查自己监听的配置项的数据，发送一个http请求，根据本地缓存Cache Data中CheckMD5值与服务端的MD5进行比较，如果不一致，则说明配置项发生了改变，就要重新的拉取新的数据，新的配置拉取到本地的CacheData后，还会重新计算本地MD5的值。

        拉取的优势在于减轻了Nacos服务的压力。