LeetCode题练习与总结：N皇后

news2024/11/26 23:25:57

一、题目描述

按照国际象棋的规则，皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。

n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题 的解决方案。

每一种解法包含一个不同的 n 皇后问题 的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

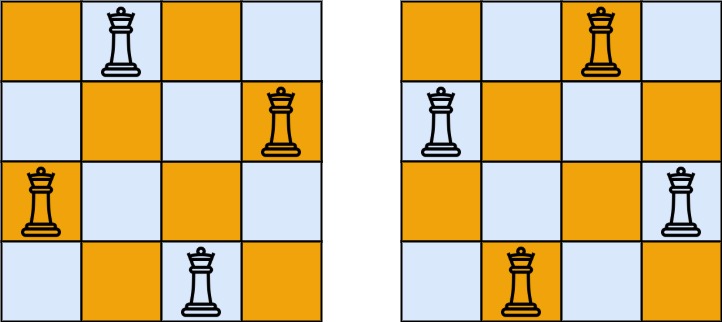
输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

示例 2：

输入：n = 1
输出：[["Q"]]

提示：

1 <= n <= 9

二、解题思路

初始化一个 n x n 的棋盘，每个位置初始为 '.'。
使用递归回溯的方法尝试在每一行放置一个皇后。
在尝试放置皇后时，检查是否有冲突（即该位置是否在之前放置的皇后的攻击范围内，包括同一行、同一列以及两个对角线）。
如果在某一行找不到合适的位置放置皇后，则回溯到上一行。
当所有行都成功放置了皇后后，记录当前棋盘的状态为一个解。
继续递归搜索，直到找到所有可能的解。

三、具体代码

import java.util.ArrayList;
import java.util.List;

class Solution {
    public List<List<String>> solveNQueens(int n) {
        List<List<String>> solutions = new ArrayList<>();
        List<Integer> columns = new ArrayList<>(); // 用于记录每行皇后的列位置
        char[][] board = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                board[i][j] = '.';
            }
        }
        backtrack(board, solutions, columns, 0);
        return solutions;
    }

    private void backtrack(char[][] board, List<List<String>> solutions, List<Integer> columns, int row) {
        if (row == board.length) {
            // A solution is found, add it to the solutions list
            solutions.add(convertBoardToStringList(board));
            return;
        }
        for (int col = 0; col < board.length; col++) {
            if (isValid(board, columns, row, col)) {
                columns.add(col); // 将当前皇后的列位置添加到列表中
                board[row][col] = 'Q'; // 放置皇后
                backtrack(board, solutions, columns, row + 1); // 递归放置下一行的皇后
                columns.remove(columns.size() - 1); // 回溯，移除当前皇后的列位置
                board[row][col] = '.'; // 移除皇后，回溯
            }
        }
    }

    private boolean isValid(char[][] board, List<Integer> columns, int row, int col) {
        // Check if the current position is under attack
        for (int i = 0; i < row; i++) {
            if (board[i][col] == 'Q' || columns.contains(col)) {
                return false; // 同一列或同行已有皇后
            }
            // Check upper diagonal
            int diag1 = col - (row - i);
            if (diag1 >= 0 && board[i][diag1] == 'Q') {
                return false;
            }
            // Check lower diagonal
            int diag2 = col + (row - i);
            if (diag2 < board.length && board[i][diag2] == 'Q') {
                return false;
            }
        }
        return true;
    }

    private List<String> convertBoardToStringList(char[][] board) {
        List<String> boardStr = new ArrayList<>();
        for (int i = 0; i < board.length; i++) {
            StringBuilder sb = new StringBuilder();
            for (int j = 0; j < board[i].length; j++) {
                sb.append(board[i][j]);
            }
            boardStr.add(sb.toString());
        }
        return boardStr;
    }
}

四、时间复杂度和空间复杂度

1. 时间复杂度

回溯算法的时间复杂度通常较难直接计算，因为它依赖于问题的解空间结构。在 n 皇后问题中，我们需要在 n 行中每行放置一个皇后，且皇后之间不能相互攻击。
对于每一行，我们有 n 个可能的位置来放置皇后。因此，如果我们不考虑冲突检查，最坏情况下的尝试次数是 n^n。
然而，由于皇后不能攻击同一行、同一列或对角线上的其他皇后，实际尝试次数会少得多。每次递归调用都会减少一个可行的选择，因此时间复杂度大致为 O(n!)，因为每一步都需要检查当前位置是否安全，这需要 O(n) 的时间。
但是，由于我们在每一行放置皇后时都会剪枝（即跳过不符合条件的位置），实际的时间复杂度通常要好于 O(n!)。具体的时间复杂度取决于剪枝的效率。

2. 空间复杂度

空间复杂度主要由棋盘的大小和递归栈的深度决定。
棋盘是一个 n x n 的二维数组，因此空间复杂度为 O(n^2)。
递归栈的深度最坏情况下可以达到 n，因为我们需要递归 n 次来放置 n 个皇后。此外，我们在递归过程中使用了一个 columns 列表来存储每行皇后的列位置，这个列表的长度最多为 n。
因此，总的空间复杂度为 O(n^2 + n)，其中 n^2 是棋盘的空间占用，n 是递归栈和 columns 列表的空间占用。通常，我们关注最坏情况下的空间复杂度，所以可以表示为 O(n^2)。

请注意，尽管这个算法的时间复杂度可能看起来很高，但实际上由于有效的剪枝，它通常能够在合理的时间内找到所有解。