审题
第四问让我们探究性别比例变化是否对生态系统中的其他生物如寄生虫提供优势。这里我们可以把问题简化一下,只探究性别比例会不会对寄生虫提供优势。因为考虑太多生物,会使模型更复杂,我这个水平处理不了这么复杂的问题,是我太菜了。
既然已经把问题简化了,接下来就是研究寄生虫有什么特性,七鳃鳗和寄生虫是什么关系,进一步研究出性别比例能否为寄生虫提供优势。
这道题里我们认为寄生虫是寄生在七鳃鳗上的,七鳃鳗是寄生虫的宿主。
然后我们通过查论文发现,寄生虫比较喜欢寄生在雌性个体上,而且寄生虫对宿主的致死率不能太高,否则寄生虫自身的种群的数量也会降低。寄生虫的数量与宿主的数量是关联的,一个宿主身上不能寄生无限多的寄生虫。
搞明白了寄生虫和宿主的关系,接下来就是建立寄生虫的种群增长模型了,套路和之前的问题都一样。只是这里因为寄生虫的数量和宿主的数量是关联的,所以我们要联立七鳃鳗和寄生虫的之前增长模型。
建模
七鳃鳗种群增长模型,这一问的模型和之前的七鳃鳗模型有一点区别,因为考虑了七鳃鳗作为宿主的情况。

这里x1是七鳃鳗的种群数量,x2是寄生虫的种群数量,r1 是七鳃鳗的自然增长率,K是七鳃鳗的最大种群数量,alpha是雄性占比,d2是寄生虫的感染致死率。因为寄生虫会导致宿主死亡,并且我们要考虑性别比例对寄生虫数量的影响,这里有个 - alpha * d2 * x2。
寄生虫的种群增长模型。
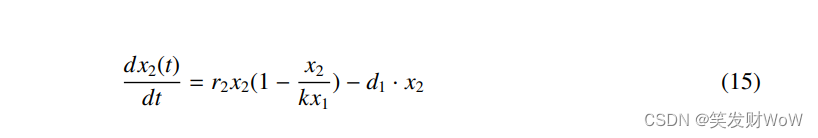
这里x1是七鳃鳗的种群数量,x2是寄生虫的种群数量。r2是寄生虫的自然增长率,d1是寄生虫的自然死亡率。k是一个宿主上能寄生多少寄生虫的数量。因为一个宿主身上不能寄生无限多的寄生虫,所以寄生虫的数量受到k * x1的约束。
联立方程

这里设初始x1为100,x2为10。带入方程进行计算。

建模结果
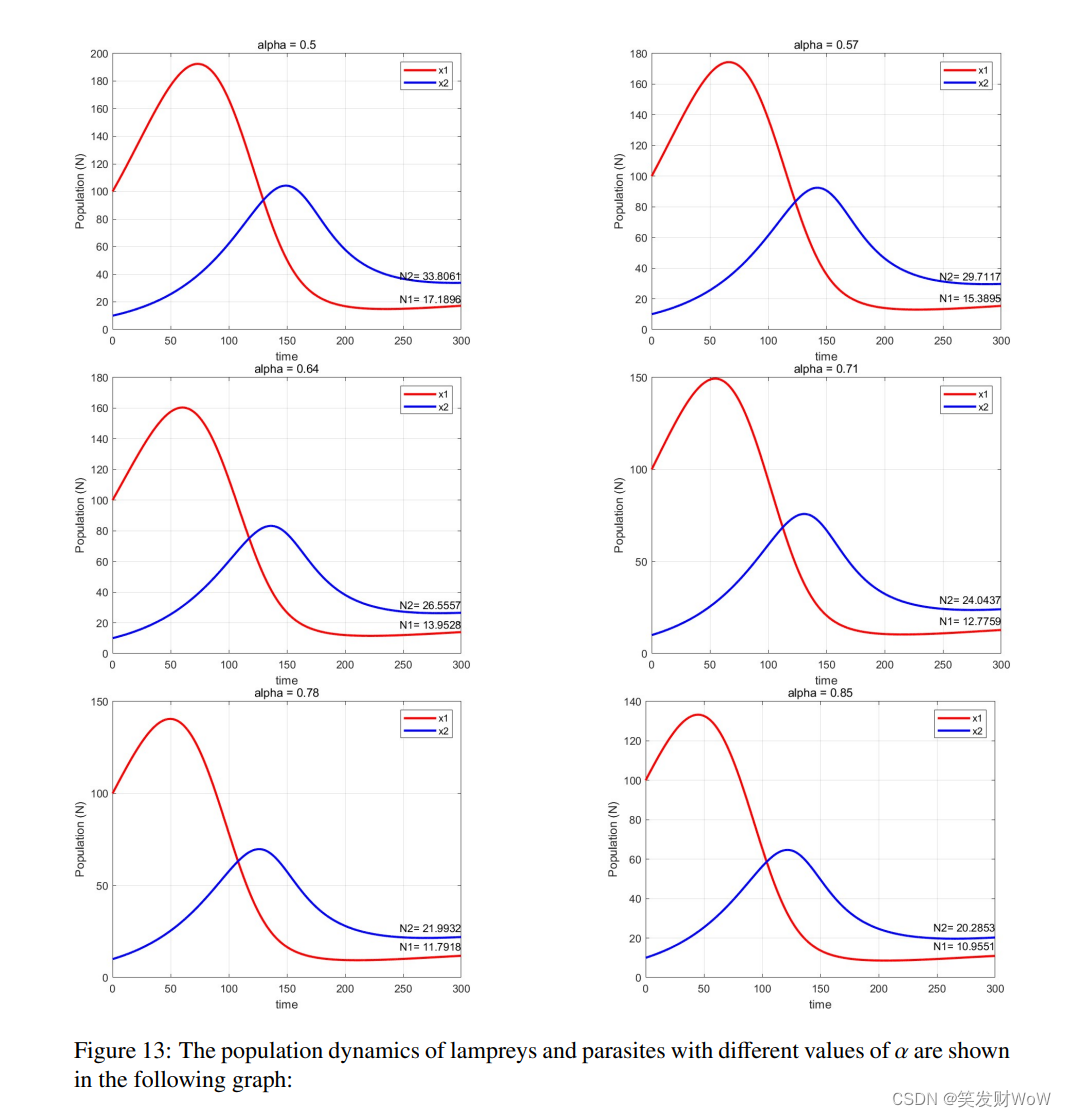
从结果可以看到,确实当雄性占比越少,雌性占比越多时,寄生虫的数量越多,符合我们之前找的资料。说明性别比例可以为寄生虫提供优势。当然这张图还有很多可以分析的点,我就是不写了,主要是我忘得也差不多了。
灵敏度分析
在这个模型中的参数都是我们自己定的。所以我们还要探究我们设定的参数是否对模型有影响,影响大不大。这时就需要灵敏度分析。也就是探究在参数不同时,结果有说明变化。
我们探究了r1,r2,d1,d2不同时,模型计算的结果如下。



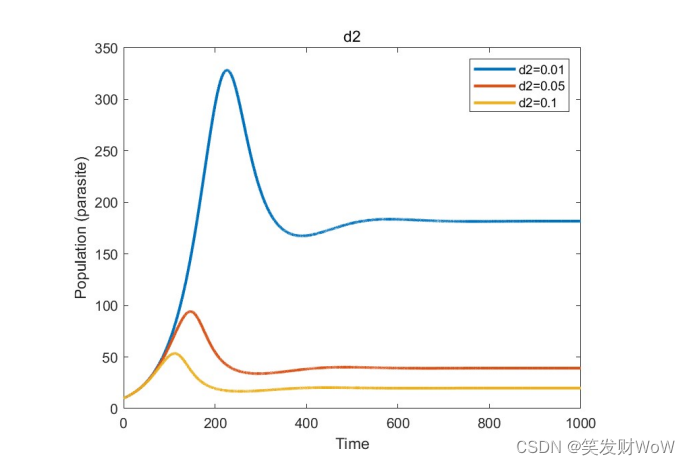
可以看到r1对结果的影响比较小,其他参数对结果的影响比较大。这里也有很多细节的点可以分析,我懒得写了。
代码
fun.m
function dx=fun(t,x,r1,r2,n1,n2,s1,s2)
r1=0.02;%增长率
r2=0.03;%感染率
n1=1000;%鳗鱼种群最大值
d1 = 0.01;%死亡率
d2 = 0.1;%感染致死率
alpha = 0.50;%性别比例
x1 = r1 * x(1) *(1-x(1)/n1 - alpha * d2 * x(2)) ;
x2 = r2 * x(2) *(1-x(2)/(3 * x(1))) - d1 * x(2);
dx=[x1;
x2];
endrun.m
h=0.1;%所取时间点间隔
ts=[0:h:1000];%时间区间
x0=[100,10];%初始条件
opt=odeset('reltol',1e-6,'abstol',1e-9);%相对误差1e-6,绝对误差1e-9
[t,x]=ode45(@fun,ts,x0,opt);%使用5级4阶龙格—库塔公式计算
% subplot(2,1,1);
plot(t,x(:,1),'r',t,x(:,2),'b','LineWidth',2),grid;
legend('x1','x2');
xlabel('time');
ylabel('Population (N)')
title('r = 0.03')
text(t(end), x(end,1)+5, ['N1= ', num2str(x(end,1))], 'HorizontalAlignment', 'right');
text(t(end), x(end,2)+5, ['N2= ', num2str(x(end,2))], 'HorizontalAlignment', 'right');
% subplot(2,1,2);
% plot(x(:,1),x(:,2),'LineWidth',2),grid %作相轨线