1. 题目解析

题目地址：点这里

2. 讲解算法原理

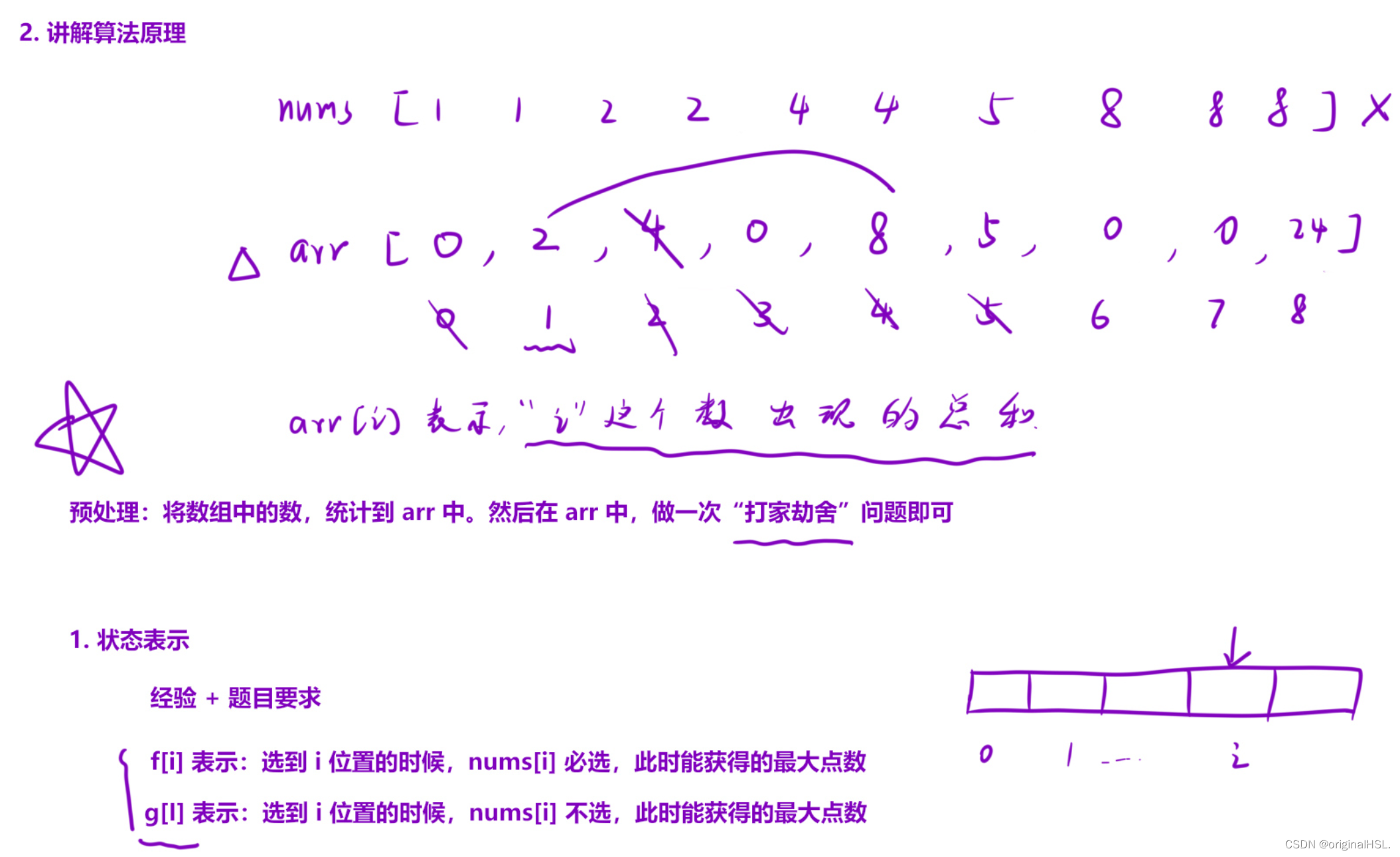
1. rob_s函数：这个函数实现了经典的"打家劫舍"问题的算法。使用动态规划的思想，通过填表的方式计算在给定范围内能够获取的最大点数。

   • f和g分别是两个辅助数组，其中f[i]表示选择第i个数字后能够获取的最大点数，g[i]表示不选择第i个数字能够获取的最大点数。
   • 初始化第一个数字的情况：f[left] = nums[left]表示选择第一个数字后的最大点数为该数字本身，g[left] = 0表示不选择第一个数字的最大点数为0。
   • 从left + 1开始，逐个计算每个数字的最大点数。对于第i个数字，有两种选择：选择第i个数字，则最大点数为不选择第i-1个数字的最大点数加上该数字的点数；不选择第i个数字，则最大点数为选择或不选择第i-1个数字的最大点数中的较大值。
   • 最终返回最后一个数字的最大点数，即为在给定范围内能够获取的最大点数。

2. deleteAndEarn函数：这个函数实现了"删除与获得点数"问题的解决方案。

   • 创建一个大小为10001的数组arr，用于统计每个数字出现的次数，并将其乘以数字本身，以便后续在"打家劫舍"问题中使用。
   • 循环遍历nums数组中的每个数字，统计其出现的次数。
   • 将统计结果乘以数字本身，即将arr[i]设置为数字i的点数乘以出现次数。
   • 调用rob_s函数，将范围设置为0到10000，传入arr数组进行计算，得到在给定范围内能够获取的最大点数。

3. 编写代码

class Solution {
public:
    //打家劫舍
    int rob_s (int left,int right,vector<int>&nums)
    {
        int n=nums.size();
        vector<int> f(n);
        vector<int> g(n);
        f[left]=nums[left],g[left]=0;
        for(int i=left+1;i<=right;i++)
        {
            f[i]=g[i-1]+nums[i];
            g[i]=max(g[i-1],f[i-1]);
        }
        return max(f[right],g[right]);
    }

    int deleteAndEarn(vector<int>& nums) {
        vector<int> arr(10001);
        for(auto e:nums)arr[e]++;
        for(int i=0;i<10001;i++)
        {
            arr[i]=i*arr[i];
        }
        //for(auto x:nums) arr[x]+=x;
        return rob_s(0,10000,arr);
    }
};