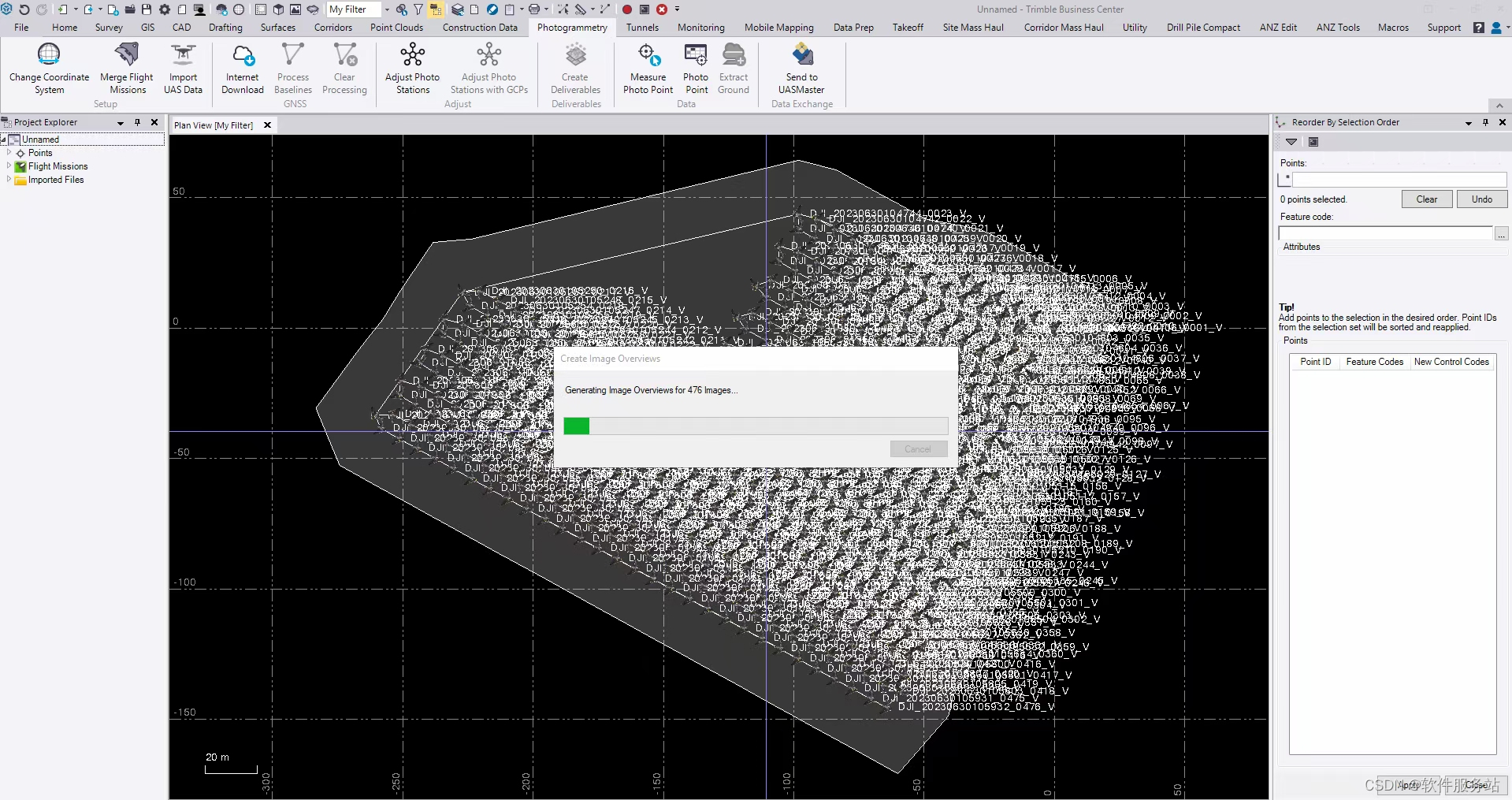
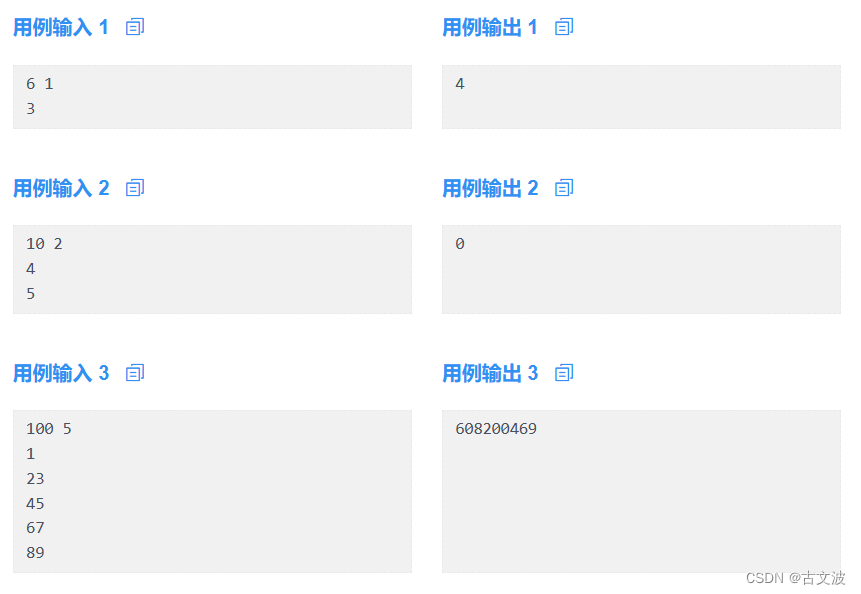
题目描述

有一个有 N 级台阶的楼梯。高桥现在站在楼梯的脚下，也就是第0个台阶上。他可以一次爬上一个或两个台阶。

但是，编号为a[1] ~ a[m]台阶的踏板都坏了，所以踏上这些台阶很危险。

在不踏上坏掉的台阶的情况下，有多少中方案可以爬到最上面的台阶，也就是第N个台阶？求模数1000000007。

输入描述

N M
a[1]
a[2]
……
a[m]

输出描述：

打印在条件下爬楼梯的方式数，模数为 1 000 000 007。

思路：

首先，在台阶都没问题的话，$a[n]=a[n-1]+a[n-2]$，这个是递推关系式
但是现在有一些台阶坏了，所以我们就这样做：
如果这个台阶坏了，跳过不算；
否则，$a[n]=a[n-1]+a[n-2]$即可

参考代码：

#include <bits/stdc++.h>

using namespace std;

const int mod = 1e9 + 7;

int n, m;
int a[100007];
bool f[100007];
int x;

int main() {
    cin >> n >> m;
    for(int i = 1; i <= m; i++) {
        cin >> x;
        f[x] = true;
    }
    a[0] = 1;
    if(!f[1]) a[1] = 1;
    for(int i = 2; i <= n; i++) {
        if(f[i]) continue;
        a[i] = (a[i - 1] + a[i - 2]) % mod;
    }
    cout << a[n];
}