在结点上给出结点基函数，接着做该基函数的线性组合，组合的系数为结点的函数值,这种插值多项式称为拉格朗日插值公式。通俗地说，就是通过平面上的两个点确定一条直线。该插值方法是一种较为基础的方法，同时该方法也较容易理解与实现。

拉格朗日插值多项式的表达式为:

其中，li(x)称为i次的基函数。且li(x)的表达式为:

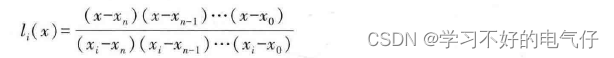
结合以上两式可得拉格朗日插值多项式的表达式为:

在MATLAB中，没有可以实现拉格朗日插值的专门函数，根据以上对拉格朗日插值公式的介绍，可以自行创建该插值函数。

例:拉格朗日插值函数的编写与实现

1）创建M文件，输入以下代码并保存。

function yh= test4(x,y ,xh)

n=length(x);

m=length(xh);

yh =zeros( 1,m);

cl=ones(n-1,1);

c2=ones(1,m);

for i=l:n

xp=x([1:i-1 i+1:n]);

yh =yh+y(i) prod((cl * xh-xp ' *c2)./(x(i)-xp'* c2));

end

2)输入以下代码，即可实现插值。

>>x=[1 2 3 4 5 6];

y=[24 45 67 168 310 412];

xh=4.5;

test4(x,y,xh)

ans =

238.7852