java子集（力扣Leetcode78）

news2024/10/9 16:24:52

子集

力扣原题链接

问题描述

给定一个整数数组 nums，数组中的元素互不相同。返回该数组所有可能的子集（幂集）。解集不能包含重复的子集。可以按任意顺序返回解集。

示例

示例 1：

输入：nums = [1,2,3]
输出：[[],[1],[2],[1,2],[3],[1,3],[2,3],[1,2,3]]

示例 2：

输入：nums = [0]
输出：[[],[0]]

解题思路

这是一个典型的回溯算法问题，需要找出给定数组的所有可能子集。我们可以通过递归回溯的方法来解决。

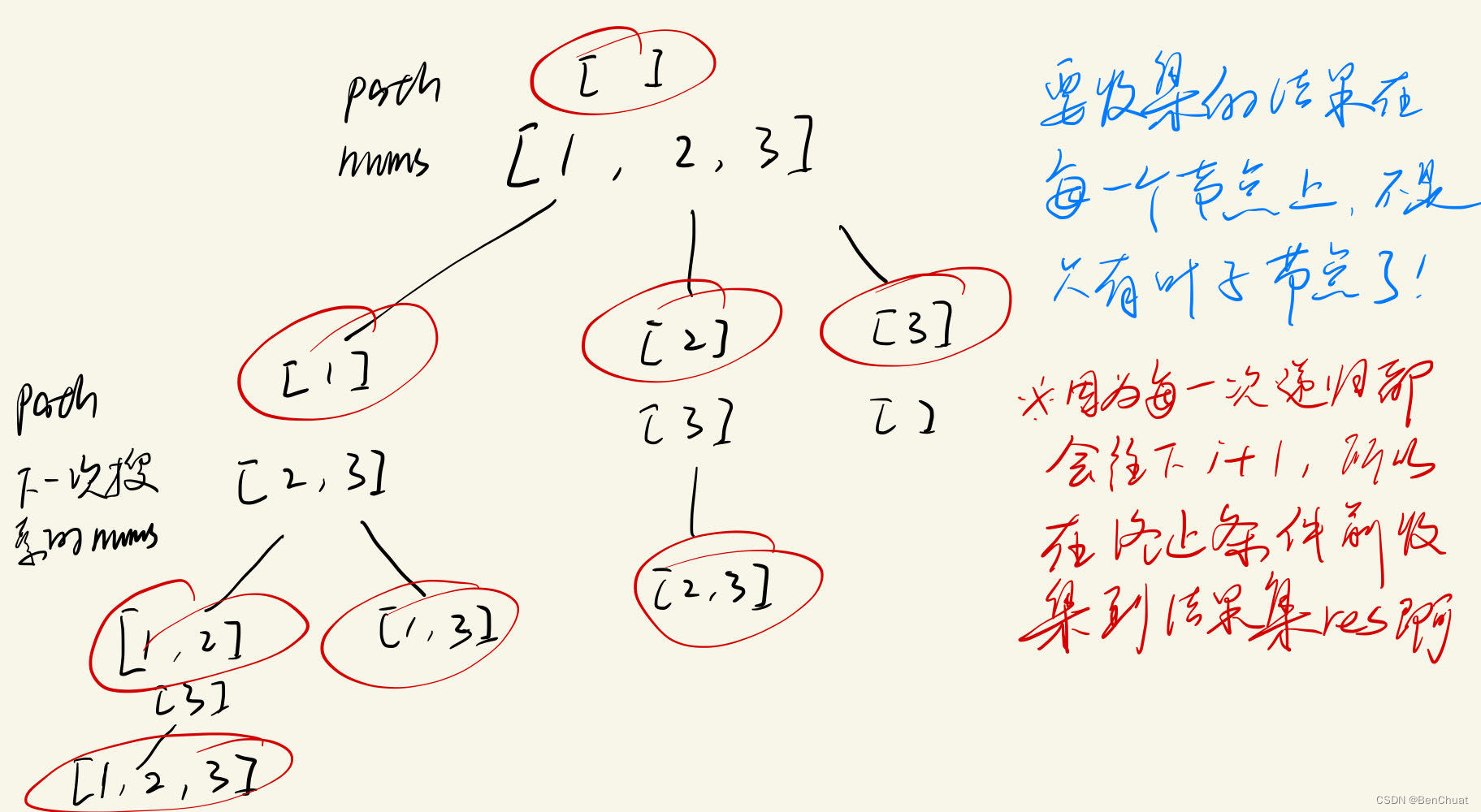
初始化结果列表： 定义一个列表 res 用于存储所有可能的子集。
回溯搜索： 定义一个回溯函数 backtrack，其参数包括当前处理的索引 start、当前已形成的子集 path。
将当前子集加入结果列表： 在每次递归调用回溯函数之前，将当前子集 path 加入结果列表 res。
结束条件： 当 start 等于数组长度时，表示已处理完所有元素，结束当前递归。
选择列表： 对于当前索引 start，我们有两种选择：选择当前元素加入子集，或者不选择当前元素。
递归进入下一层： 如果选择当前元素，则将当前元素加入子集 path，并递归调用回溯函数，传入更新后的索引 i + 1 和子集 path。
撤销选择： 回溯到上一层时，需要撤销当前选择，即将当前元素从子集 path 中移除，然后尝试不选择当前元素的情况，递归调用回溯函数。

请添加图片描述

Java解题

写法一

class Solution {
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        backtrack(nums, 0, new ArrayList<Integer>());
        return res;
    }

    public void backtrack(int[] nums, int start, List<Integer> path) {
        res.add(new ArrayList<>(path)); // 将当前子集加入结果列表
        if (start == nums.length) return; // 结束条件

        // 选择当前元素加入子集，并递归进入下一层
        for (int i = start; i < nums.length; i++) {
            path.add(nums[i]);
            backtrack(nums, i + 1, path);
            path.remove(path.size() - 1); // 撤销选择
        }
    }
}

写法二

class Solution {
    List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        List<Integer> subset = new ArrayList<>();
        backtrack(nums, 0, subset);
        return res;
    }

    public void backtrack(int[] nums, int index, List<Integer> subset) {
        // 结束条件：已处理完所有元素，将当前子集加入结果列表
        if (index == nums.length) {
            res.add(new ArrayList<>(subset));
            return;
        }
        // 选择当前元素加入子集，并递归进入下一层
        subset.add(nums[index]);
        backtrack(nums, index + 1, subset);
        // 撤销选择，不选择当前元素，并递归进入下一层
        subset.remove(subset.size() - 1);
        backtrack(nums, index + 1, subset);
    }
}