AVL树深度解析

news2024/10/9 18:20:38

目录

一.   AVL树的概念

二.   AVL树节点的定义

三.   AVL树的基本操作

3.1   插入操作：

3.1.1   parent->_pf = 0

3.1.2   abs(parent->_pf) = 1

3.1.3   abs(parent->_pf) = 2

3.1.3.1        parent->_pf = 2 && cur->_pf = 1  

3.1.3.2        parent->_pf = -2 && cur->_pf =- 1

3.1.3.3        parent->_pf = -2 && cur->_pf = 1

3.1.3.4        parent->_pf = 2 && cur->_pf = -1

四.   总体代码

一.   AVL树的概念

我们上一篇博客讲了，二叉搜索树在极端情况下会退化为单支树的情况（具体可以看上一篇博客：）。那我们该如何解决这种问题呢？

诶，还真有这种方法，是由著名的两位俄罗斯的数学家G.M.Adelson-Velskii和E.M.Landis在1962年提出的。如果让左右子树的高度差的绝对值不超过1，那我们就可以避免这种单支树的情况。

那我们将具有以下特征的二叉搜索树叫做AVL树：

  1. 左右子树的高度差（这里简称平衡因子）的绝对值不超过1
  2. 左右子树都是AVL树

 

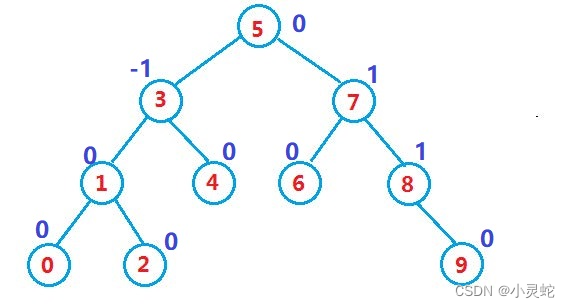
 如果一棵树是高度平衡的，那它就是AVL树，如果这棵树有n个节点，那我们能把这棵树的高度维持在log2n，查找的时间复杂度可以维持在O(log2n)。

二.    AVL树节点的定义

我们用代码来刻画这个定义：

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _pf;//平衡因子
	pair<K, V> _kv;
	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_pf(0)
		,_kv(kv)
	{}
};

可以看见，我们引进了平衡因子这个变量，来显示左右子树的高度差。

特别说明：此处平衡因子是右边减去左边。

三.   AVL树的基本操作

我们这里着重讲解AVL树的插入操作，其他操作与普通的二叉搜索树是一样的。

3.1   插入操作：

bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur=_root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first>kv.first)
		{
			parent->_left = cur;
		}
		else if(parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		cur->_parent = parent;
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_pf--;
			}
			else if (cur == parent->_right)
			{
				parent->_pf++;
			}
			if (parent->_pf == 0)
			{
				break;
			}
			else if (parent->_pf == 1 || parent->_pf == -1)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_pf == 2 || parent->_pf == -2)
			{
				//旋转处理
				if (parent->_pf == 2 && cur->_pf == 1)
				{
					RotaleL(parent);
				}
				else if (parent->_pf == -2 && cur->_pf ==- 1)
				{
					RotaleR(parent);
				}
				else if (parent->_pf == -2 && cur->_pf == 1)
				{
					RotaleLR(parent);
				}
				else
				{
					RotaleRL(parent);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}

我们依次来解析需要特殊处理的情况：

3.1.1   parent->_pf = 0

当父节点的平衡因子为0时，证明左右子树是平衡的，不需要再做处理，直接跳出循环。

if (parent->_pf == 0)
{
	break;
}

3.1.2   abs(parent->_pf) = 1

当父节点的平衡因子的绝对值为1时，证明此父节点下的子树是平衡的，但是，由于我们前面改变了父节点的平衡因子，可能导致父节点的祖宗节点不平衡，所以我们要向上迭代，再次进行判断。

else if (parent->_pf == 1 || parent->_pf == -1)
{
	cur = cur->_parent;
	parent = parent->_parent;
}

3.1.3   abs(parent->_pf) = 2

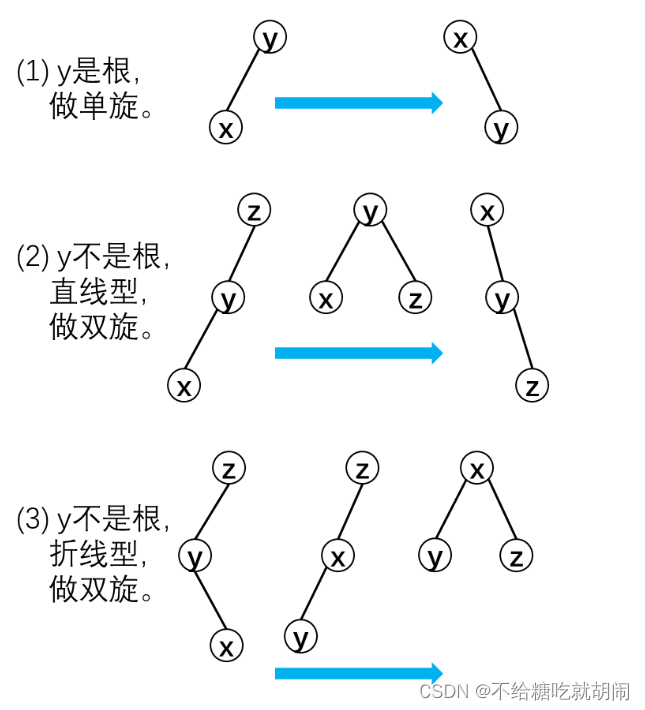
当父节点的平衡因子绝对值为2时，我们为了保证树的平衡，需要进行一些旋转操作。此类情况比较复杂，又细分为以下几种情况：

3.1.3.1        parent->_pf = 2 && cur->_pf = 1  

当父节点的平衡因子为2，而当前节点平衡因子为1时，是在当前节点是父节点的右子节点，并且插入节点是当前节点的右子节点发生的。

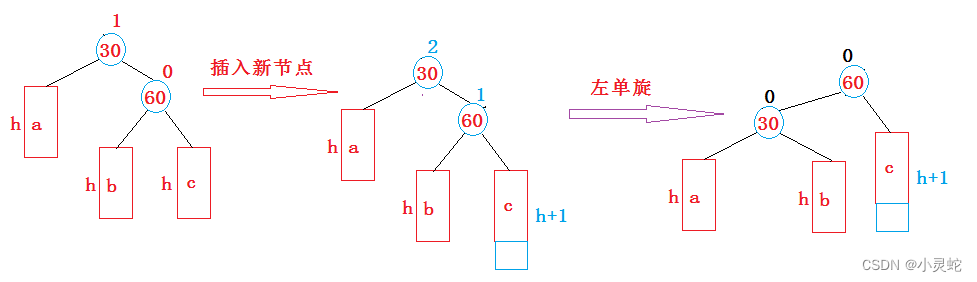
此时我们要进行左单旋：

if (parent->_pf == 2 && cur->_pf == 1)
{
	RotaleL(parent);
}

void RotaleL(Node* parent)
{
	totalSize++;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	parent->_right = subRL;
	subR->_left = parent;
	if (subRL)
	{
		subRL->_parent = parent;
	}
	Node* ppnode = parent->_parent;
	parent->_parent = subR;
	if (parent == _root)
	{
		_root = subR;
		subR->_parent == nullptr;
	}
	else
	{
		if (parent == ppnode->_left)
		{
			ppnode->_left = subR;
		}
		else if (parent == ppnode->_right)
		{
			ppnode->_right = subR;
		}
		subR->_parent = ppnode;
	}
	parent->_pf = 0;
	subR->_pf = 0;
}

 总结来说，此情况就是让当前节点的左子树变为父节点的右子树，而当前节点的左子树变为父节点，再改变当前节点和父节点的父节点指向并更新平衡因子即可。

3.1.3.2        parent->_pf = -2 && cur->_pf =- 1

当父节点的平衡因子为-2，而当前节点平衡因子为-1时，是在当前节点是父节点的左子节点，并且插入节点是当前节点的左子节点发生的。

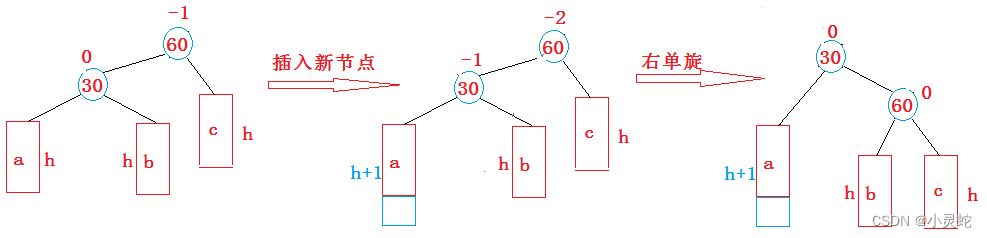
此时我们要进行右单旋：

else if (parent->_pf == -2 && cur->_pf ==- 1)
{
	RotaleR(parent);
}

void RotaleR(Node* parent)
{
	totalSize++;
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	parent->_left = subLR;
	if (subLR)
	{
		subLR->_parent = parent;
	}
	subL->_right = parent;
	Node* ppnode = parent->_parent;
	parent->_parent = subL;
	if (parent == _root)
	{
		_root=subL;
		subL->_parent = nullptr;
	}
	else
	{
		if (ppnode->_left == parent)
		{
			ppnode->_left = subL;
		}
		else if (ppnode->_right == parent)
		{
			ppnode->_right = subL;
		}
		subL->_parent = ppnode;
	}
	subL->_pf = 0;
	parent->_pf = 0;
}

总结来说，此情况就是让当前节点的右子树变为父节点的左子树，而当前节点的右子树变为父节点，再改变当前节点和父节点的父节点指向并更新平衡因子即可。

3.1.3.3        parent->_pf = -2 && cur->_pf = 1

 当父节点的平衡因子为-2，而当前节点平衡因子为1时，是在当前节点是父节点的左子节点，并且插入节点是当前节点的右子节点发生的。

 

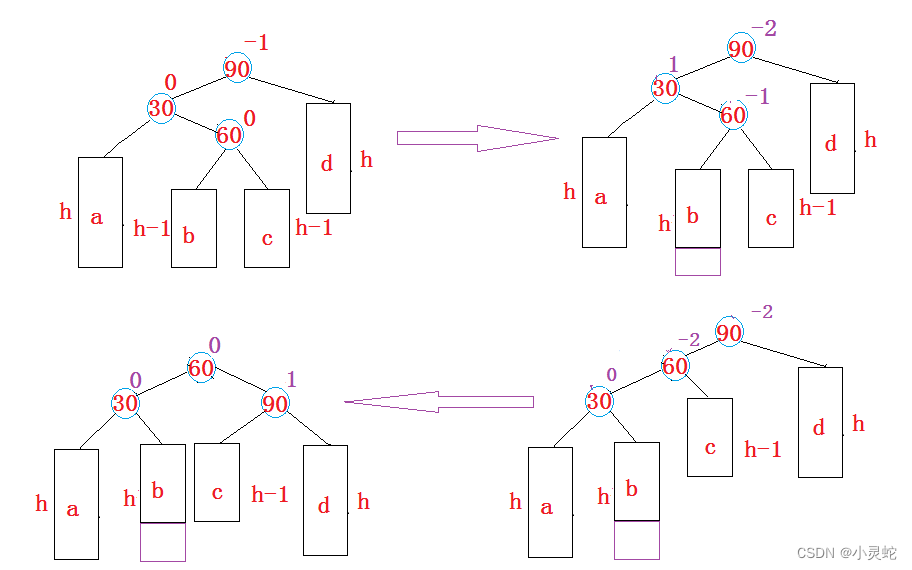
此情况比较复杂，单一的旋转已经不能满足树的平衡了，我们此时要先左旋再右旋：

else if (parent->_pf == -2 && cur->_pf == 1)
{
	RotaleLR(parent);
}

void RotaleLR(Node* parent)
{
	totalSize++;
	Node* subL = parent->_left;
	Node* subLR = subL->_right;
	int pf = subLR->_pf;
	RotaleL(parent->_left);
	RotaleR(parent);
	if (pf == 1)
	{
		subLR->_pf = 0;
		subL->_pf = -1;
		parent->_pf = 0;
	}
	else if (pf == -1)
	{
		subL->_pf = 0;
		subLR->_pf = 0;
		parent->_pf = 1;
	}
	else if (pf == 0)
	{
		subL->_pf = 0;
		subLR->_pf = 0;
		parent->_pf = 0;
	}
}

总结来说，可以复用前面的左旋与右旋函数，但是与前面不同的是需要分情况处理平衡因子。

3.1.3.4        parent->_pf = 2 && cur->_pf = -1

当父节点的平衡因子为2，而当前节点平衡因子为-1时，是在当前节点是父节点的右子节点，并且插入节点是当前节点的左子节点发生的。

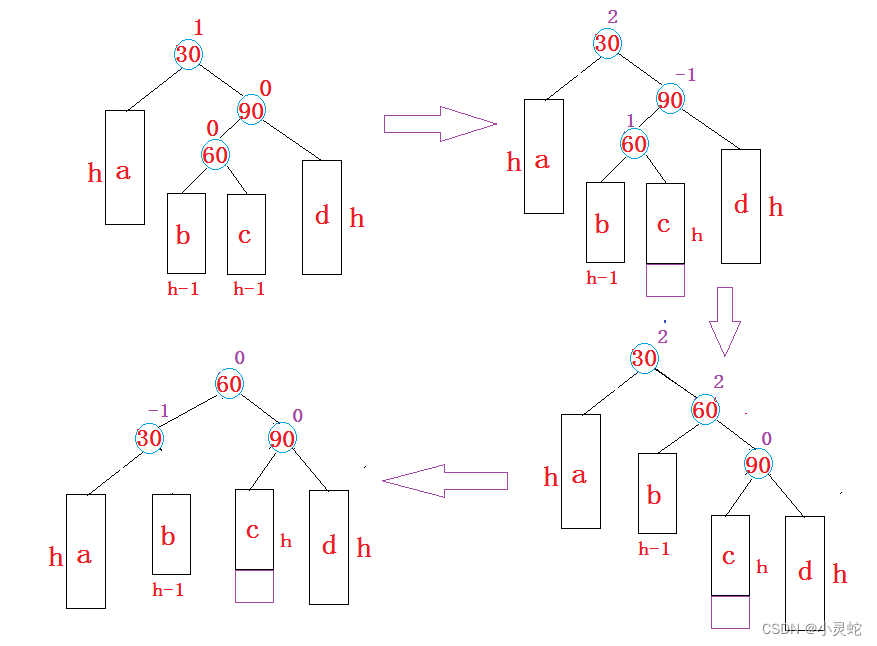
此情况同样单一的旋转已经不能满足树的平衡了，我们此时要先右旋再左旋： 

else
{
	RotaleRL(parent);
}

void RotaleRL(Node* parent)
{
	totalSize++;
	Node* subR = parent->_right;
	Node* subRL = subR->_left;
	int pf = subRL->_pf;
	RotaleR(parent->_right);
	RotaleL(parent);
	if (pf == 1)
	{
		subRL->_pf = 0;
		subR->_pf = 0;
		parent->_pf = -1;
	}
	else if (pf == -1)
	{
		subR->_pf = 1;
		subRL->_pf = 0;
		parent->_pf = 0;
	}
	else if (pf == 0)
	{
		subR->_pf = 0;
		subRL->_pf = 0;
		parent->_pf = 0;
	}
}

总结来说，可以复用前面的右旋与左旋函数，但是与前面同样不同的是需要分情况处理平衡因子。

四.   总体代码

整合一下代码，如下：

template<class K,class V>
struct AVLTreeNode
{
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _pf;//平衡因子
	pair<K, V> _kv;
	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr)
		,_right(nullptr)
		,_parent(nullptr)
		,_pf(0)
		,_kv(kv)
	{}
};
template<class K, class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool Insert(const pair<K, V>& kv)
	{
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* parent = nullptr;
		Node* cur=_root;
		while (cur)
		{
			if (cur->_kv.first > kv.first)
			{
				parent = cur;
				cur = cur->_left;
			}
			else if (cur->_kv.first < kv.first)
			{
				parent = cur;
				cur = cur->_right;
			}
			else
			{
				return false;
			}
		}
		cur = new Node(kv);
		if (parent->_kv.first>kv.first)
		{
			parent->_left = cur;
		}
		else if(parent->_kv.first < kv.first)
		{
			parent->_right = cur;
		}
		cur->_parent = parent;
		while (parent)
		{
			if (cur == parent->_left)
			{
				parent->_pf--;
			}
			else if (cur == parent->_right)
			{
				parent->_pf++;
			}
			if (parent->_pf == 0)
			{
				break;
			}
			else if (parent->_pf == 1 || parent->_pf == -1)
			{
				cur = cur->_parent;
				parent = parent->_parent;
			}
			else if (parent->_pf == 2 || parent->_pf == -2)
			{
				//旋转处理
				if (parent->_pf == 2 && cur->_pf == 1)
				{
					RotaleL(parent);
				}
				else if (parent->_pf == -2 && cur->_pf ==- 1)
				{
					RotaleR(parent);
				}
				else if (parent->_pf == -2 && cur->_pf == 1)
				{
					RotaleLR(parent);
				}
				else
				{
					RotaleRL(parent);
				}
				break;
			}
			else
			{
				assert(false);
			}
		}
		return true;
	}
	void RotaleL(Node* parent)
	{
		totalSize++;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		parent->_right = subRL;
		subR->_left = parent;
		if (subRL)
		{
			subRL->_parent = parent;
		}
		Node* ppnode = parent->_parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			_root = subR;
			subR->_parent == nullptr;
		}
		else
		{
			if (parent == ppnode->_left)
			{
				ppnode->_left = subR;
			}
			else if (parent == ppnode->_right)
			{
				ppnode->_right = subR;
			}
			subR->_parent = ppnode;
		}
		parent->_pf = 0;
		subR->_pf = 0;
	}
	void RotaleR(Node* parent)
	{
		totalSize++;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		parent->_left = subLR;
		if (subLR)
		{
			subLR->_parent = parent;
		}
		subL->_right = parent;
		Node* ppnode = parent->_parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			_root=subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (ppnode->_left == parent)
			{
				ppnode->_left = subL;
			}
			else if (ppnode->_right == parent)
			{
				ppnode->_right = subL;
			}
			subL->_parent = ppnode;
		}
		subL->_pf = 0;
		parent->_pf = 0;
	}
	void RotaleLR(Node* parent)
	{
		totalSize++;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		int pf = subLR->_pf;
		RotaleL(parent->_left);
		RotaleR(parent);
		if (pf == 1)
		{
			subLR->_pf = 0;
			subL->_pf = -1;
			parent->_pf = 0;
		}
		else if (pf == -1)
		{
			subL->_pf = 0;
			subLR->_pf = 0;
			parent->_pf = 1;
		}
		else if (pf == 0)
		{
			subL->_pf = 0;
			subLR->_pf = 0;
			parent->_pf = 0;
		}
	}
	void RotaleRL(Node* parent)
	{
		totalSize++;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		int pf = subRL->_pf;
		RotaleR(parent->_right);
		RotaleL(parent);
		if (pf == 1)
		{
			subRL->_pf = 0;
			subR->_pf = 0;
			parent->_pf = -1;
		}
		else if (pf == -1)
		{
			subR->_pf = 1;
			subRL->_pf = 0;
			parent->_pf = 0;
		}
		else if (pf == 0)
		{
			subR->_pf = 0;
			subRL->_pf = 0;
			parent->_pf = 0;
		}
	}
	void _Inorder(Node* root)
	{
		if (root == nullptr)
		{
			return;
		}
		_Inorder(root->_left);
		cout << root->_kv.first << "[" << root->_pf << "]" << endl;
		_Inorder(root->_right);
	}
	void Inorder()
	{
		_Inorder(_root);
	}
	int _Height(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		int leftheight = _Height(root->_left);
		int rightheight = _Height(root->_right);
		return leftheight > rightheight ? leftheight + 1 : rightheight + 1;
	}
	int Height()
	{
		return _Height(_root);
	}
	//初始版本
	/*bool _IsBalance(Node* root)
	{
		if (root == nullptr)
		{
			return true;
		}
		int leftheight = _Height(root->_left);
		int rightheight = _Height(root->_right);
		if (abs(leftheight - rightheight) >= 2)
		{
			cout << root->_kv.first << "不平衡" << endl;
			return false;
		}
		else if ((rightheight - leftheight) != root->_pf)
		{
			cout << root->_kv.first << "平衡因子异常" << endl;
			return false;
		}
		return _IsBalance(root->_left) && _IsBalance(root->_right);
	}*/
	bool _IsBalance(Node* root,int& height)
	{
		if (root == nullptr)
		{
			height = 0;
			return true;
		}
		int leftheight = 0, rightheight = 0;
		if (!_IsBalance(root->_left, leftheight)
			||!_IsBalance(root->_right, rightheight))
		{
			return false;
		}
		if (abs(rightheight - leftheight) >= 2)
		{
			cout << root->_kv.first << "不平衡" << endl;
			return false;
		}
		else if ((rightheight - leftheight) != root->_pf)
		{
			cout << root->_kv.first << "平衡因子异常" << endl;
			return false;
		}
		height = leftheight > rightheight ? leftright + 1 : rightheight + 1;
		return true;
	}
	bool IsBalance()
	{
		int height = 0;
		return _IsBalance(_root,height);
	}
	size_t _size(Node* root)
	{
		if (root == nullptr)
		{
			return 0;
		}
		return _size(root->_left) + _size(root->_right) + 1;
	}
	Node* Find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first > key)
			{
				cur = cur->_left;
			}
			else if (cur->_kv.first < key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	size_t size()
	{
		return _size(_root);
	}
	int GettotalSize()
	{
		return totalSize;
	}
private:
	Node* _root = nullptr;
	int totalSize = 0;
};

 总结

好了，到这里今天的知识就讲完了，大家有错误一点要在评论指出，我怕我一人搁这瞎bb，没人告诉我错误就寄了。

祝大家越来越好，不用关注我（疯狂暗示）

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1554559.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

P3369 【模板】普通平衡树（splay 算法）

P3369 【模板】普通平衡树（splay 算法）

题目描述 您需要写一种数据结构&#xff08;可参考题目标题&#xff09;&#xff0c;来维护一些数&#xff0c;其中需要提供以下操作&#xff1a; 插入一个数 x。删除一个数 x&#xff08;若有多个相同的数&#xff0c;应只删除一个&#xff09;。定义排名为比当前数小的数的…
阅读更多...
6、父子组件传参、路由的嵌套、命名视图、路由跳转传参

6、父子组件传参、路由的嵌套、命名视图、路由跳转传参

一、父子组件传参 1、父传子 在父组件的子组件中自定义一个属性在子组件中有一个props属性&#xff0c;用来接收父组件传递的数据,传递的数据不能修改,还可以设置默认值 <!-- 父组件 -->data() {return {flag: false,num:10, //传的参数free:}} <!-- :type1"…
阅读更多...
【JavaScript算法】DOM树层级显示

【JavaScript算法】DOM树层级显示

题目描述&#xff1a; 上述表达式的输出结果为 [DIV] [P, SPAN, P, SPAN] [SPAN, SPAN]直接上代码 let tree document.querySelector(".a"); function traverseElRoot(elRoot) {const result [];function traverse(element, level) {if (!result[level]) {resul…
阅读更多...
【系统架构师】-第15章-面向服务架构设计

【系统架构师】-第15章-面向服务架构设计

面向服务的体系结构 (Service-Oriented Architecture,SOA) 1、应用角度&#xff1a;它着眼于日常的业务应用&#xff0c;并将它们划分为单独的业务功能和流程&#xff0c;即所谓的服务 2、软件基本原理&#xff1a;一个组件模型&#xff0c;它将应用程序的不同功能单元(称为服…
阅读更多...
Python数据分析必备工具——Pandas模块及其应用

Python数据分析必备工具——Pandas模块及其应用

Python数据分析必备工具——Pandas模块及其应用 外部数据的读取文本文件的读取语法示例 电子表格的读取语法示例 数据库数据的读取与操作语法 数据操作数据概述语法 数据筛选语法 数据清洗数据类型语法示例 沉余数据语法示例 异常值的识别与处理缺失值的识别与处理语法示例 数据…
阅读更多...
PHP图床程序优化版：图片外链服务、图床API服务、图片CDN加速与破解防盗链

PHP图床程序优化版：图片外链服务、图床API服务、图片CDN加速与破解防盗链

图片免费上传 支持本地储存、FTP储存、第三方云储存&#xff08;阿里云 OSS、腾讯云 COS、七牛云等&#xff09;。 图片外链加速 一键转换第三方网站的图片外链地址为图床可分享的图片地址&#xff08;支持CDN&#xff09;。 图片解析服务 直接将第三方外链图片地址显示为…
阅读更多...
BSV区块链的应用开发前景——通过标准化来促进创新

BSV区块链的应用开发前景——通过标准化来促进创新

​​发表时间&#xff1a;2024年3月5日 近年来区块链领域的发展日新月异&#xff0c;各种全新的技术和方法论正在迅猛涌现。在这个瞬息万变的环境之中&#xff0c;标准化不仅仅会为开发者们带来便利&#xff0c;同时也促进了应用之间的互操作性&#xff0c;并且推动着生态系统的…
阅读更多...
【机器学习300问】56、什么是自编码器？

【机器学习300问】56、什么是自编码器？

一、什么是自编码器&#xff1f; 自编码器&#xff08;Autoencoder&#xff0c;AE&#xff09;本质是一种特殊的神经网络架构。主要用于无监督学习和特征学习任务。它的目标是通过编码然后解码的过程&#xff0c;学会重构其输入数据&#xff0c;试图还原其原始输入的。 当时我学…
阅读更多...
【探索Linux】—— 强大的命令行工具 P.31（守护进程）

【探索Linux】—— 强大的命令行工具 P.31（守护进程）

阅读导航 引言一、守护进程简介1. 概念2. 特点 二、用C创建守护进程⭕代码✅主要步骤 温馨提示 引言 当谈到计算机系统中运行的特殊进程时&#xff0c;守护进程&#xff08;daemon&#xff09;无疑是一个备受关注的话题。作为在后台默默运行并提供各种服务的进程&#xff0c;守…
阅读更多...
FreeRTOS从代码层面进行原理分析(4 移植)

FreeRTOS从代码层面进行原理分析(4 移植)

FreeRTOS从代码层面进行原理分析(4 移植) 从前 3 篇博客中我们已经搞清楚了最开始对 FreeRTOS 有疑问的前 2 个问题。 1. FreeRTOS 是如何建立任务的呢&#xff1f; 2. FreeRTOS 是调度和切换任务的呢&#xff1f; 3. FreeRTOS 是如何保证实时性呢&#xff1f; 以下就是前三…
阅读更多...
LeetCode：300最长递增子序列 C语言

LeetCode：300最长递增子序列 C语言

300. 最长递增子序列 给你一个整数数组 nums &#xff0c;找到其中最长严格递增子序列的长度。 子序列 是由数组派生而来的序列&#xff0c;删除&#xff08;或不删除&#xff09;数组中的元素而不改变其余元素的顺序。例如&#xff0c;[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子…
阅读更多...
大话设计模式之迪米特法则

大话设计模式之迪米特法则

迪米特法则&#xff0c;也称为最少知识原则&#xff08;Law of Demeter&#xff09;&#xff0c;是面向对象设计中的一个重要原则&#xff0c;其核心思想是降低耦合度、减少对象之间的依赖关系&#xff0c;从而使系统更加灵活、易于维护和扩展。 根据迪米特法则&#xff0c;一…
阅读更多...
Multisim14.0破解安装教程

Multisim14.0破解安装教程

Multisim14.0中文破解版是一款相当优秀的专业化SPICE仿真标准环境&#xff0c;Multisim14.0中文版功能强悍&#xff0c;为用户提供了所见即所得的设计环境、互动式的仿真界面、动态显示元件、具有3D效果的仿真电路、虚拟仪表、分析功能与图形显示窗口等等。Multisim破解版操作简…
阅读更多...
Linux-1.常见指令以及权限理解

Linux-1.常见指令以及权限理解

目录 本节目标 使用 XShell 远程登录 Linux 关于 Linux 桌面 下载安装 XShell 查看 Linux 主机 ip 使用 XShell 登陆主机 XShell 下的复制粘贴 Linux下基本指令 登录Linux服务器 新建多用户 全屏 1.快速认识5~6个命令 2.详细谈论课件的所有指令 01. ls 指令 02…
阅读更多...
Linux 环境安装Nginx—源码和Dokcer两种安装方式

Linux 环境安装Nginx—源码和Dokcer两种安装方式

一、源代码编译安装Nginx 1.下载最新nginx源码 以nginx-1.25.3.tar.gz为例&#xff1a; 可以使用命令(联网)&#xff1a;curl -O http://nginx.org/download/nginx-1.25.3.tar.gz或在官网下载.tar.gz 2.解压缩 tar -zxvf nginx-1.25.3.tar.gz cd nginx-1.25.3/ 3.安装依赖…
阅读更多...
动态菜单设计

动态菜单设计

查询当前用户下的菜单权限 思路&#xff1a;根据用户id 左关联表 查询出对应的菜单选项 查询SQL select distinct-- 菜单表 去除重复记录sys_menu.id,sys_menu.parentId, sys_menu.name from -- 权限表sys_menu-- 角色与权限表 菜单表id 角色菜单表的菜单id left j…
阅读更多...
数据分析之Power BI

数据分析之Power BI

POWER QUERY 获取清洗 POWER PIVOT建模分析 如何加载power pivot 文件-选项-加载项-com加载项-转到 POWER VIEW 可视呈现 如何加载power view 文件-选项-自定义功能区-不在功能区中的命令-新建组-power view-添加-确定 POWER MAP可视地图
阅读更多...
Redis 6.0.8版本下载

Redis 6.0.8版本下载

简介&#xff1a;Java领域优质创作者楠木 分享Java项目、简历模板、学习资料、面试题库 想必大家在下载redis之前已经逛了很多教程了&#xff0c;可能不尽如意&#xff0c;找不到自己的想要的版本。既然刷到了我的这条博客&#xff0c;说明你是幸运的&#xff01; Redis6.0.8的…
阅读更多...
k8s1.28.8版本配置prometheus监控告警

k8s1.28.8版本配置prometheus监控告警

文章目录 官方架构图组件的具体介绍kube-prometheus包含的组件简介&#xff1a;文件存储路径&#xff1a; 结构分析官网自带的一些规则自己总结流程 1-创建规则磁盘使用率报警规则 详解上面rule流程Alertmanagerg查看 2-报警接收器2.1-邮件报警修改Alertmanager配置查看现有的s…
阅读更多...
【深耕 Python】Data Science with Python 数据科学（2）jupyter-lab和numpy数组

【深耕 Python】Data Science with Python 数据科学（2）jupyter-lab和numpy数组

关于数据科学环境的建立&#xff0c;可以参考我的博客&#xff1a;【深耕 Python】Data Science with Python 数据科学&#xff08;1&#xff09;环境搭建 Jupyter代码片段1&#xff1a;简单数组的定义和排序 import numpy as np np.array([1, 2, 3]) a np.array([9, 6, 2, …
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023