目录

猫粮规划

思路： 

接苹果

思路：

魔族密码 

思路： 

最大正方形

思路： 

最大正方形 2

思路： 

奶牛比赛 

​编辑 思路：

---

        

        

猫粮规划

思路： 

 每种食物都有两种状态，记忆化dfs当然可以，但是你是否觉得这个题很想之前讲过的“小A点菜 ”？（【算法每日一练]-动态规划 （保姆级教程 篇2）#尼克的任务 #数楼梯 #小A点菜-CSDN博客）那道题问的是对于那些菜要花光她的钱，一共有多少方案？这道题问的是一个区间罢了，那么既然题目意思都这么像，跑不了解法也基本一致：

还是设置f[i][j]表示遍历i个东西获得j能量对应的方案数，

f[i][j]=f[i-1][j]+f[i-1][j-a[i]]

那么最终直接把符合题意的j全部加起来就行了。代码如下：（注意好初始化就行）

#include <bits/stdc++.h>
using namespace std;
int ans,n,l,r,a[50],f[50][500];
int main(){
	cin>>n>>l>>r;
	for(int i=1;i<=n;i++)cin>>a[i],f[i][0]=1;
	f[0][0]=1;
	for(int i=1;i<=n;i++)
	for(int j=0;j<=r;j++){
		f[i][j]=f[i-1][j];
		if(j-a[i]>=0)f[i][j]+=f[i-1][j-a[i]];
	}
	for(int j=l;j<=r;j++){
		ans+=f[n][j];
	}
	cout<<ans;
}

既然看到转移仅用到了i-1行的数据，那么i放到外面就可以又降一维，变成这样：

    for(int i=1;i<=n;i++)
	for(int j=r;j>=0;j--){
		if(j-a[i]>=0)f[j]+=f[j-a[i]];
	}

就变成了如下的一维解法：

#include <bits/stdc++.h>
using namespace std;
int ans,n,l,r,a[50],f[500];
int main(){
	cin>>n>>l>>r;
	for(int i=1;i<=n;i++)cin>>a[i];f[0]=1;
	for(int i=1;i<=n;i++)
	for(int j=r;j>=a[i];j--){
		f[j]+=f[j-a[i]];
	}
	for(int j=l;j<=r;j++){
		ans+=f[j];
	}
	cout<<ans;
}

        

        

接苹果

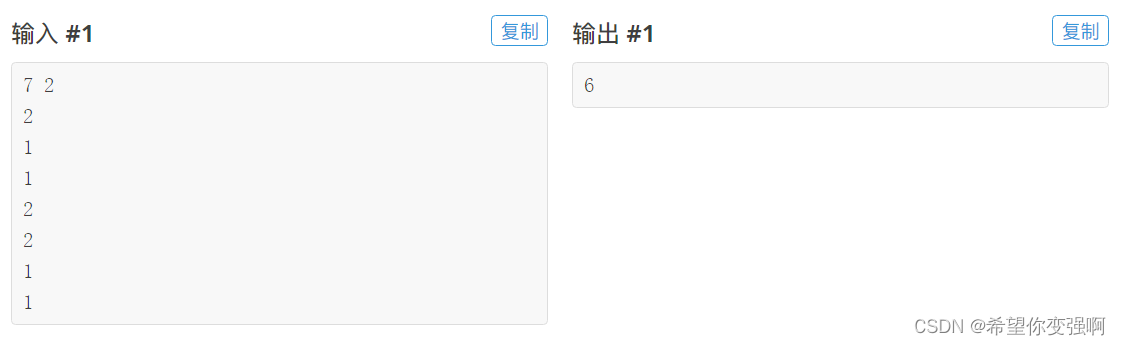
思路：

 还是“小A点菜”的变形题，我们不妨设置1表示站在左边树下，2表示在右边数下。然后设置t表示遍历到了多长时间，j表示已经移动多少次。

然后就出来了：f[i][j][1]表示在第i秒在左边树下当前一件移动j次最多接多少个苹果，f[i][j][2]表示在第i秒在右边树下已经移动j次最多接多少个苹果。然后找关系：

 如果当前左树下掉苹果：有

f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][2])+1;

f[i][j][2]=max(f[i-1][j][2],f[i-1][j-1][1]);

当前在右树下同理。

有两个坑注意一下：

一个是最开始在左边树下，那么j为偶数一定还是在左边，奇数一定是右边

另一个是移动次数最多的不一定是答案！

#include <bits/stdc++.h>
using namespace std;
int ans,t,w,f[1010][50][3],a[1010];
int main(){
	cin>>t>>w;
	for(int i=1;i<=t;i++)cin>>a[i];
	for(int i=1;i<=t;i++)
	for(int j=0;j<=w;j++){
		if(a[i]==1){
			if(j%2==0) f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][2])+1;
			else f[i][j][2]=max(f[i-1][j][2],f[i-1][j-1][1]);
			
		}
		if(a[i]==2){
			if(j%2==1) f[i][j][2]=max(f[i-1][j][2],f[i-1][j-1][1])+1;
			else f[i][j][1]=max(f[i-1][j][1],f[i-1][j-1][2]);
			
		}
	
	}
	for(int i=1;i<=w;i++)
	ans=max(ans,max(f[t][i][1],f[t][i][2]));
	cout<<ans;//不一定移动的次数越多接到的就越多
}

        

        

魔族密码 

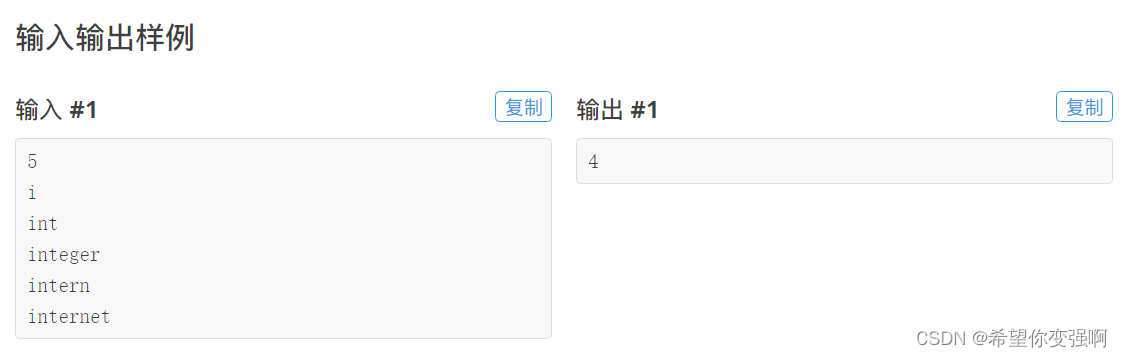
思路： 

注意到词链就是下面的词一定要完全包含前面的，那么不妨把前面的单词看成一个字符，后面多出来的单词也看成一个字符，那就转化成了最长上升子序列了吧。

不过是在转移条件变成了前面的单词时候是后面的前缀。

设置f[i]表示第i个单词结果的词链所包含的最长单词数

f[i]=max(f[j]+1)   j<i      

和最长上升子序列一样，我们的答案不一定是以最后一个字符结尾的，那么就需要都遍历一遍。

补充一下STL：substr(begin,length) 

#include <bits/stdc++.h>
using namespace std;
int n,f[2010],ans;
string s[2010];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++)cin>>s[i];
	for(int i=1;i<=n;i++){
		f[i]=1;
		for(int j=1;j<i;j++){
			if(s[j]==s[i].substr(0,s[j].size()))
				f[i]=max(f[j]+1,f[i]);	
		}
		ans=max(f[i],ans);
	}
	cout<<ans;
}

        

        

最大正方形

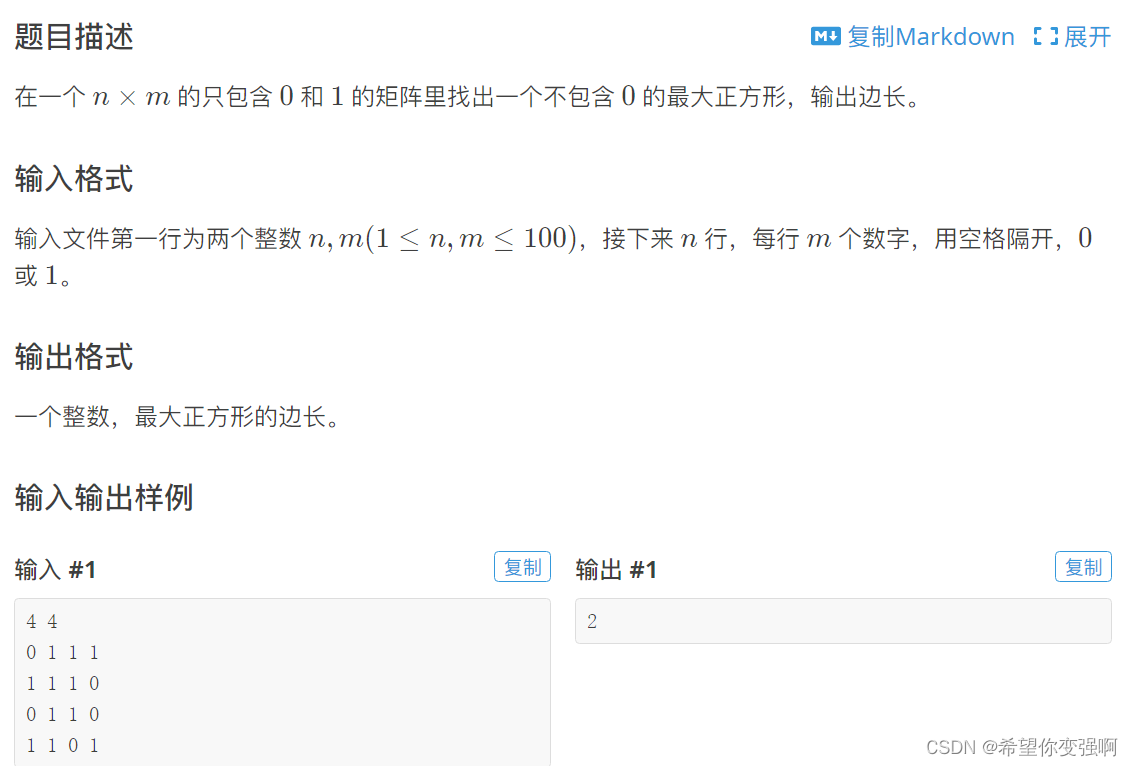
思路： 

这个转移方程还是挺难发现的。

一开始设置f[i][j]表示以<i,j>为右下顶点的不含0的最大正方形，

那么容易发现f[i][j]=min(f[i-1][j],f[i][j-1])+1，然后发现f[i-1][j]一旦为1,就不对了，主要是没有考虑f[i-1][j-1]，那么正确的转移式子应该是：

f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1

注意：
1，不要见到min就把值初始化成iNF，一定要结合f的具体含义
2，其实应该设置每个格子的f初始化值都是1，不过很麻烦，而且我们只需要在转移的时候把这个1加上即可，这样子是等价的。

3，因为每个格子更新一次就会正确，那么就可以直接获取答案

#include <bits/stdc++.h>
using namespace std;
int ans,inf,a[105][105],f[105][105];
int main(){
	int n,m;cin>>n>>m;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++){
		cin>>a[i][j];
		if(a[i][j])f[i][j]=min(min(f[i-1][j],f[i][j-1]),f[i-1][j-1])+1;
		if(f[i][j]!=inf)ans=max(ans,f[i][j]);
	}
	cout<<ans;
}

        

        

最大正方形 2

 

思路： 

如果我们设置f[i][j]表示<i,j>为右下角的最大正方形，因为不清楚<i,j>是0还是1，所以不好转移。

所以设置f[i][j][1]表示<i,j>=1为右下角的最大正方形，f[i][j][0]表示<i,j>=0

f[i][j][1]=min(min(f[i-1][j][0],f[i][j-1][0]),f[i-1][j-1][1])+1;

f[i][j][0]=min(min(f[i-1][j][1],f[i][j-1][1]),f[i-1][j-1][0])+1;

因为每个格子更新一次就会正确，那么就可以直接获取答案

#include <bits/stdc++.h>
using namespace std;
int ans,a[1505][1505],f[1505][1505][2];
int main(){
	int n,m;cin>>n>>m;
	for(int i=1;i<=n;i++)
	for(int j=1;j<=m;j++){
		scanf("%d",&a[i][j]);
		if(a[i][j]) f[i][j][1]=min(min(f[i-1][j][0],f[i][j-1][0]),f[i-1][j-1][1])+1;
		else f[i][j][0]=min(min(f[i-1][j][1],f[i][j-1][1]),f[i-1][j-1][0])+1;
		ans=max(ans,max(f[i][j][0],f[i][j][1]));
	}
	cout<<ans;
}

        

        

奶牛比赛 

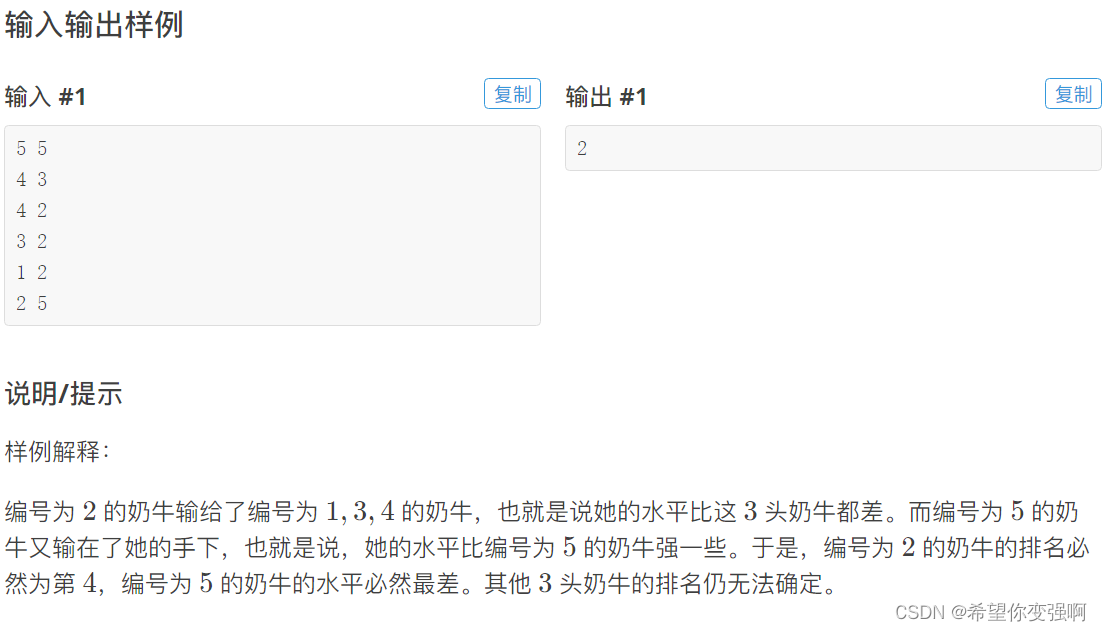 思路：

本题挺考思维的，首先要明确题意：我们可以确定这个点的排名，当且仅当它和其余所有点的关系都已经知道了

我们知道floyd可以通过求最短路来判断两点之间连通性，那么当我们设置f[i][j]为1表示i和j之前有关系，如果u点和任意点都有关系，那么u点就算确定了。

为什么呢？

样例一
5 6
5 2
2 3
2 4
2 1
3 4
4 1
样例二
5 6
5 2
2 3
2 4
2 1
3 4
1 4

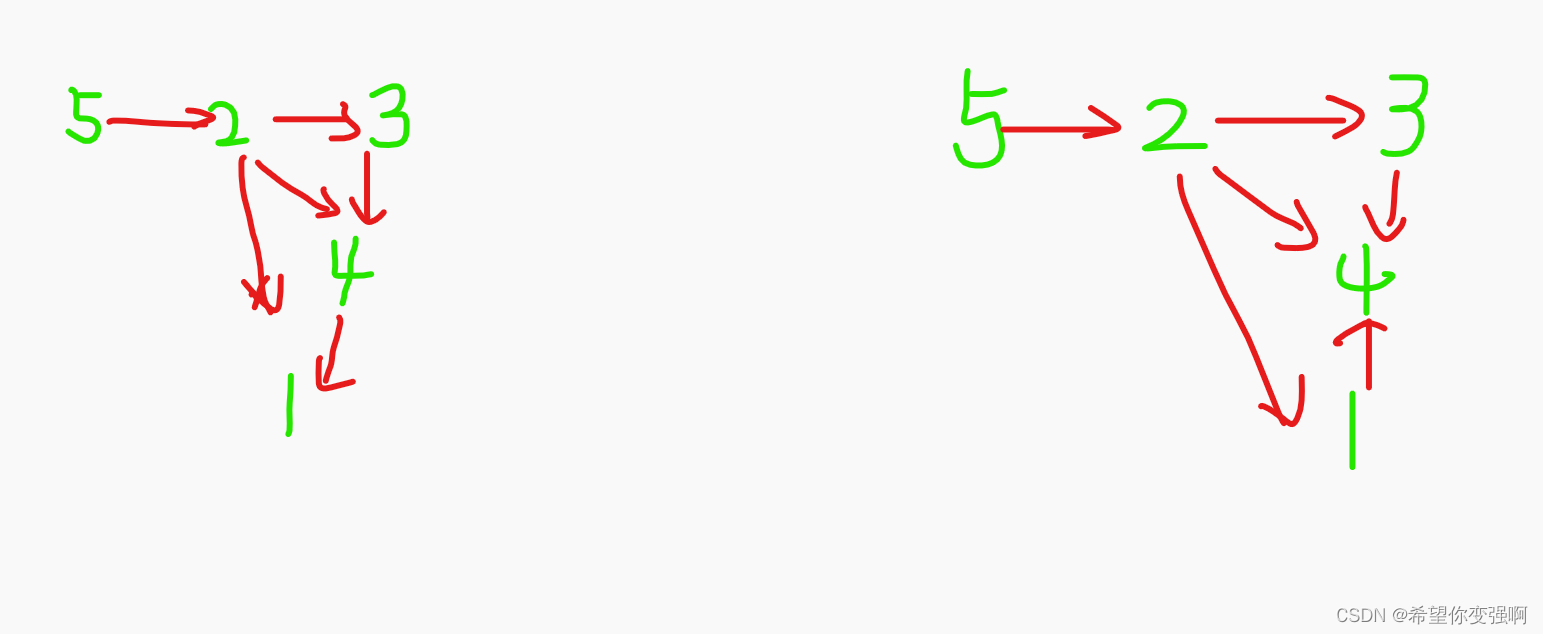
左边是样例一：你会发现5点能到其余点，那么它和其余点的关系就确定了，2能到3,4,1而5能到2，那么2和其余点的关系也确定了……

右边是样例而：你发现5点2点都可以确定，对于3点，它无法到1而1也无法到3，那么3点是不确定的。懂了吗？ 

那么剩下的就是对floyd进行一下小修改：

设置f[i][j]表示<i,j>可以到达(i->j或j->i都行)  那么有

f[i][j]=f[i][j]||f[i][k]&&f[k][j]（||表示只要有一个联通方式即可）

#include <bits/stdc++.h>
using namespace std;
int f[200][200];
int n,m,ans=0;
int main()
{
    cin>>n>>m;int x,y;
    for(int i=1;i<=m;++i){
		cin>>x>>y;f[x][y]=1;
    }
    for(int k=1;k<=n;++k)
      for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j)
        f[i][j]=f[i][j] || (f[i][k] && f[k][j]);
    for(int i=1;i<=n;++i){
        int a=1;
        for(int j=1;j<=n;++j){
            if(i==j) continue;//一定要忽略对角线
            else a=a && (f[i][j] || f[j][i]);//千万不要忘了还有f[j][i]
        }
        ans+=a;
    }
    printf("%d\n",ans);
    return 0;
}