目录
- 1.引言
- 2.混沌映射
- 3.分布特征
- 4.混沌映射函数调用
- 5.改进智能算法
1.引言
基本种群初始化是在整个空间内随机分布,具有较高的随机性和分布不均匀性,会导致种群多样性缺乏,搜索效率低等问题。 许多学者利用混沌映射机制来增加种群的多样性,以改善算法的性能,其非线性特性和周期性质使得它能够生成更复杂、更随机的序列,有助于增加种群的多样性,避免种群陷入局部最优解。
2.混沌映射
Logistic映射
x k + 1 = a x i ( 1 − k i ) (1) x_{k+1}=ax_i(1-k_i)\tag{1} xk+1=axi(1−ki)(1)
Circle映射
x k + 1 = mod ( x k + b − ( a 2 π ) sin ( 2 π x k ) , 1 ) (2) x_{k+1}=\text{mod}\Bigg(x_k+b-\Bigg(\frac{a}{2\pi}\Bigg)\text{sin}\big(2\pi x_k\big),1\Bigg)\tag{2} xk+1=mod(xk+b−(2πa)sin(2πxk),1)(2)
Chebyshev映射
x k + 1 = cos ( a ∗ cos − 1 ( x k ) ) (3) x_{k+1}=\cos(a*\cos^{-1}(x_k))\tag{3} xk+1=cos(a∗cos−1(xk))(3)
Gauss/mouse映射
x k + 1 = { 0 x k = 0 1 m o d ( x k , 1 ) otherwise (4) x_{k+1}=\begin{cases}\quad0&x_k=0\\\dfrac{1}{\mathrm{mod}(x_k,1)}&\text{otherwise}\end{cases}\tag{4} xk+1=⎩ ⎨ ⎧0mod(xk,1)1xk=0otherwise(4)
Piecewise映射
x k + 1 = { x k P 0 ≤ x k < P x k − P 0.5 − P P ≤ x k < 0.5 1 − P − x k 0.5 − P 0.5 ≤ x k < 1 − P 1 − x k P 1 − P ≤ x k < 1 (5) \left.x_{k+1}=\left\{\begin{array}{cc}\frac{x_k}{P}&0\leq x_k<P\\\frac{x_k-P}{0.5-P}&P\leq x_k<0.5\\\frac{1-P-x_k}{0.5-P}&0.5\leq x_k<1-P\\\frac{1-x_k}{P}&1-P\leq x_k<1\end{array}\right.\right.\tag{5} xk+1=⎩ ⎨ ⎧Pxk0.5−Pxk−P0.5−P1−P−xkP1−xk0≤xk<PP≤xk<0.50.5≤xk<1−P1−P≤xk<1(5)
Sine映射
x k + 1 = a 4 sin ( π x k ) (6) x_{k+1}=\frac a4\sin(\pi x_k)\tag{6} xk+1=4asin(πxk)(6)
Singer映射
x k + 1 = a ( 7.86 x k − 23.31 x k 2 + 28.75 x k 3 − 13.302875 x k 4 ) (7) x_{k+1}=a\left(7.86x_k-23.31x_k^2+28.75x_k^3-13.302875x_k^4\right)\tag{7} xk+1=a(7.86xk−23.31xk2+28.75xk3−13.302875xk4)(7)
Iterative映射
x k + 1 = sin ( a π x k ) (8) x_{k+1}=\sin\left(\frac{a\pi}{x_k}\right)\tag{8} xk+1=sin(xkaπ)(8)
Sinusoidal映射
x k + 1 = a x k 2 sin ( π x k ) (9) x_{k+1}=ax_k^2\sin(\pi x_k)\tag{9} xk+1=axk2sin(πxk)(9)
Tent映射
x k + 1 = { x k a x k < a 1 − x k 1 − a x k ≥ a (10) x_{k+1}=\begin{cases}\displaystyle\frac{x_k}{a}&x_k<a\\\ \frac{1-x_k}{1-a}&x_k\geq a\end{cases}\tag{10} xk+1={axk 1−a1−xkxk<axk≥a(10)
Fuch映射
x k + 1 = c o s ( 1 x k 2 ) (11) x_{k+1}=cos\left(\frac{1}{x_k^2}\right)\tag{11} xk+1=cos(xk21)(11)
SPM映射
x k + 1 = { m o d ( x k η + μ sin ( π x k ) + r , 1 ) , 0 ≤ x k < η m o d ( x k / η 0.5 − η + μ sin ( π x k ) + r , 1 ) , η ≤ x k < 0.5 m o d ( ( 1 − x k ) / η 0.5 − η + μ sin ( π ( 1 − x k ) ) + r , 1 ) , 0.5 ≤ x k < 1 − η m o d ( ( 1 − x k ) η + μ sin ( π ( 1 − x k ) ) + r , 1 ) , 1 − η ≤ x k < 1 (12) \left.x_{k+1}=\left\{\begin{array}{c}\mathrm{mod}\left(\frac{x_k}{\eta}+\mu\sin(\pi x_k)+r,1\right),0\leq x_k<\eta\\\\\mathrm{mod}\left(\frac{x_k/\eta}{0.5-\eta}+\mu\sin(\pi x_k)+r,1\right),\eta\leq x_k<0.5\\\\\mathrm{mod}\left(\frac{(1-x_k)/\eta}{0.5-\eta}+\mu\sin(\pi(1-x_k))+r,1\right),0.5\leq x_k<1-\eta\\\\\mathrm{mod}\left(\frac{(1-x_k)}{\eta}+\mu\sin(\pi(1-x_k))+r,1\right),1-\eta\leq x_k<1\end{array}\right.\right.\tag{12} xk+1=⎩ ⎨ ⎧mod(ηxk+μsin(πxk)+r,1),0≤xk<ηmod(0.5−ηxk/η+μsin(πxk)+r,1),η≤xk<0.5mod(0.5−η(1−xk)/η+μsin(π(1−xk))+r,1),0.5≤xk<1−ηmod(η(1−xk)+μsin(π(1−xk))+r,1),1−η≤xk<1(12)
ICMIC映射
x k + 1 = sin ( a x k ) (13) x_{k+1}=\sin\left(\frac{a}{x_k}\right)\tag{13} xk+1=sin(xka)(13)
Kent映射
x k + 1 = { − x k / a , 0 < x k ⩽ a ( 1 − x k ) / ( 1 − a ) , a < x k < 1 (14) x_{k+1}=\begin{cases}\phantom{-}x_k/a,&0<x_k\leqslant a\\\left(1-x_k\right)/(1-a),&a<x_k<1\end{cases} \tag{14} xk+1={−xk/a,(1−xk)/(1−a),0<xk⩽aa<xk<1(14)
Cubic映射
x k + 1 = a x k ( 1 − x k 2 ) (15) x_{k+1}=ax_k\left(1-{x_k}^2\right)\tag{15} xk+1=axk(1−xk2)(15)
Bernoulli映射
x k + 1 = { x k / ( 1 − a ) , x k ∈ ( 0 , 1 − a ] ( x k − 1 + a ) / a , x k ∈ ( 1 − a , 1 ) (16) x_{k+1}=\begin{cases}x_k/(1-a),&x_k\in(0,1-a]\\\left(x_k-1+a\right)/a,&x_k\in(1-a,1)\end{cases}\tag{16} xk+1={xk/(1−a),(xk−1+a)/a,xk∈(0,1−a]xk∈(1−a,1)(16)
Logistic-Tent映射
x k + 1 = { ( r x k ( 1 − x k ) + ( 4 − r ) x k / 2 ) m o d 1 , x k < 0.5 ( r x k ( 1 − x k ) + ( 4 − r ) ( 1 − x k ) / 2 ) m o d 1 , x k ⩾ 0.5 (17) x_{k+1}=\begin{cases}\left(rx_{k}\left(1-x_{k}\right)+(4-r)x_k/2\right){\mathrm{mod}}1,x_{k}<0.5 \\\left(rx_k\left(1-x_k\right)+\left(4-r\right)\left(1-x_k\right)/2\right){\mathrm{mod}}1,x_k\geqslant0.5\end{cases}\tag{17} xk+1={(rxk(1−xk)+(4−r)xk/2)mod1,xk<0.5(rxk(1−xk)+(4−r)(1−xk)/2)mod1,xk⩾0.5(17)
Logistic-Tent-Cosine映射
x k + 1 = { cos ( π ( 2 r x k + 4 ( 1 − r ) x k ( 1 − x k ) − 0.5 ) ) , if x k < 0.5 cos ( π ( 2 r ( 1 − x k ) + 4 ( 1 − r ) x k ( 1 − x k ) − 0.5 ) ) , else (18) x_{k+1}=\begin{cases}\cos(\pi(2rx_k+4(1-r)x_k(1-x_k)-0.5)),\text{ if }x_k<0.5\\\cos(\pi(2r(1-x_k)+4(1-r)x_k(1-x_k)-0.5)),\text{ else }\end{cases}\tag{18} xk+1={cos(π(2rxk+4(1−r)xk(1−xk)−0.5)), if xk<0.5cos(π(2r(1−xk)+4(1−r)xk(1−xk)−0.5)), else (18)
Sine-Tent-Cosine映射
x k + 1 = { cos ( π ( r sin ( π x k ) + 2 ( 1 − r ) x k − 0.5 ) ) , if x k < 0.5 cos ( π ( r sin ( π x k ) + 2 ( 1 − r ) ( 1 − x k ) − 0.5 ) ) , else (19) x_{k+1}=\begin{cases}\cos(\pi(r\sin(\pi x_k)+2(1-r)x_k-0.5)),\text{if} x_k<0.5\\\cos(\pi(r\sin(\pi x_k)+2(1-r)(1-x_k)-0.5)),\text{else}\end{cases}\tag{19} xk+1={cos(π(rsin(πxk)+2(1−r)xk−0.5)),ifxk<0.5cos(π(rsin(πxk)+2(1−r)(1−xk)−0.5)),else(19)
Logistic-Sine-Cosine映射
x k + 1 = cos ( π ( 4 r x k ( 1 − x k ) + ( 1 − r ) sin ( π x k ) − 0.5 ) ) (20) x_{k+1}=\cos\Big(\pi\Big(4rx_k\big(1-x_k\big)+(1-r)\sin\big(\pi x_k\big)-0.5\big)\Big)\tag{20} xk+1=cos(π(4rxk(1−xk)+(1−r)sin(πxk)−0.5))(20)
3.分布特征
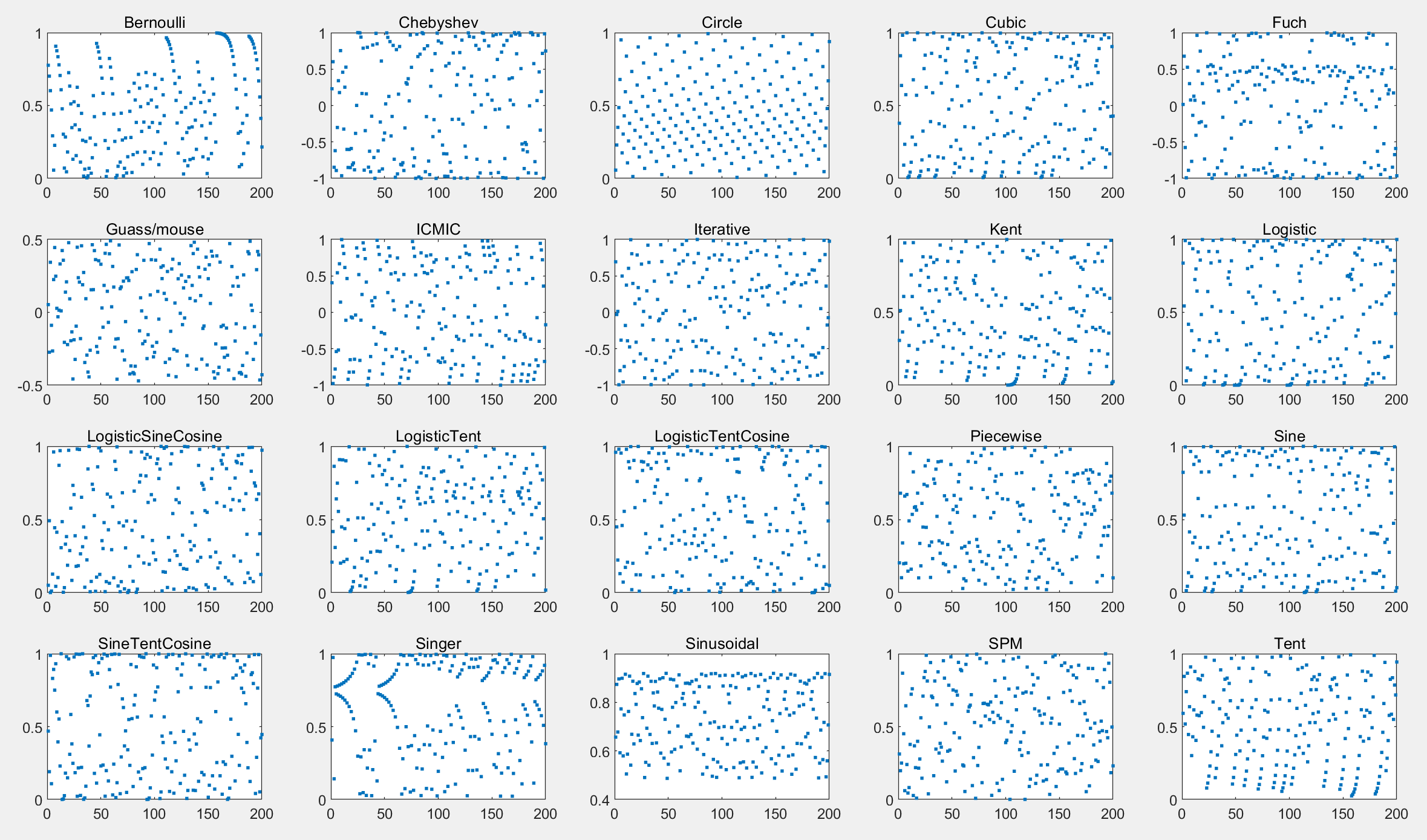

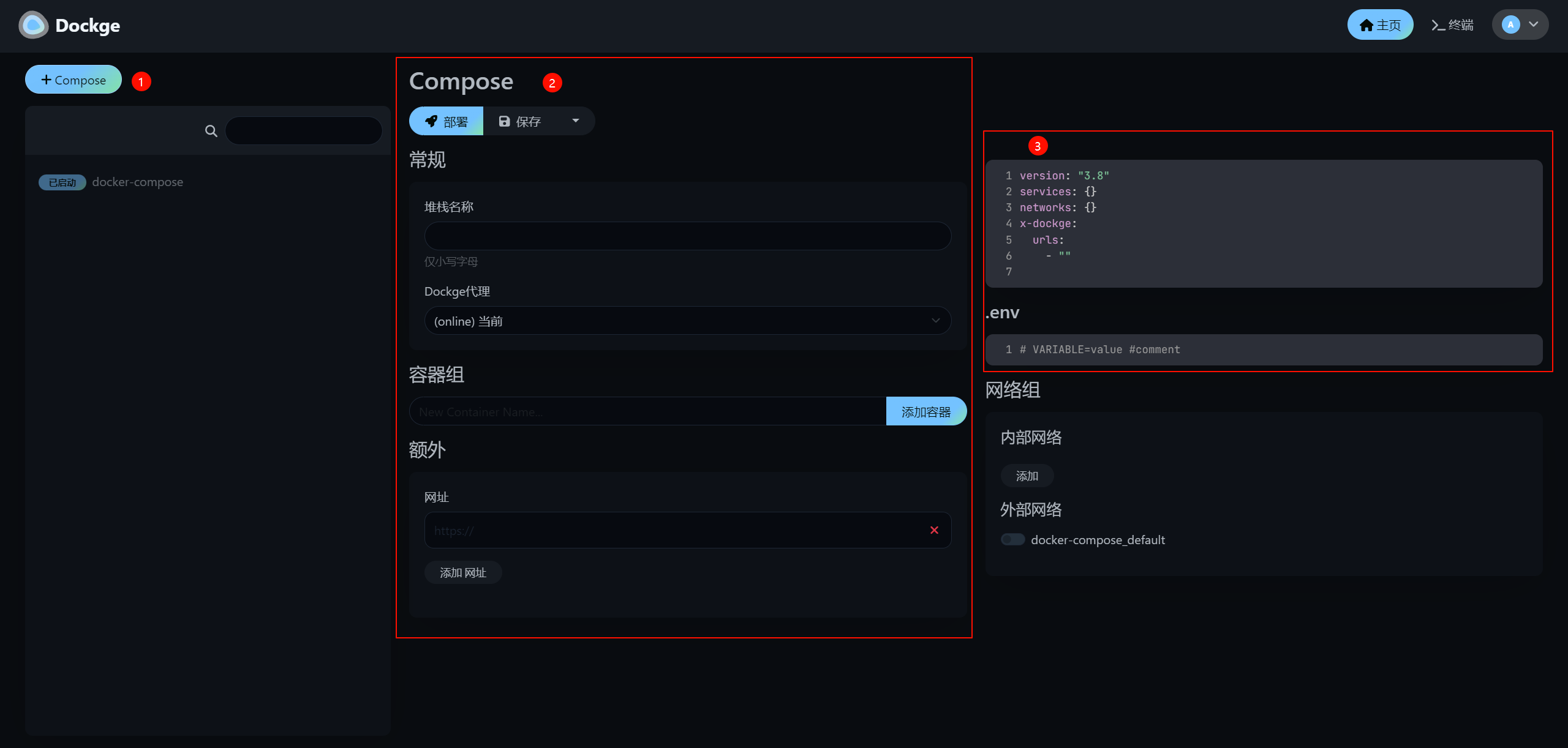
4.混沌映射函数调用

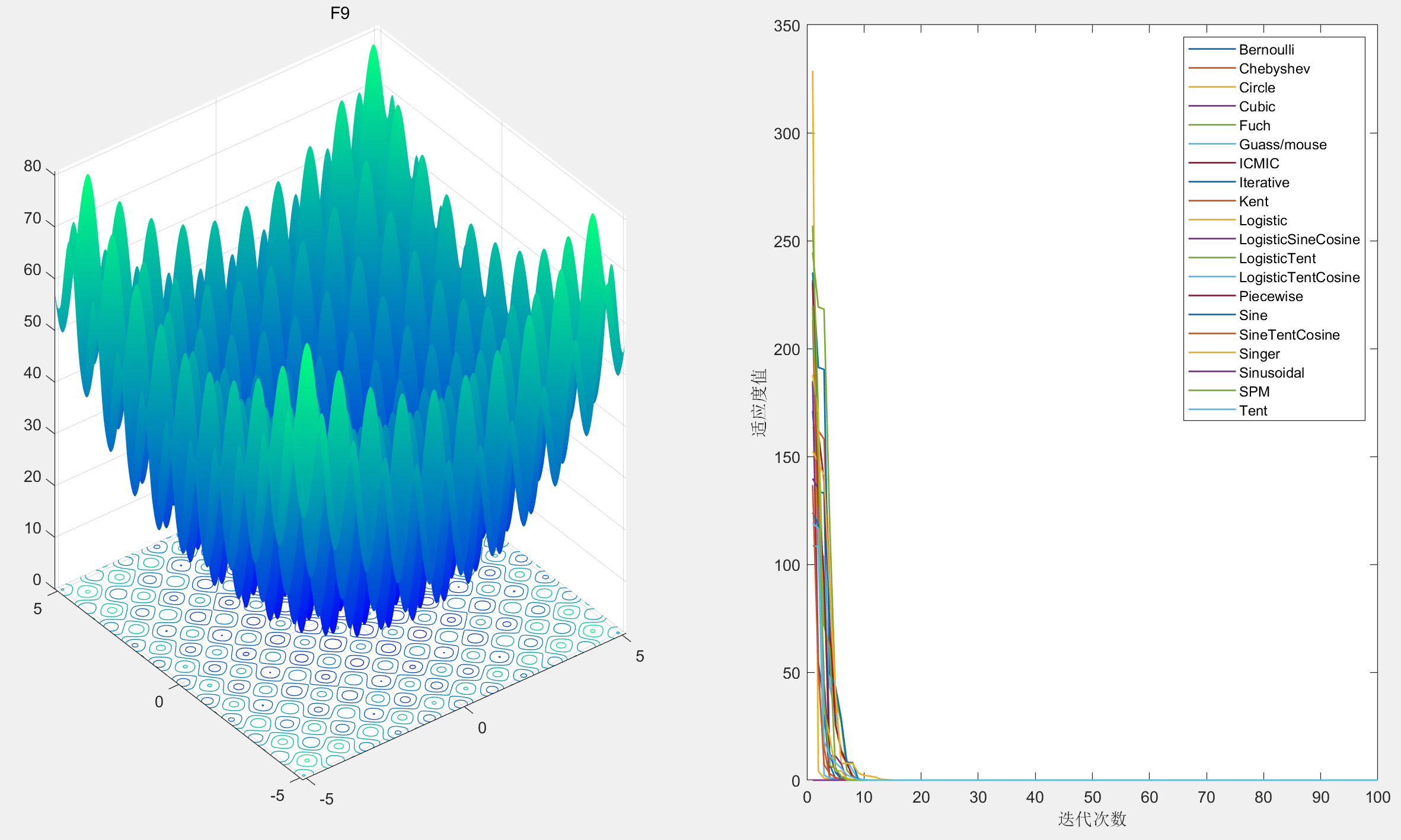
5.改进智能算法
混沌映射用于初始化哈里斯鹰算法(HHO),结果如下: