螺旋矩阵的算法刷题
本文主要涉及螺旋矩阵的算法
包括三个题目分别是
- 59. 螺旋矩阵 II
- 54. 螺旋矩阵 中等
- LCR 146. 螺旋遍历二维数组
文章目录
- 螺旋矩阵的算法刷题
- 一 、螺旋矩阵简单
- 1.1 实现一(我认为这个方法更巧妙!!)
- 1.2 实现二(经典方法--更加直观)
- 二、螺旋矩阵 中等
- 2.1 实现一(经典)
- 2.2 实现二(精妙!!)
- 三、螺旋遍历矩阵 简单
一 、螺旋矩阵简单
59. 螺旋矩阵 II
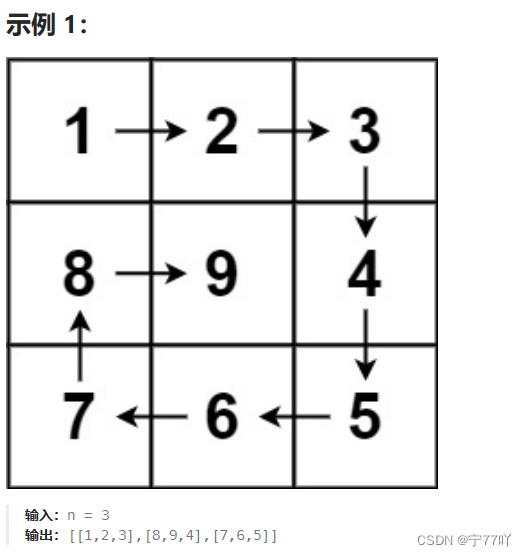
给你一个正整数 n ,生成一个包含 1 到 n2 所有元素,且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix .
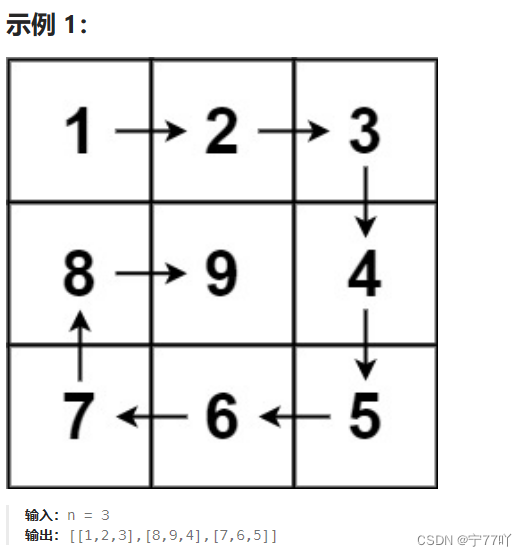
1.1 实现一(我认为这个方法更巧妙!!)
思路:
采用了类似螺旋走位的方式进行填充,具体实现如下:
- 首先,定义一个n x n的二维数组res来存储结果。
- 初始化方向向量dx和dy,初始值分别为0和1,表示向右移动。
- 初始化坐标x和y,初始值都为0,表示从矩阵的左上角开始填充。
- 使用一个循环,从1到n * n遍历每个要填充的数字。
- 在每一步中,将当前位置的值设置为当前遍历的数字i,并根据当前方向向量(dx, dy)进行移动到下一个位置。
- 判断下一个位置是否已经被填充过,如果是,则表示已经到达边界,需要调转方向向量以继续填充;如果不是,则继续沿当前方向向量移动。
- 返回填充完成的二维数组res作为结果。
这样的算法可以确保填充的数字形成了一个螺旋状的矩阵。
C++代码实现
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> matrix(n,vector<int>(n,0));
//代表方向的向量变量 01--右 10--下 -1 0--左 0 -1 --上
int dx=0,dy=1;
//x,y表示当前坐标
int x=0,y=0;
//使用for进行循环,i表示当前值
for(int i =1; i<=n*n;i++)
{
matrix[x][y]=i;
//**关键部分**
if(matrix[(x+dx+n)%n][(y+dy+n)%n]!=0)//判断是否已经填充,如果已经填充则向量需要换方向
{
int temp = dy;
dy=-dx;
dx=temp;
}
x+=dx;
y+=dy;
}
return matrix;
}
};
重要的是下面这段代码
if(matrix[(x+dx+n)%n][(y+dy+n)%n]!=0)//判断是否已经填充,如果已经填充则向量需要换方向
{
int temp = dy;
dy=-dx;
dx=temp;
}
这段代码是在判断当前位置的下一个位置是否已经被填充过。如果下一个位置已经被填充过,说明当前位置已经是当前层的最后一个位置,需要改变填充方向。
逐行解释这段代码:
(x + dx + n) % n:这里计算了下一个位置的横坐标。由于是螺旋填充,因此下一个位置可能超出边界。使用% n可以将超出边界的情况转化为在边界内的情况。例如,当x + dx大于等于n时,超出了右边界,通过% n可以将其映射到左边界,从而形成循环填充。- 同理,
(y + dy + n) % n计算了下一个位置的纵坐标。 res[(x + dx + n) % n][(y + dy + n) % n] != 0:这个条件判断当前位置的下一个位置是否已经被填充过。如果下一个位置不等于0,说明已经被填充过。- 如果下一个位置已经被填充过,则需要改变填充方向。通过交换
dx和dy实现了向下转向的功能。 int tem = dy; dy = -dx; dx = tem;:这里使用了一个临时变量tem,先将dy的值保存下来,然后将dy设置为-dx,dx设置为tem,实现了方向的转换。
总的来说,这段代码的作用是在当前位置的下一个位置已经被填充过时,改变填充方向,从而继续填充螺旋矩阵。
1.2 实现二(经典方法–更加直观)
一个常见的方法是按层次遍历,逐层填充螺旋矩阵。具体步骤如下:
- 初始化一个n x n的二维数组res,用于存储结果。
- 定义四个变量top、bottom、left、right,分别表示当前填充层的上下左右边界。
- 初始化这些边界值:top=0,bottom=n-1,left=0,right=n-1。
- 初始化一个变量num,表示当前要填充的数字,初始值为1。
- 在一个循环中,依次填充每一层的数字,直到所有位置都被填充为止。
- 从左到右,将当前层的最上一行从left到right填充为num开始递增的数字,同时更新top的值使其向下移动一行。
- 从上到下,将当前层的最右一列从top到bottom填充为num开始递增的数字,同时更新right的值使其向左移动一列。
- 从右到左,将当前层的最下一行从right到left填充为num开始递增的数字,同时更新bottom的值使其向上移动一行。
- 从下到上,将当前层的最左一列从bottom到top填充为num开始递增的数字,同时更新left的值使其向右移动一列。
- 每填充完一行或一列后,将num递增。
- 当top > bottom 或 left > right时,表示所有位置都被填充完毕,退出循环。
- 返回填充完成的二维数组res作为结果。
这样的实现方法更直观清晰,容易理解和实现,并且效率也很高。
class Solution {
public:
vector<vector<int>> generateMatrix(int n) {
vector<vector<int>> res(n, vector<int>(n, 0)); // 初始化结果矩阵为全零
int top = 0, bottom = n - 1, left = 0, right = n - 1; // 初始化边界
int num = 1; // 当前要填充的数字,初始为1
while (true) {
// 从左到右,填充最上一行
for (int i = left; i <= right; ++i) {
res[top][i] = num++;
}
if (++top > bottom) break; // 更新上边界,若超过下边界则退出
// 从上到下,填充最右一列
for (int i = top; i <= bottom; ++i) {
res[i][right] = num++;
}
if (--right < left) break; // 更新右边界,若超过左边界则退出
// 从右到左,填充最下一行
for (int i = right; i >= left; --i) {
res[bottom][i] = num++;
}
if (--bottom < top) break; // 更新下边界,若超过上边界则退出
// 从下到上,填充最左一列
for (int i = bottom; i >= top; --i) {
res[i][left] = num++;
}
if (++left > right) break; // 更新左边界,若超过右边界则退出
}
return res;
}
};
二、螺旋矩阵 中等
54. 螺旋矩阵 中等
给你一个 m 行 n 列的矩阵 matrix ,请按照 顺时针螺旋顺序 ,返回矩阵中的所有元素。
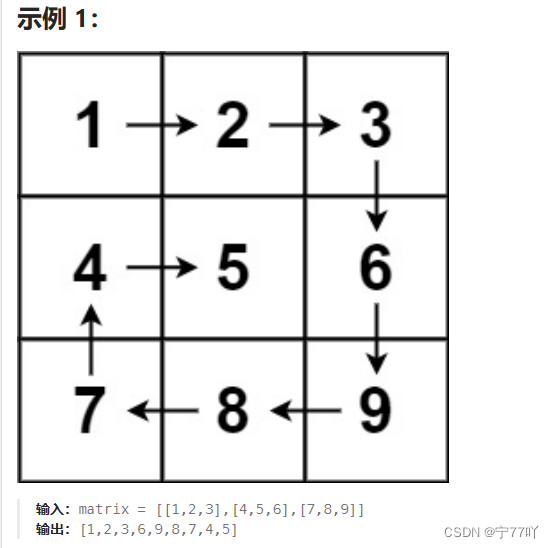
2.1 实现一(经典)
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> ans;
if (matrix.empty()) return ans;
int m = matrix.size(); // 行数
int n = matrix[0].size(); // 列数
int top = 0, bottom = m - 1, left = 0, right = n - 1;
while (top <= bottom && left <= right) {
// 从左到右遍历上边界
for (int j = left; j <= right; ++j) {
ans.push_back(matrix[top][j]);
}
++top;
// 从上到下遍历右边界
for (int i = top; i <= bottom; ++i) {
ans.push_back(matrix[i][right]);
}
--right;
// 从右到左遍历下边界
if (top <= bottom) { // 防止重复访问上一次遍历的元素
for (int j = right; j >= left; --j) {
ans.push_back(matrix[bottom][j]);
}
--bottom;
}
// 从下到上遍历左边界
if (left <= right) { // 防止重复访问上一次遍历的元素
for (int i = bottom; i >= top; --i) {
ans.push_back(matrix[i][left]);
}
++left;
}
}
return ans;
}
};
按照螺旋顺序遍历二维矩阵。下面是对代码的详细解释:
- 首先,定义一个空的整数向量
ans用于存储遍历结果。 - 如果输入的二维矩阵
matrix为空,直接返回空的结果向量ans。 - 获取矩阵的行数
m和列数n,以及初始化四个边界变量top、bottom、left和right。 - 在一个循环中,不断遍历矩阵的边界元素,直到边界收缩到无效为止。
- 从左到右遍历上边界,将上边界的元素依次加入结果向量
ans中,并将top上移一行。 - 从上到下遍历右边界,将右边界的元素依次加入结果向量
ans中,并将right右移一列。 - 从右到左遍历下边界,将下边界的元素依次加入结果向量
ans中,并将bottom下移一行(注意要判断top <= bottom,防止重复遍历)。 - 从下到上遍历左边界,将左边界的元素依次加入结果向量
ans中,并将left左移一列(注意要判断left <= right,防止重复遍历)。
- 从左到右遍历上边界,将上边界的元素依次加入结果向量
- 循环结束后,返回结果向量
ans。
利用边界变量控制了螺旋顺序的遍历过程,实现了按照螺旋顺序遍历二维矩阵的功能。
2.2 实现二(精妙!!)
下面是一段Python代码:
def spiralOrder(self, matrix: List[List[int]]) -> List[int]:
res = []
while matrix:
# 削头(第一层)
res += matrix.pop(0)
# 将剩下的逆时针转九十度,等待下次被削
matrix = list(zip(*matrix))[::-1]
return res
采用了不断“削头”的方式来实现。具体的步骤如下:
- 创建一个空列表
res用于存储螺旋顺序遍历的结果。 - 使用
while matrix:循环来遍历矩阵,直到矩阵为空。 - 在每一次循环中,先将矩阵的第一行(即第一层)添加到结果列表
res中,然后将该行从矩阵中移除。 - 接着,将剩下的矩阵逆时针旋转 90 度(将其转置后再沿着竖直方向反转),以便下次循环时能够继续削头。
- 重复上述步骤直到矩阵为空。
这种方法的思路简洁,通过不断调整矩阵的结构来实现螺旋顺序遍历,避免了显式的控制遍历方向和边界条件的处理。
在实际代码中,matrix.pop(0) 用于削头,list(zip(*matrix))[::-1] 用于逆时针旋转矩阵。
如果是C++实现类似削头的效果:
#include <vector>
class Solution {
public:
vector<int> spiralOrder(vector<vector<int>>& matrix) {
vector<int> res;
while (!matrix.empty()) {
// 削头(第一层)
for (auto it = matrix[0].begin(); it != matrix[0].end(); ++it) {
res.push_back(*it);
}
matrix.erase(matrix.begin()); // 删除第一行
// 将剩下的逆时针转九十度,等待下次被削
if (!matrix.empty()) {
vector<vector<int>> new_matrix;
for (int j = matrix[0].size() - 1; j >= 0; --j) {
vector<int> column;
for (int i = 0; i < matrix.size(); ++i) {
column.push_back(matrix[i][j]);
}
new_matrix.push_back(column);
}
matrix = new_matrix;
}
}
return res;
}
};
三、螺旋遍历矩阵 简单
LCR 146. 螺旋遍历二维数组
上面这个题是企业题,同类型的题目可以多练习练习~