本文主要参考Probabilistic Robotics《概率机器人》一书。
其他参考：
弗莱堡大学课件
博客
含代码博客

0.引言

位姿已知的地图构建(mapping with known poses)的定义：已知机器人的位姿$x_{1:t}$和传感器的观测数据$z_{1:t}$求解最可能的地图$m^{\ast }=\arg {\max }_{m}P(m|x_{1:t},z_{1:t})$
占用栅格地图，顾名思义地图形式是栅格形式，即将环境分为小格子
$m_i$表示第i个栅格单元，占用栅格地图将空间分割为有限多个栅格地图 m = { m i } m=\{m_i\} m={mi​}，每个$m_i$与一个二值占用变量相对应，该变量指示出该单元是否被占用，被占用设为1，未被占用设为0。$p(m_i)$表示该栅格单元被占用的可能性。
为所有的栅格建立后验概率$p(m_i|z_{1:t},x_{1:t})$，那么构建地图公式变为
$$\begin{gathered} P(m|x_{1:t},z_{1:t})=p(m_1,m_2,...,m_n|x_{1:t},z_{1:t}) \\ =\sum _{i=1}^{n}p(m_i|z_{1:t},x_{1:t})（假设每个格子独立同分布） \end{gathered}$$

但是这种独立同分布抛弃了相邻单元之间的联系，并不是最优解，对于这一点，我们暂且不讨论。

1. 静态二值贝叶斯滤波

上面这个独立同分布的地图构建公式可以看作一个静态二值贝叶斯滤波(binary Bayes filter)——不随时间变化的二值状态的最优估计问题。
对于一个格子被占有的概率记为——置信度$bel(m_i)=p(m_i|x_{1:t},z_{1:t})$，最终通过设置阈值来确定哪些格子是占有栅格(例如$bel(m_i)>0.6$)，哪些是空闲栅格(例如$bel(m_i)<0.4$)，哪些是未知栅格($0.4\le bel(m_i)\le 0.6$)。
求解占有栅格的置信度：
$$be{l}_t(m_i)=p(m_i|z_{1:t},x_{1:t})$$

同理可得出空闲栅格的置信度
利用两式相除消去部分未知部分：
二值Bayes滤波递归更新公式$l_{t,i}=l_{t-1,i}+l_{inv,i}-l_0$，更新后在求置信度：
$$be{l}_t{m}_i=1-\frac{1}{1+\exp (l_{t,i})}$$
初始时刻栅格的占用情况未知，将其置信度设为$be{l}_0(m_i)=0.5$,则先验概率$l_0=0$

2.反演测量模型

2.1 声纳模型

来自PR一书和弗莱堡大学ppt中的模型，当某一个测量点距离为z，分别设置了z-d1,z+d1,z+d2,z+d3的占据概率。其中0-(z-d1)为free，(z-d1)-(z+d3)为occ，(z+d3)之后为no info。

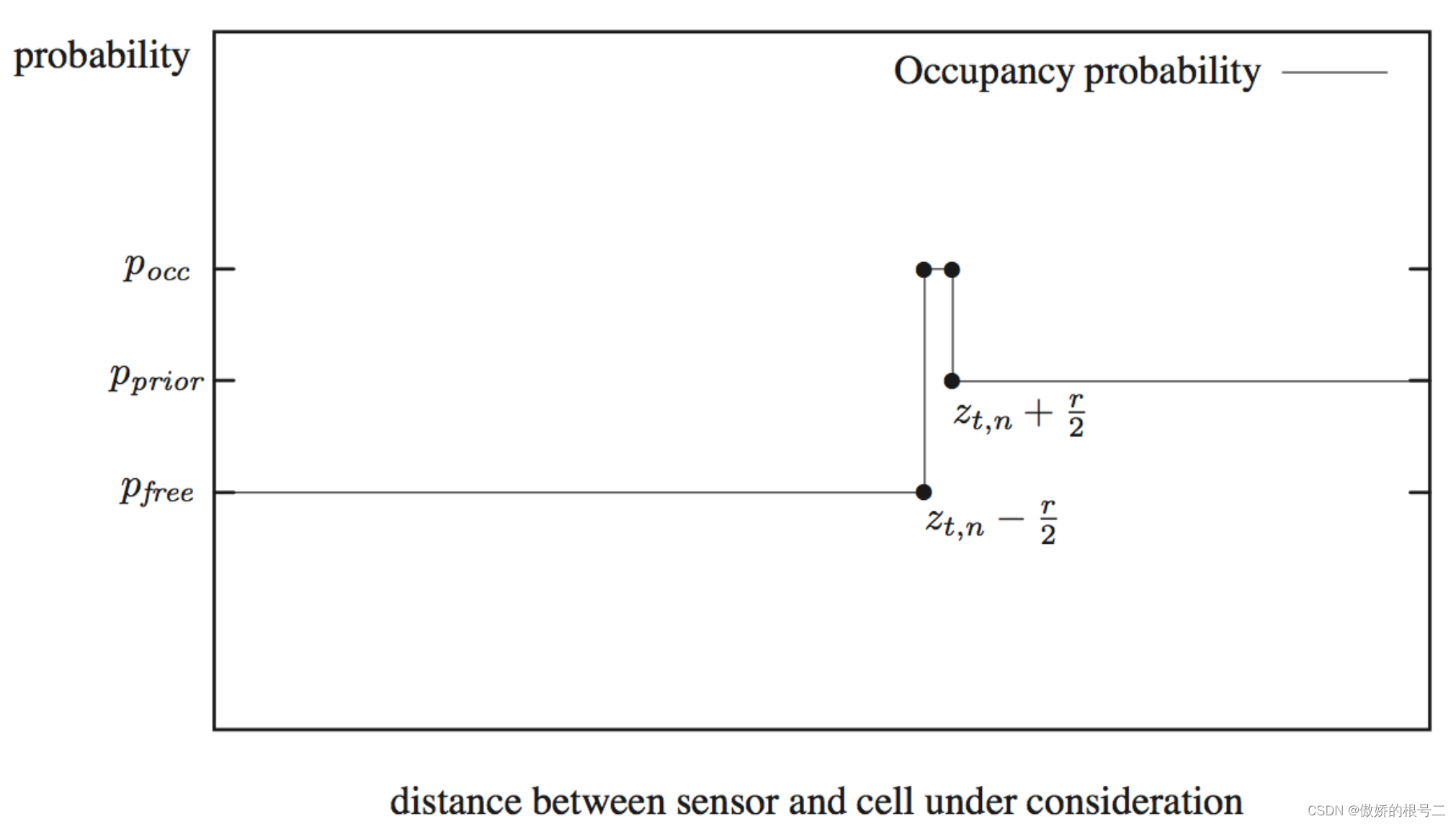
2.2激光传感器模型

#include <occ_grid_mapping/grid_mapper.h>

GridMapper::GridMapper ( GridMap* map, Pose2d& T_r_l, double& P_occ, double& P_free, double& P_prior):
map_(map), T_r_l_(T_r_l), P_occ_(P_occ), P_free_(P_free), P_prior_(P_prior){}

void GridMapper::updateMap ( const sensor_msgs::LaserScanConstPtr& scan,  Pose2d& robot_pose )
{
    /* 获取激光的信息 */
    const double& ang_min = scan->angle_min;        //雷达起始角度
    const double& ang_max = scan->angle_max;        //雷达终止角度
    const double& ang_inc = scan->angle_increment;  //角度增量(角度分辨率)
    const double& range_max = scan->range_max;      //雷达数据的最小值
    const double& range_min = scan->range_min;      //雷达数据的最大值
    
    /* 设置遍历的步长，沿着一条激光线遍历 */
    const double& cell_size = map_->getCellSize();
    const double inc_step = 1.0 * cell_size;

    /* for every laser beam */
    for(size_t i = 0; i < scan->ranges.size(); i ++)
    {
        /* 获取当前beam的距离 */
        double R = scan->ranges.at(i); 
        if(R > range_max || R < range_min)
            continue;
        
        /* 沿着激光射线以inc_step步进，更新地图*/
        double angle = ang_inc * i + ang_min;
        double cangle = cos(angle);
        double sangle = sin(angle);
        Eigen::Vector2d last_grid(Eigen::Infinity, Eigen::Infinity); //上一步更新的grid位置，防止重复更新
        for(double r = 0; r < R + cell_size; r += inc_step)
        {
            Eigen::Vector2d p_l(
                r * cangle,
                r * sangle
            ); //在激光雷达坐标系下的坐标
            
            /* 转换到世界坐标系下 */
            Pose2d laser_pose = robot_pose * T_r_l_;
            Eigen::Vector2d p_w = laser_pose * p_l;

            /* 更新这个grid */
            if(p_w == last_grid) //避免重复更新
                continue;
            
            updateGrid(p_w, laserInvModel(r, R, cell_size));    //更新占据概率
            	    
            last_grid = p_w;
        }//for each step
    }// for each beam
}

void GridMapper::updateGrid ( const Eigen::Vector2d& grid, const double& pmzx )
{
    /* TODO 这个过程写的太低效了 */
    double log_bel;
    if(  ! map_->getGridLogBel( grid(0), grid(1), log_bel )  ) //获取log的bel
        return;
    log_bel += log( pmzx / (1.0 - pmzx) ); //更新
    map_->setGridLogBel( grid(0), grid(1), log_bel  ); //设置回地图
}

//雷达的反演测量模型
double GridMapper::laserInvModel ( const double& r, const double& R, const double& cell_size )
{
    if(r < ( R - 0.5*cell_size) )
        return P_free_;
    
    if(r > ( R + 0.5*cell_size) )
        return P_prior_;
    
    return P_occ_;
}