红黑树的Java实现

---

---

一、概述

• 红黑树也是一种二叉平衡搜索树，向比与AVL树，是一种弱平衡树。因为AVL树是通过平衡因子，左右树的高度相差不能大于1来保证平衡，而红黑树的左右字数的高度差并不固定，可以大于1，也没有平衡因子的概念。它是通过维护五条性质来保证红黑树是平衡的。
• 红黑树五条性质：
  1. 节点是 RED 或者 BLACK。
  2. 根节点是 BLACK。
  3. 叶子结点（外部节点，空节点）都是 BLACK。
  4. RED 节点的子节点都是 BLACK。可类比出两条性质
     • RED 节点的 parent 都是 BLACK。
     • 从根节点到叶子结点的所有路径上不能有2个连续的 RED 节点。
  5. 从任一节点到**叶子结点**的所有路径都包含相同数目的 BLACK 节点。
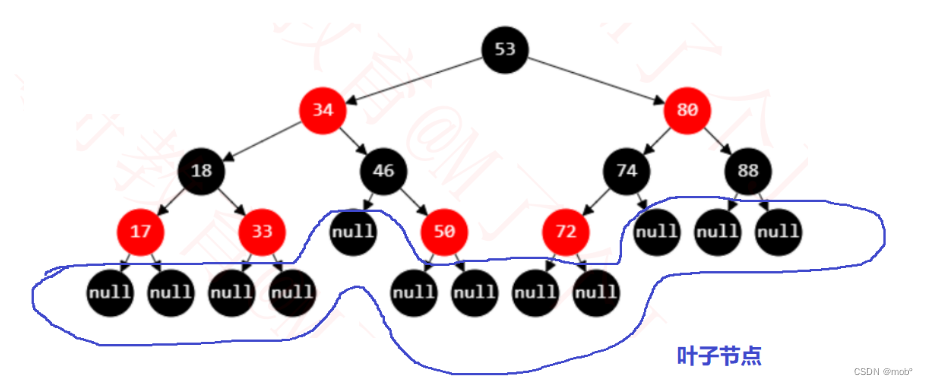
• 注意性质三：红黑树的叶子结点和其他树的叶子节点不一样。红黑树的叶子结点是假象的节点。且都是 BLACK。
  • 红黑树会让原来那些度为0（例如17、33…）、度为1（例如46、74…）的节点都变成度为2的节点。那么怎么变呢？很简单，给它新增null的子节点即可。红黑树所说的叶子节点是指那些null节点，我们也可以将这些null节点称为外部节点，并且这些null节点（外部节点）是我们为了理解（满足）红黑树的一些性质而假想出来的，我们平时写代码的时候不用将这些节点加进去。给红黑树的每个度为0和度为1的节点加上null的子节点后，这颗红黑树就成为了一颗真二叉树（真二叉树：度要么为0要么为2）。观察上图不难得知：红黑树中度为0的节点都是那些假想出来的null节点，原来的那些不为空的那些节点的度都为2。

二、添加元素

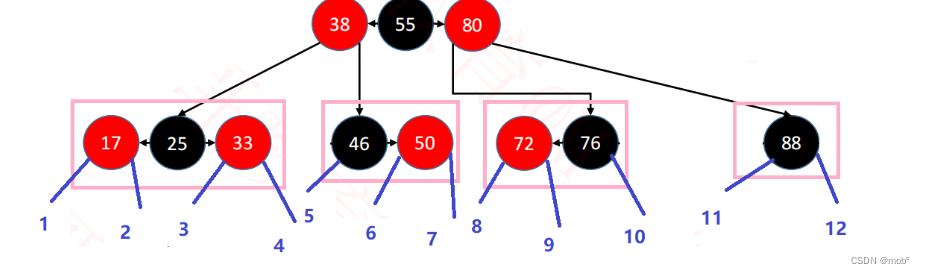
• 红黑树的添加只会将元素 添加到叶子节点中，且只有这十二种情况。同时可分三类讨论。

• 新添加的元素默认为红色，这样可以让红黑树尽快的满足（1，2，3，5都满足，性质4不一定）。
  

  1. 如果新添加节点的父节点为黑色，直接添加，无需做任何处理。
     

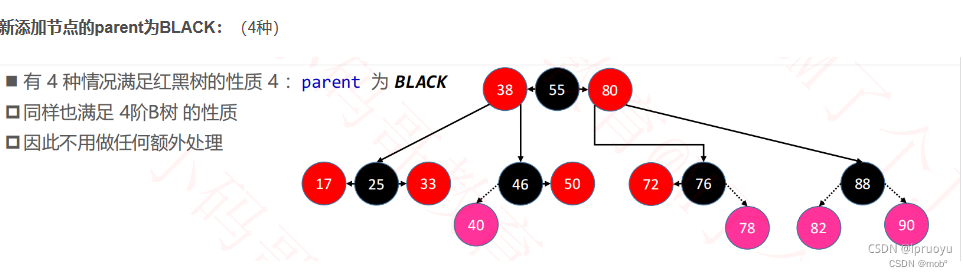
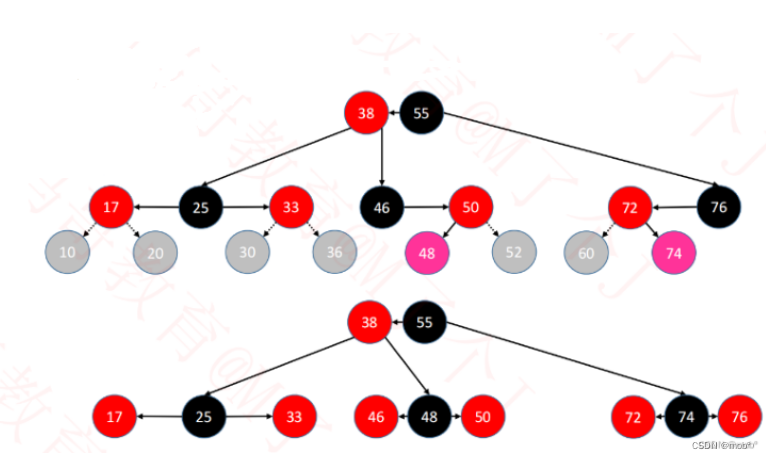
  2. 如果添加节点的父节点为红色，且 uncle 为 黑色。（空节点也认为是黑色，如76的右子节点为黑色）则需要旋转来调整平衡，和 BBST 旋转一样的。
     

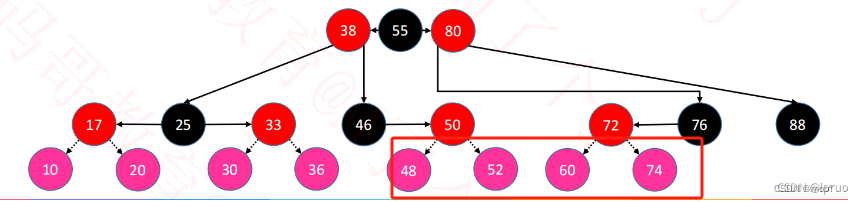
     • 56 和 60 的情况旋转一次即可。
       

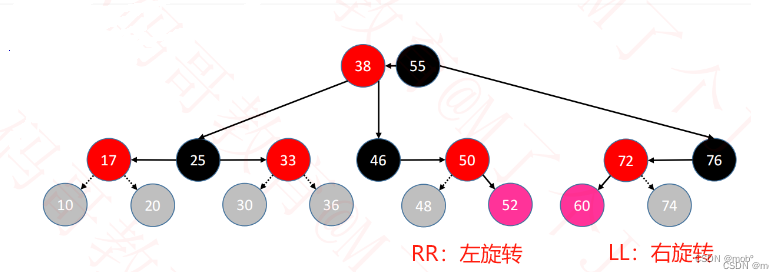
     • 48、74则需要旋转两次。 48 先右旋转再46左旋转。72先左旋转再76右旋转。（旋转的时候注意是将高位的旋转之至低位，低位的旋转至低位，并且是以高位的的为旋转点）
       

  3. 如果添加节点的父节点为红色，且 uncle 为 红色。则需要通过上溢来恢复平衡。注： 这里的上溢是我们类比红黑树为一个4阶B树，通过假想所有的红色节点和父节点进行合并形成 “4解B树的一个节点”，B树的上溢是将关键字拆分合并到父节点的关键字中，是 真实的上溢，而由于红黑树的红色节点和父类节点合并是假象的，所以只需要通过染色来达到上溢的效果即可。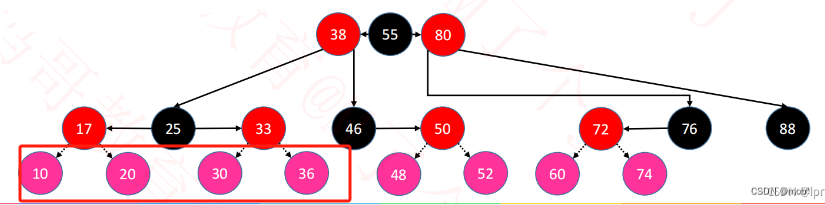

     

• 都是通过将 grand 节点染成红色，达到让 grand 完成上溢的效果，同时需要将parent 和 uncle 节点染成褐色节点即可。由于上溢的gand 节点可能会导致新的不平衡，没关系，将grand 当成新添加的节点到 grand.parend，递归调用分析grand这次 ‘添加’是哪种情况即可。

• 下面是添加元素代码，我也标注了各个代码出所代表的是上面哪种情况。

  public void add(V v){
          //创建新节点且为红色
          RBTreeNode<V> newNode = new RBTreeNode<>(v);
          //如果是第一次插入
          if (root == null){
              root = new RBTreeNode<>(v);;
              //根节点必须染为黑色
              root.black();
              return;
          }
          //不是第一次插入：
          addNode(newNode);
      }
  
  public void addNode(RBTreeNode<V> newNode) {
          //查找应该插入到哪个叶子节点下面
          RBTreeNode<V> parentNode = findParentNode(root, newNode.value);
          int comp = compare(parentNode.value,newNode.value);
          //插入新节点
          newNode.parent = parentNode;
          if (comp > 0){
              parentNode.left = newNode;
          }else {
              parentNode.right = newNode;
          }
          if (isRed(parentNode)){
              //1.如果父节点为黑色，则直接插入
              return;
          }
          //2.如果父节点是 RED，且 uncle 节点是 BLACK
          RBTreeNode<V> grand = parentNode.parent;
          if (grand != null){
              if (!parentNode.uncle()){
                  if (parentNode.isRight()){// right
                      if(comp > 0){ // Left
                          // 右旋
                          rightRotate(parentNode);
                          // 左旋
                          leftRotate(grand);
                      }else { // right
                          // 左旋
                          leftRotate(parentNode);
                      }
                  }else { // Left
                      if(comp > 0){// left
                          // 右旋
                          rightRotate(parentNode);
                      }else { // right
                          // 左旋
                          leftRotate(parentNode);
                          // 右旋
                          rightRotate(grand);
                      }
                  }
                  return;
              }
              //3.如果父节点是 RED，且 uncle 节点是 RED
              //上溢
              upOverFlow(newNode);
          }
      }
  

三、删除元素

• 红黑树删除节点很复杂，分为很多中情况，这里做个总结与归纳。

  1. 如果删除的是 叶子节点且为红色节点，直接删除即可，无需左任何处理。
     
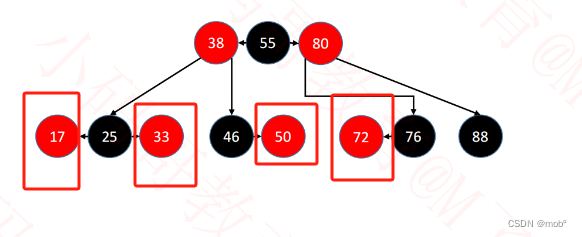
  2. 如果被删除的节点是黑色节点且该黑色节点拥有红色的子节点（无所谓度为1或2），则用红色的字节代替黑色节点，然后直接删除红色节点。注：这里可直接用子节点覆盖需要被删除节点值并删用来覆盖的子节点，也可通过改变指针指向来删除。

  
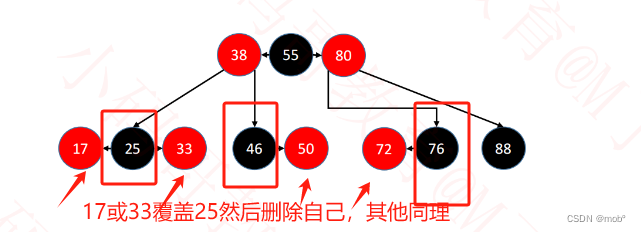
  3. 如果删除的是节点为黑色且兄弟节点也为黑色。需要分情况讨论：这种情况可以类比B树（4阶B树）和 AVL树。

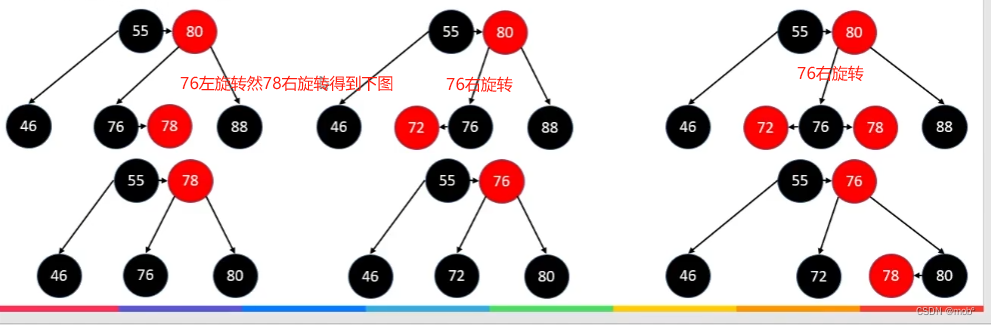
  • 如果兄弟节点是黑色且有至少一个红色子节点。则进行旋转操作，之后将新的父节颜色继承原先的父节点颜色,并且将旋转后的左右节点染为黑色。比如我们删除 88。
    

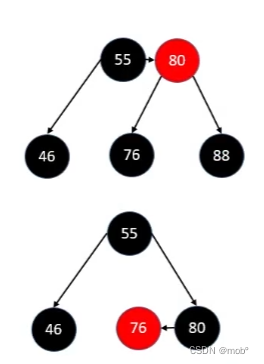
  • 如果兄弟节点是黑色且其没有一个红色子节点且父节点是红色。 则将父节点（80）进行下溢，并且将兄弟节点（76）染成红色，父节点（80）染成黑色。
    

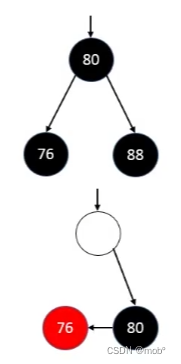
  • 如果兄弟节点是黑色且没有一个红色子节点且父节点是黑色。同样进行下溢，但是要将父节点（80）作为新的被删除节点进行递归调用，继续判断如何调整即可。
    

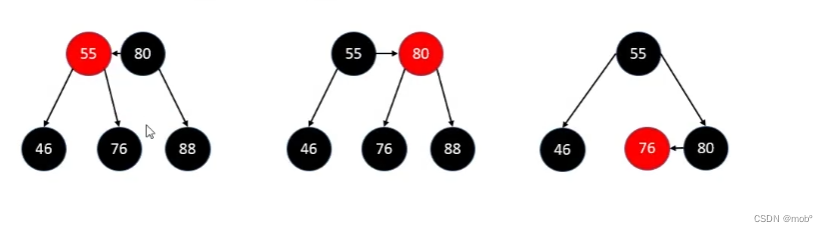
4. 如果 被删除节点为黑色且兄弟节点为红色，可先将兄弟节点染为黑色（55），再将parent节点染为红色。在进行左旋转，之后就可套用上面说的，被删除节点为褐色且兄弟节点为黑色且父节点为红色的情况。
   

• 至此删除的所有情况都列举完了，下面就是代码环节了，我也标注了各个代码出所体现上面所列举的情况。

      /**
       * 删除 value = v 的节点
       *
       * @param v
       * @return
       */
      public V remove(V v){
          RBTreeNode<V> node = findNode(v);
          //没有value = v 的节点
          if (node == null) return null;
          V old = node.value;
          //删除node节点
          deleteNode(node);
          return old;
      }
  
      /**
       * 删除node节点
       *
       * @param node
       */
      public void deleteNode(RBTreeNode<V> node){
          //情况1：如果node节点的度为2
          if (node.left != null && node.right != null){
              //node 的后继节点
              RBTreeNode<V> successor = successor(node);
              node.value = successor.value;
              //装换成删除前驱节点（叶子节点）
              node = successor;
          }
          //被删除的节点的子节点（到这里一定度为1 或 0）
          RBTreeNode<V> replacement = node.isLeft() ? node.left : node.right;
          //情况1：如果度为1
          if (replacement != null){
              //则直接使用子节点替换当前节点即可
              replacement.parent = node.parent;
              if (node.parent == null){
                  root = replacement;
              }else if (node.isLeft()){
                  node.parent.left = replacement;
              }else {
                  node.parent.right = replacement;
              }
              //这个对应情况2，node节点为黑色，且子节点为红色，则使用子节点代替node节点，并染黑即可，染黑在 deleteAfter 里会体现出来
              if (node.color == BLACK){
                  deleteAfter(replacement);
              }
          }else {
              //到这里说明node节点没有子节点了
              //当前就一个node节点
              if (node.parent == null){
                  root = null;
                  return;
              }
              //情况3和4：被删除节点为黑色，调整平衡
              deleteAfter(node);
  
              //删除node节点,node可能调整了位置，比如3.3情况，会发生上溢，所以还需要判断是否为null
              if (node.parent != null){
                  if (node.isLeft()){
                      node.parent.left = null;
                  }else {
                      node.parent.right = null;
                  }
                  node.parent = null;
              }
          }
      }
  
      /**
       * 删除node节点后调整红黑树至平衡
       *
       * @param node
       */
      public void deleteAfter(RBTreeNode<V> node){
          //情况2 ： 也应前面传replacement 的情况，直接染黑返回
          if (isRed(node)){
              node.black();
              return;
          }
          RBTreeNode<V> parent = node.parent;
          //删除的是根节点
          if (parent == null) return;
          //到这里说明node节点是黑色了，继续讨论
          //获取兄弟节点
          RBTreeNode<V> sibling = node.isLeft() ? parent.right : parent.left;
          if (node.isRight()){
              //情况4：被删除节点为黑色，且兄弟节点为红色
              if (isRed(sibling)){
                  sibling.black();
                  parent.red();
                  rightRotate(parent);
                  //旋转之后，兄弟节点变化了，进行更新.之后套用 情况3.2
                  sibling = parent.left;
              }
              //到这里 sibling 必为黑色了
              //情况3.2 和 情况 3.3：被删除节点为黑色，且兄弟节点为黑色，且兄弟节点没有一个红色子节点
              if (isBlack(sibling.left) && isBlack(sibling.right)){
                  //情况3.1：父节点为黑色 （这里的下溢就是染色，并不是B树真正意义的下溢）
                  parent.black();
                  sibling.red();
                  //情况3.2：父节点为红色
                  if (isBlack(parent)){
                      //递归调用
                      deleteAfter(parent);
                  }
              }else {
                  //情况3.1 : 被删除节点node为黑，兄弟节点为黑，且兄弟节点至少有一个红色子节点，则需要判断旋转方向进行旋转即可
                  if (isBlack(sibling.left)){
                      leftRotate(sibling);
                      sibling = parent.left;
                  }
                  //旋转之后新的父节点要继承原先的父节点
                  sibling.color = parent.color;
                  sibling.left.black();
                  parent.black();
                  rightRotate(parent);
              }
          }else {
              //所有旋转反过来
              //情况4：被删除节点为黑色，且兄弟节点为红色
              if (isRed(sibling)){
                  sibling.black();
                  parent.red();
                  leftRotate(parent);
                  //旋转之后，兄弟节点变化了，进行更新.之后套用 情况3.2
                  sibling = parent.right;
              }
  
              //到这里 sibling 必为黑色了
              //情况3.2 和 情况 3.3：被删除节点为黑色，且兄弟节点为黑色，且兄弟节点没有一个红色子节点
              if (isBlack(sibling.left) && isBlack(sibling.right)){
                  //情况3.1：父节点为黑色 （这里的下溢就是染色，并不是B树真正意义的下溢）
                  parent.black();
                  sibling.red();
                  //情况3.2：父节点为红色
                  if (isBlack(parent)){
                      //递归调用
                      deleteAfter(parent);
                  }
              }else {
                  //情况3.1 : 被删除节点node为黑，兄弟节点为黑，且兄弟节点至少有一个红色子节点，则需要判断旋转方向进行旋转即可
                  if (isBlack(sibling.right)){
                      rightRotate(sibling);
                      sibling = parent.right;
                  }
                  //旋转之后新的父节点要继承原先的父节点
                  sibling.color = parent.color;
                  sibling.right.black();
                  parent.black();
                  leftRotate(parent);
              }
          }
      }
  

---

四、完整代码

• 代码也可看看 TreeMap 源码，TreeMap 就是用红黑树实现的。

  package com.example.demo.tree.rbtree;
  
  import java.util.Comparator;
  
  /**
   * 红黑树的简单实现
   */
  public class RBTree<V> {
  
      //红色
      private static final boolean RED = true;
      //黑色
      private static final boolean BLACK = false;
  
      //根节点
      private RBTreeNode<V> root;
  
      //比较器
      private Comparator<V> comparator;
  
      /**
       * 添加元素，红黑树的节点添加，必是往叶子节点上添加新节点
       * 红黑树添加新节点后仍需要满足红黑树的五条性质
       *  1.节点是 RED 或者 BLACK
       *  2.根节点是 BLACK
       *  3.叶子节点（外部节点，空节点）都是 BLACK
       *  4.RED 节点的子节点都是 BLACK
       *      1.RED 节点的 parent 都是 BLACK
       *      2.从根节点到叶子节点的所有路径都包含相同数目的 BLACK 节点
       *  5.从任一的节点到到叶子节点的所有路径都包含相同数目的 BLACK 节点。
       * 我们每次添加节点，都使新添加的节点为 RED，则可直接满足1,2,3,5，只有 4.1不满足，更方便调整，
       * 所以我们都将新添加的元素默认为 RED
       *
       * @param v
       * @return
       */
      public void add(V v){
          //创建新节点且为红色
          RBTreeNode<V> newNode = new RBTreeNode<>(v);
          //如果是第一次插入
          if (root == null){
              root = new RBTreeNode<>(v);;
              //根节点必须染为黑色
              root.black();
              return;
          }
          //不是第一次插入：
          addNode(newNode);
      }
  
      public void addNode(RBTreeNode<V> newNode) {
          //查找应该插入到哪个叶子节点下面
          RBTreeNode<V> parentNode = findParentNode(root, newNode.value);
          int comp = compare(parentNode.value,newNode.value);
          //插入新节点
          newNode.parent = parentNode;
          if (comp > 0){
              parentNode.left = newNode;
          }else {
              parentNode.right = newNode;
          }
          if (!parentNode.color){
              //1.如果父节点为黑色，则直接插入
              return;
          }
          //2.如果父节点是 RED，且 uncle 节点是 BLACK
          RBTreeNode<V> grand = parentNode.parent;
          if (grand != null){
              if (!parentNode.uncle()){
                  if (parentNode.isRight()){// right
                      if(comp > 0){ // Left
                          // 右旋
                          rightRotate(parentNode);
                          // 左旋
                          leftRotate(grand);
                      }else { // right
                          // 左旋
                          leftRotate(parentNode);
                      }
                  }else { // Left
                      if(comp > 0){// left
                          // 右旋
                          rightRotate(parentNode);
                      }else { // right
                          // 左旋
                          leftRotate(parentNode);
                          // 右旋
                          rightRotate(grand);
                      }
                  }
                  return;
              }
              //3.如果父节点是 RED，且 uncle 节点是 RED
              //上溢
              upOverFlow(newNode);
          }
      }
  
  
      /**
       * 删除 value = v 的节点
       *
       * @param v
       * @return
       */
      public V remove(V v){
          RBTreeNode<V> node = findNode(v);
          //没有value = v 的节点
          if (node == null) return null;
          V old = node.value;
          //删除node节点
          deleteNode(node);
          return old;
      }
  
      /**
       * 返回 node 的后继节点
       *
       * @param node
       * @return
       */
      public RBTreeNode<V> successor(RBTreeNode<V> node){
          RBTreeNode<V> child = node.right;
          if (child == null) return null;
          while (child.left != null){
              child = child.left;
          }
          return child;
      }
  
      /**
       * 删除node节点
       *
       * @param node
       */
      public void deleteNode(RBTreeNode<V> node){
          //情况1：如果node节点的度为2
          if (node.left != null && node.right != null){
              RBTreeNode<V> successor = successor(node);
              node.value = successor.value;
              //装换成删除前驱节点（叶子节点）
              node = successor;
          }
          //被删除的节点的子节点（到这里一定度为1 或 0）
          RBTreeNode<V> replacement = node.isLeft() ? node.left : node.right;
          //情况1：如果度为1
          if (replacement != null){
              //则直接使用子节点替换当前节点即可
              replacement.parent = node.parent;
              if (node.parent == null){
                  root = replacement;
              }else if (node.isLeft()){
                  node.parent.left = replacement;
              }else {
                  node.parent.right = replacement;
              }
              //这个对应情况2，node节点为黑色，且子节点为红色，则使用子节点代替node节点，并染黑即可，染黑在 deleteAfter 里会体现出来
              if (node.color == BLACK){
                  deleteAfter(replacement);
              }
          }else {
              //到这里说明node节点没有子节点了
              //当前就一个node节点
              if (node.parent == null){
                  root = null;
                  return;
              }
              //情况3和4：被删除节点为黑色，调整平衡
              deleteAfter(node);
  
              //删除node节点,node可能调整了位置，比如3.3情况，会发生上溢，所以还需要判断是否为null
              if (node.parent != null){
                  if (node.isLeft()){
                      node.parent.left = null;
                  }else {
                      node.parent.right = null;
                  }
                  node.parent = null;
              }
          }
      }
  
      /**
       * 删除node节点后调整红黑树至平衡
       *
       * @param node
       */
      public void deleteAfter(RBTreeNode<V> node){
          //情况2 ： 也应前面传replacement 的情况，直接染黑返回
          if (isRed(node)){
              node.black();
              return;
          }
          RBTreeNode<V> parent = node.parent;
          //删除的是根节点
          if (parent == null) return;
          //到这里说明node节点是黑色了，继续讨论
          //获取兄弟节点
          RBTreeNode<V> sibling = node.isLeft() ? parent.right : parent.left;
          if (node.isRight()){
              //情况4：被删除节点为黑色，且兄弟节点为红色
              if (isRed(sibling)){
                  sibling.black();
                  parent.red();
                  rightRotate(parent);
                  //旋转之后，兄弟节点变化了，进行更新.之后套用 情况3.2
                  sibling = parent.left;
              }
              //到这里 sibling 必为黑色了
              //情况3.2 和 情况 3.3：被删除节点为黑色，且兄弟节点为黑色，且兄弟节点没有一个红色子节点
              if (isBlack(sibling.left) && isBlack(sibling.right)){
                  //情况3.1：父节点为黑色 （这里的下溢就是染色，并不是B树真正意义的下溢）
                  parent.black();
                  sibling.red();
                  //情况3.2：父节点为红色
                  if (isBlack(parent)){
                      //递归调用
                      deleteAfter(parent);
                  }
              }else {
                  //情况3.1 : 被删除节点node为黑，兄弟节点为黑，且兄弟节点至少有一个红色子节点，则需要判断旋转方向进行旋转即可
                  if (isBlack(sibling.left)){
                      leftRotate(sibling);
                      sibling = parent.left;
                  }
                  //旋转之后新的父节点要继承原先的父节点
                  sibling.color = parent.color;
                  sibling.left.black();
                  parent.black();
                  rightRotate(parent);
              }
          }else {
              //所有旋转反过来
              //情况4：被删除节点为黑色，且兄弟节点为红色
              if (isRed(sibling)){
                  sibling.black();
                  parent.red();
                  leftRotate(parent);
                  //旋转之后，兄弟节点变化了，进行更新.之后套用 情况3.2
                  sibling = parent.right;
              }
  
              //到这里 sibling 必为黑色了
              //情况3.2 和 情况 3.3：被删除节点为黑色，且兄弟节点为黑色，且兄弟节点没有一个红色子节点
              if (isBlack(sibling.left) && isBlack(sibling.right)){
                  //情况3.1：父节点为黑色 （这里的下溢就是染色，并不是B树真正意义的下溢）
                  parent.black();
                  sibling.red();
                  //情况3.2：父节点为红色
                  if (isBlack(parent)){
                      //递归调用
                      deleteAfter(parent);
                  }
              }else {
                  //情况3.1 : 被删除节点node为黑，兄弟节点为黑，且兄弟节点至少有一个红色子节点，则需要判断旋转方向进行旋转即可
                  if (isBlack(sibling.right)){
                      rightRotate(sibling);
                      sibling = parent.right;
                  }
                  //旋转之后新的父节点要继承原先的父节点
                  sibling.color = parent.color;
                  sibling.right.black();
                  parent.black();
                  leftRotate(parent);
              }
          }
      }
  
      /**
       * 左旋 将node 和 子节点进行旋转，达到 node节点位置降低，而子节点位置上升的效果
       *
       * @param node
       */
      public void leftRotate(RBTreeNode<V> node) {
          //父节点
          RBTreeNode<V> parent = node.parent;
          //grand 节点
          RBTreeNode<V> grand = parent.parent;
          //左节点
          RBTreeNode<V> left = node.left;
          //1. 将 grand 节点 的 子节点指向 node 节点
          if (grand == null){
            root = node;
            node.black();
          } else if (parent.isLeft()){
              grand.left = node;
          }else {
              grand.right = node;
          }
          //2. 将 node 的父节点 指向 grand 节点
          node.parent = grand;
          //3. 将 node 节点的左节点指向 parent 节点
          node.left = parent;
          //4. 将 parent 节点的 parent 指向 node 节点
          parent.parent = node;
          //5. 将 parent 节点的 right 指向 node 的left
          parent.right = left;
          //6. 将 node 节点的left 节点的parent 指向 parent 节点
          if (left != null){
              left.parent = parent;
          }
          //7. node 节点染成黑色
          node.black();
          //8. parent 节点染成红色
          if (parent != root){
              parent.red();
          }
  
      }
  
      /**
       * 右旋，将node 和 子节点进行旋转，达到 node节点位置降低，而子节点位置上升的效果
       *
       * @param node
       */
      public void rightRotate(RBTreeNode<V> node){
          //父节点
          RBTreeNode<V> parent = node.parent;
          //grand 节点
          RBTreeNode<V> grand = parent.parent;
          //右节点
          RBTreeNode<V> right = node.right;
          //1. 将 grand 节点 的 左子节点指向 node 节点
          if (grand == null) {
              root = node;
              root.black();
          }else if (parent.isLeft()){
              grand.left = node;
          }else {
              grand.right = node;
          }
          //2. 将 node 的父节点 指向 grand 节点
          node.parent = grand;
          //3. 将 node 节点的右节点指向 parent 节点
          node.right = parent;
          //4. 将 parent 节点的 parent 指向 node 节点
          parent.parent = node;
          //5. 将 parent 节点的 left 指向 node 的right
          parent.left = right;
          //6. 将 node 节点的 right 节点的parent 指向 parent 节点
          if (right != null){
              right.parent = parent;
          }
          //7. node 节点染成黑色
          node.black();
          //8. parent 节点染成红色
          if (parent != root){
              parent.red();
          }
      }
  
      /**
       * 上溢，通过染色达到上溢的效果
       *
       * @param node
       */
      public void upOverFlow(RBTreeNode<V> node){
          if (!node.parent.color || !node.uncle()) return;
          //父节点
          RBTreeNode<V> parent = node.parent;
          //grand 节点
          RBTreeNode<V> grand = parent.parent;
          //uncle 节点
          RBTreeNode<V> uncle = parent.brother();
          //1.将 grand 上溢 染成红色
          grand.red();
          //2.将parent 染成黑色
          parent.black();
          //3.将 parent 的brother 染成黑色
          uncle.black();
          //4. 以 grand 位新插入的节点，继续向上调整
          addNode(grand);
      }
  
      public RBTreeNode<V> findParentNode(RBTreeNode<V> node,V v){
          if (node.leaf()) return node;
          if (compare(v,node.value) < 0){
              return findParentNode(node.left,v);
          }else {
              return findParentNode(node.right,v);
          }
      }
  
  
      /**
       * 判断节点node 是否为黑色，空节点也为黑色
       *
       * @param node
       * @return
       */
      public boolean isBlack(RBTreeNode<V> node){
          return node == null || node.color == BLACK;
      }
  
      /**
       * 判断节点 node 是否为红色，空节点为黑色
       * @param node
       * @return
       */
      public boolean isRed(RBTreeNode<V> node){
          return node != null && node.color == RED;
      }
  
      /**
       * 查找值我 v 的节点
       *
       * @param v
       * @return
       */
      public RBTreeNode<V> findNode(V v){
          RBTreeNode<V> node = root;
          while (node != null){
              int comp = compare(node.value,v);
              if (comp < 0){
                  node = node.right;
              }else if (comp > 0){
                  node = node.left;
              }else {
                  return node;
              }
          }
          return null;
      }
  
      private int compare(V a, V b){
          if (comparator == null){
              return ((Comparable<V>)a).compareTo(b);
          }
          return comparator.compare(a,b);
      }
  
      /**
       * 红黑树的节点
       *
       * @param <V> 节点存储的值类型
       */
      private static class RBTreeNode<V>{
          //节点存储的值
          private V value;
          //节点颜色
          private boolean color;
          //左子节点
          private RBTreeNode<V> left;
          //右子节点
          private RBTreeNode<V> right;
          //父节点
          private RBTreeNode<V> parent;
          public RBTreeNode(V v){
              this.value = v;
              //新建的节点默认是红色
              this.color = RED;
          }
  
          public RBTreeNode(V v, boolean color){
              this.value = v;
              this.color = color;
          }
  
          public boolean colorOf(){
              return color;
          }
  
          /**
           * 返回节点的颜色
           *
           * @return
           */
          public boolean color(){
              return color;
          }
  
          /**
           * 将节点染成红色
           *
           * @return
           */
          public void red(){
              this.color = RED;
          }
  
          /**
           * 将节点染成黑色
           */
          public void black(){
              this.color = BLACK;
          }
  
          /**
           * 判断是否为叶子节点
           */
          public boolean leaf(){
              return left == null && right == null;
          }
  
          /**
           * 当前节点是否为左节点
           *
           * @return
           */
          public boolean isLeft(){
              return parent != null && this == parent.left;
          }
  
          /**
           * 当前节点是否为右节点
           *
           * @return
           */
          public boolean isRight(){
              return parent != null && this == parent.right;
          }
  
          public RBTreeNode<V> brother(){
              return this == parent.left ? parent.right: parent.left;
          }
          /**
           * 返回叔父节点的颜色，如果我空，则是黑色
           *
           * @return
           */
          public boolean uncle(){
              if (isLeft()){
                  return parent.right == null ? BLACK: parent.right.color;
              }else {
                  return parent.left == null ? BLACK: parent.left.color;
              }
          }
  
          @Override
          public String toString() {
              String str = "";
              if (color == RED){
                  str = "R_";
              }
              return str;
          }
      }
  }
  
  

总结

• 红黑树 于 AVL 树对比
  

• 理论看再多不如自己动手实现一遍，才能体会到很多没注意到的细节。

参考资料：
小破站的小码哥红黑树讲解