政安晨：【深度学习神经网络基础】（二）—

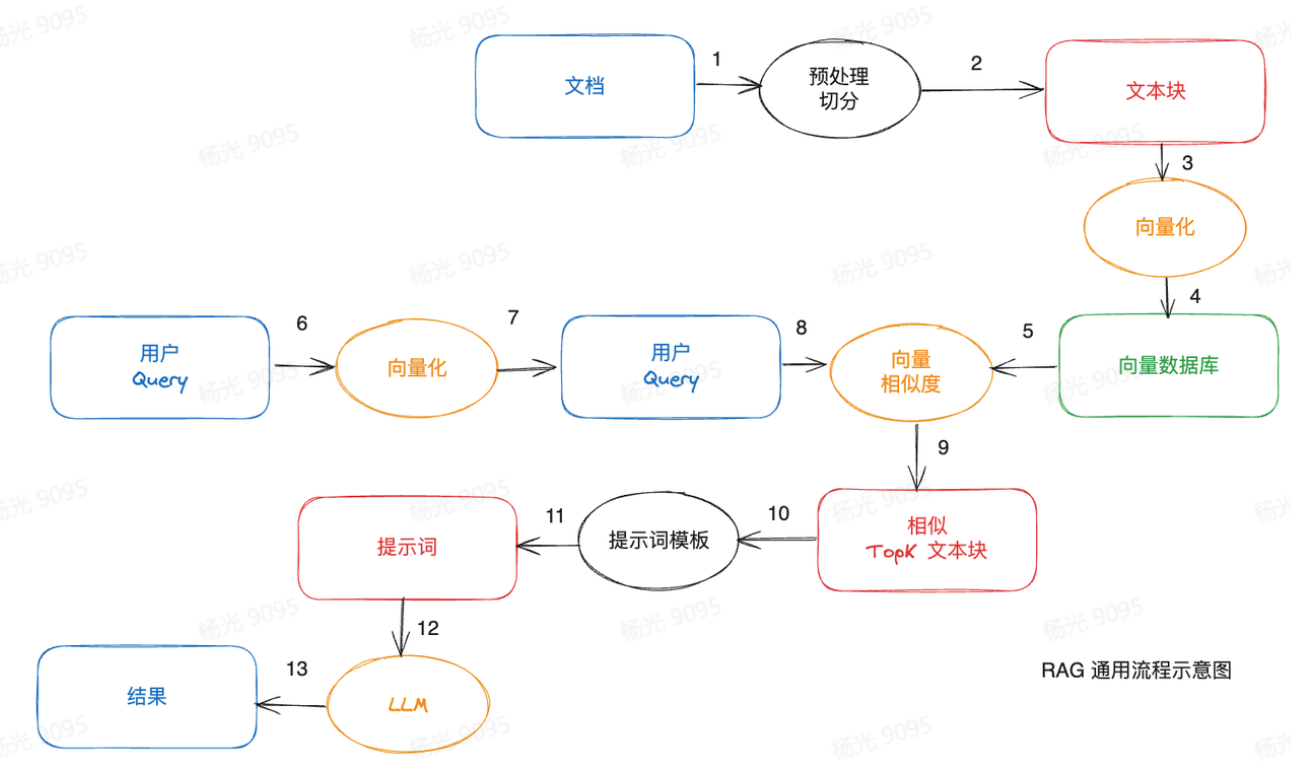
政安晨的个人主页：政安晨

欢迎 👍点赞✍评论⭐收藏

收录专栏: 政安晨的机器学习笔记

希望政安晨的博客能够对您有所裨益，如有不足之处，欢迎在评论区提出指正！

神经元是深度学习神经网络中的基本单元，模拟了生物神经系统中的神经元。

它接收输入信号，并通过激活函数进行非线性转换，然后将转换后的信号传递给下一层神经元或输出。神经元具有一组可学习的权重，它们用于加权输入信号。

神经网络的层是由多个神经元组成的，这些神经元之间相互连接。

在神经网络中，通常有输入层、隐藏层和输出层。输入层接收外部输入数据，并将其传递给下一层。隐藏层是介于输入层和输出层之间的层，根据不同的网络结构可以有多个隐藏层。输出层则产生最终的预测结果。

神经元与层的组织方式使得神经网络可以进行复杂的非线性函数逼近和模式识别。通过对不同层的神经元的权重进行训练优化，神经网络可以学习到输入数据的复杂特征，并根据这些特征进行预测或分类。深度学习神经网络的好处之一就是能够通过增加网络的深度和神经元的数量来提高模型的表达能力和性能。

神经元

大多数神经网络结构使用某种类型的神经元。存在许多结构不同的神经网络，程序员一直在引入实验性的神经网络结构。即便如此，也不可能涵盖所有的神经网络结构。但是，神经网络实现之间存在一些共性。如果一个算法被称为神经网络，那么它通常将由单独的、相互连接的单元组成，尽管这些单元可能被称为神经元，也可能未被称为神经元。实际上，神经网络处理单元的名称在不同的文献中有所不同，它可以被称为节点、神经元或单元。

下图展示了单个人工神经元的抽象结构。

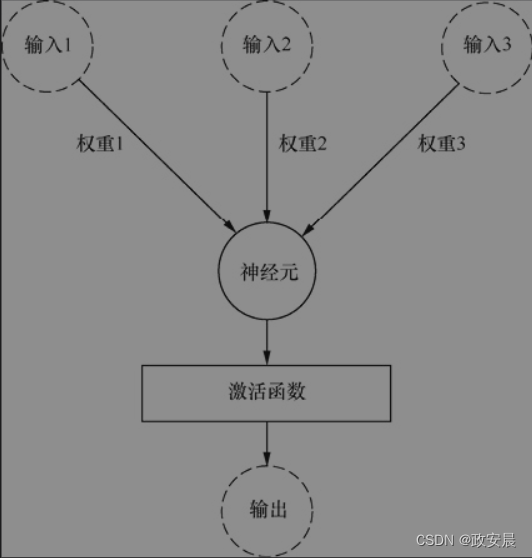
人工神经元从一个或多个来源接收输入，该来源可以是其他神经元，也可以是计算机程序提供给该网络的数据。

输入通常是浮点数或二元值。通常将真（true）和假（false）表示为1和0，从而将二元值输入编码为浮点数。有时，程序还将二元值输入编码体现为双极性系统，即将真表示为1，假表示为−1。

人工神经元将每个输入乘以权重。然后，将这些乘积相加，并将和传递给激活函数。有些神经网络不使用激活函数。

下面公式总结了神经元的计算输出：

在上面公式中，变量x和代w表神经元的输入和权重。变量i代表权重和输入的数量。输入的数量和权重的数量必须总是相同的。每个权重乘以其各自的输入，然后将这些乘积乘以一个激活函数，该函数由希腊字母φ（phi）表示。这个过程使神经元只有单个输出。

上图展示了只有一个构建块的结构。你可以将许多人工神经元链接在一起，构建人工神经网络。也可以将人工神经元视为构建块，将输入和输出圆圈视为连接块。

下图展示了由3个神经元组成的简单人工神经网络：

（简单人工神经网络）

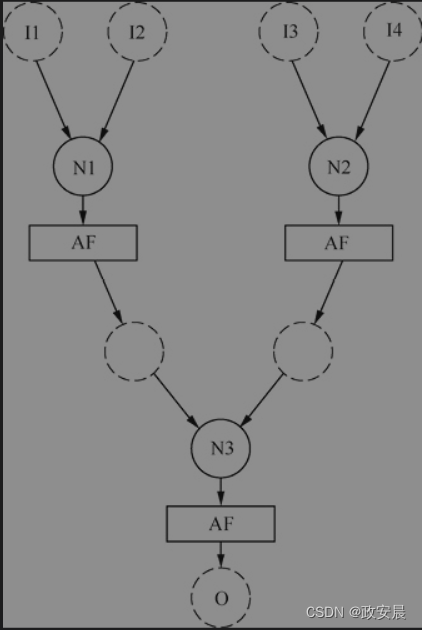
上图展示了3个相互连接的神经元。这个图的本质是，上上张图中减去一些输入，重复3次然后连接。它总共有4个输入和1个输出。神经元N1和N2的输出提供给N3，以产生输出O。为计算上图的输出，我们执行3次上面列出的公式。前两次计算N1和N2，第三次使用N1和N2的输出来计算N3。

神经网络通常不会显示到如上图那样的详细程度。为了简化该图，我们可以省略激活函数和中间输出。简化的人工神经网络如下图所示：

（简化的人工神经网络）

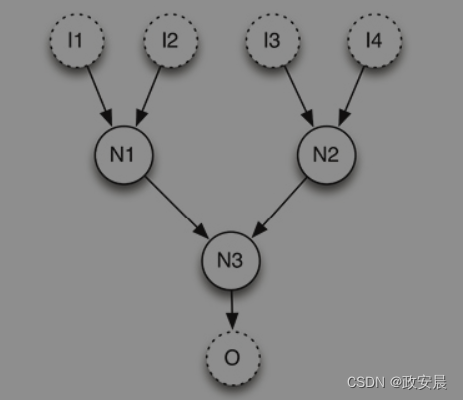
在上图中，你会看到神经网络的两个附加组件。

首先，考虑输入和输出，它们显示为抽象的虚线圆。输入和输出可以是更大的神经网络的一部分。但是，输入和输出通常是特殊类型的神经元，输入神经元从使用该神经网络的计算机程序接收数据，而输出神经元会将结果返回给程序。这种类型的神经元称为输入神经元和输出神经元。

我们将在后面的文章中讨论这些神经元。

上图还展示了神经元的分层排列。

层

输入神经元是第一层，N1和N2神经元创建了第二层，第三层包含N3，第四层包含O。尽管大多数神经网络将神经元排列成层，但并非总是如此。Stanley（2002）引入了一种神经网络架构，称为“增强拓扑神经进化”（NeuroEvolution of Augmenting Topologies，NEAT）。NEAT神经网络可以具有非常杂乱的非分层架构。

形成一层的神经元具有几个特征。

首先，层中的每个神经元具有相同的激活函数。但是，不同的层可能具有不同的激活函数。

其次，各层完全连接到下一层。换言之，一层中的每个神经元都与上一层中的每个神经元有连接。上图所示网络不是完全连接的，有几层缺少连接，如I1和N2不连接。下图所示神经网络是上图的新版本，它已完全连接，并多了一个神经元N4。

（完全连接的神经网络）

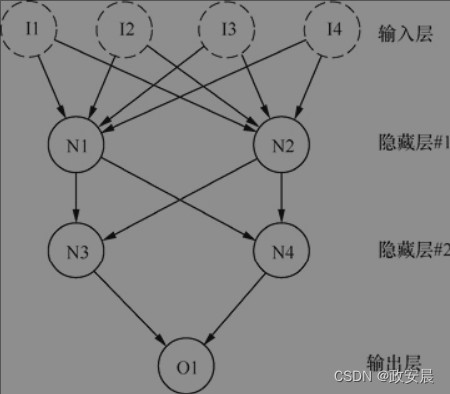
在上图中，你可以看到一个完全连接的多层神经网络。神经网络总是有输入层和输出层。隐藏层的数量决定了神经网络结构的名称。上图中所示的神经网络是一个两层神经网络。大多数神经网络有0～2个隐藏层。除非你实现了深度学习策略，否则很少有具有两个以上隐藏层的神经网络。你可能还会注意到，箭头始终从输入指向输出，向下或向前。这种类型的神经网络通常称为“前馈神经网络”。在咱们这个系列文章的后面，我们将看到在神经元之间形成反向循环的循环神经网络。

神经元的类型

上面咱们简要介绍了存在不同类型的神经元的思想。现在，我们将解释文中描述的所有神经元类型。

并非每个神经网络都会使用每种类型的神经元。单个神经元也有可能扮演几种不同神经元类型的角色：

输入和输出神经元

几乎每个神经网络都有输入和输出神经元。

输入神经元接收来自程序的神经网络数据。

输出神经元将处理后的数据从神经网络返回给程序。

这些输入和输出神经元将由程序分组为单独的层，分组后的层称为输入和输出层。但是，对于某些神经网络结构，神经元可以同时充当输入和输出。霍普菲尔德神经网络就是这样的一个示例，其中神经元既是输入又是输出，以后咱们会详细介绍。

程序通常将神经网络的输入表示为数组，即向量。向量中包含的元素数量必须等于输入神经元的数量。例如，具有3个输入神经元的神经网络可以接收以下输入向量：

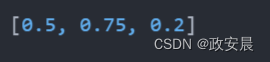
神经网络通常接收浮点数向量作为其输入。同样，神经网络将输出一个向量，其长度等于输出神经元数量。输出通常是来自单个输出神经元的单个值。为了保持一致，我们将单输出神经元网络的输出表示为单个元素的向量。

请注意，输入神经元没有激活函数。如上面第一张图所示，输入神经元只不过是占位符，简单地对输入进行加权和求和。此外，如果神经网络具有既是输入，又是输出的神经元，那么神经网络的输入和输出向量的大小相同。

隐藏神经元

隐藏神经元具有两个重要特征。

首先，隐藏神经元仅接收来自其他神经元的输入，例如输入神经元或其他隐藏神经元。

其次，隐藏神经元仅输出到其他神经元，例如输出神经元或其他隐藏神经元。

隐藏神经元可以帮助神经网络理解输入，并形成输出。但是，它们没有直接连接到输入数据或最终输出。隐藏神经元通常被分组为完全连接的隐藏层。

程序员面临的一个常见问题，就是神经网络中隐藏神经元的数量有多少。由于这个问题的答案很复杂，因此作者的各类文章中多少都有讨论——对隐藏神经元的数量进行相关讨论。在引入深度学习之前，通常人们建议，除了单个隐藏层以外，其他任何东西都是多余的。

研究证明，单层神经网络可以用作通用逼近器（universal approximator）。换言之，只要该神经网络在单层中具有足够的隐藏神经元，它就应该能够学会从任何输入产生（或近似产生）任何输出。

研究者过去忽视其他隐藏层的另一个原因在于，这些层会阻碍神经网络的训练。训练是指确定良好权重的过程。在研究者引入深度学习技术之前，我们根本没有一种有效的方法来训练深度神经网络，即具有大量隐藏层的神经网络。尽管理论上单隐藏层神经网络可以学习任何内容，但深度学习有助于表示数据中更复杂的模式。

偏置神经元

程序员向神经网络添加偏置神经元（bias neurons），以帮助它们学习模式。偏置神经元的功能类似于总是产生值1的输入神经元。由于偏置神经元的输出恒定为1，因此它们没有连接到上一层。值1称为偏置激活，也可以将它设置为1以外的值，但是，1是最常见的偏置激活。并非所有的神经网络都有偏置神经元。

下图展示了带有偏置神经元的单层神经网络。

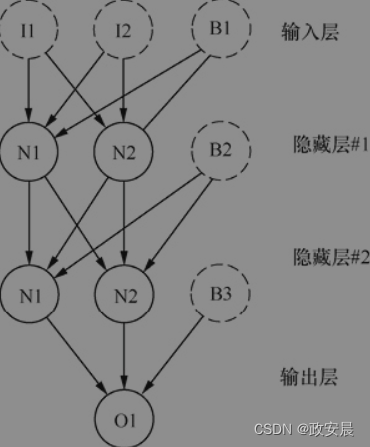
从上图可以看出：除输出层外，每层都包含一个偏置神经元。偏置神经元允许激活函数的输出发生偏移。在以后讨论激活函数时，我们将清楚地看到这种偏移发生的方式。

上下文神经元

上下文神经元用于循环神经网络。

这种类型的神经元允许神经网络保持状态，因此，给定的输入可能并不总是产生完全相同的输出。

这种不一致类似于生物大脑的运作。

请考虑当听到喇叭声时，上下文因素如何影响你的反应。如果你在过马路时听到喇叭声，则可能会感到震惊，停止行走并朝喇叭声传来的方向看。

如果你在电影院观看动作类、冒险类电影时听到喇叭声，你的反应就不会完全一样。

因此，先前的输入为你提供了处理喇叭声输入的上下文。

时间序列是上下文神经元的一种应用。

你可能需要训练神经网络来学习输入信号，从而执行语音识别或预测安全价格的趋势。

上下文神经元是神经网络处理时间序列数据的一种方法。

下图展示了上下文神经元如何在神经网络中排列：

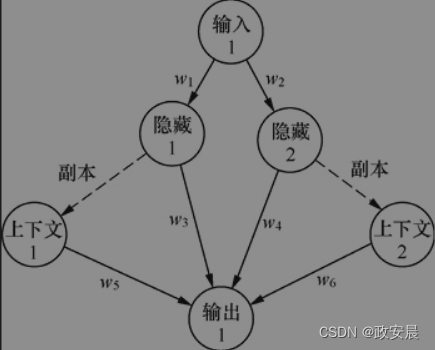
这个神经网络具有单个输入和输出神经元。

在输入层和输出层之间是两个隐藏神经元和两个上下文神经元。除了两个上下文神经元，该神经网络与本文中先前的神经网络相同。

每个上下文神经元都有一个从0开始的值，并且始终从神经网络的先前使用中接收隐藏1或隐藏2的副本。上图中的两条虚线表示上下文神经元是直接副本，没有其他权重。其他线表明输出由列出的6个权重值之一加权。仍然使用上述公式以相同的方式计算输出。输出神经元的值将是所有4个输入分别乘以它们的权重后的总和，并应用激活函数的结果。

有一种神经网络名为简单循环神经网络（Simple Recurrent Neural Network，SRN），它使用了上下文神经元。若当神经网络（Jordan neural network）和埃尔曼网络（Elman neural nebwork）是两种最常见的简单循环神经网络。上图展示了埃尔曼神经网络。

以后咱们应该也会有机会探讨这两种类型的简单循环神经网络。