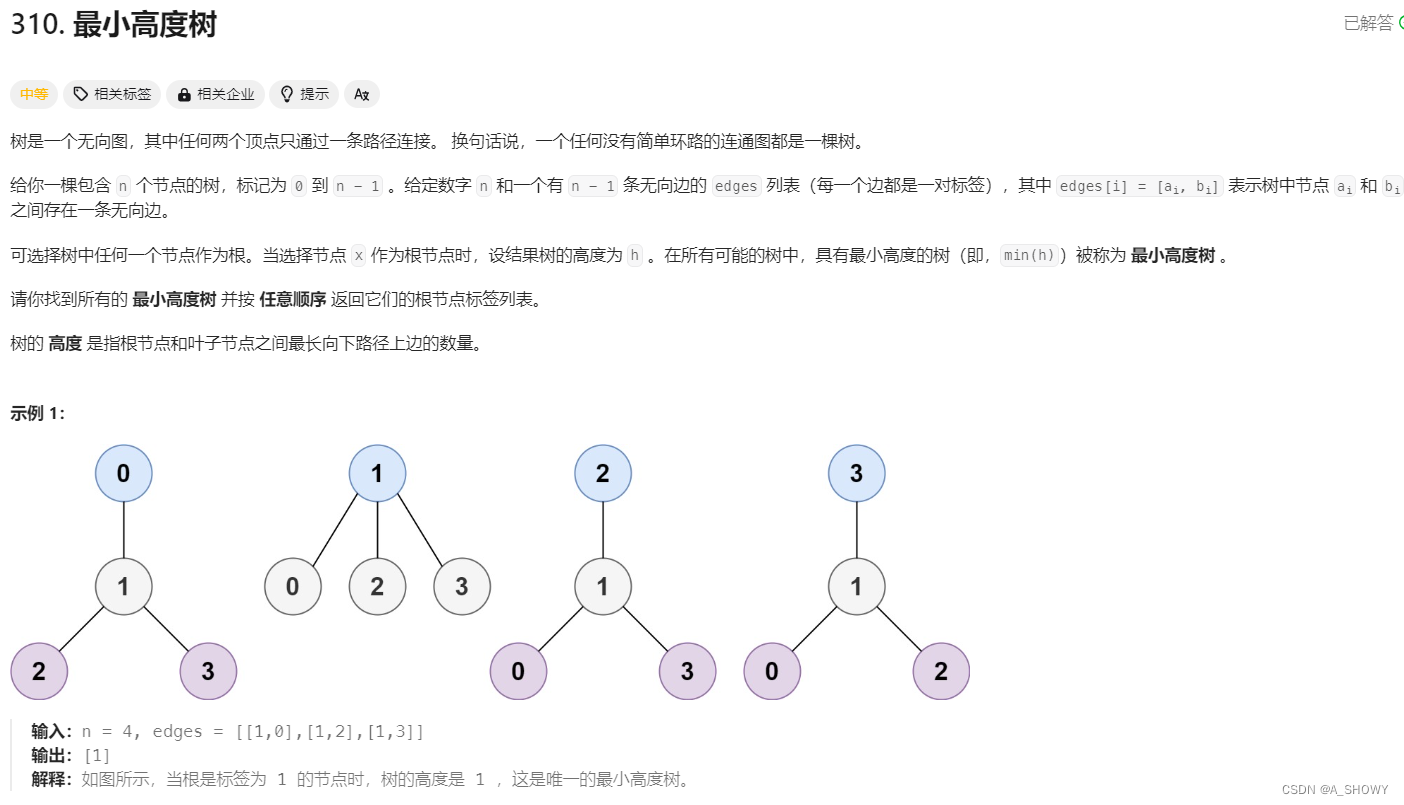
二维动态规划思路：

         首先，刚做完这道题：力扣---最长有效括号---动态规划，栈-CSDN博客，所以会有一种冲动，设立g[i]，表示以第i位为结尾的最长回文子串长度，然后再遍历一遍取最大长度即可。但是，后来发现如果g[i]如此表示，很难得到递推公式。所以转到二维，设立g[i][j]（bool），将其表示以第i位开头第j位结尾的子串是否是回文子串，并用l和r记录到目前为止最长回文子串的左索引和右索引。所以，递推公式为g[i][j]={如果s[i]==s[j]且g[i+1][j-1]是回文子串，则为1}。此时有需要独立判断两种情况：第一种情况是子串长度为1，g[i][i]=1，第二种情况是子串长度为2(j-i==1)，如果s[i]==s[j]，则g[i][j]=2。

        还要说明一点，为什么在二重循环时，i 的顺序是从len-1到0，j 的顺序是从i到len。因为由g[i+1][j-1]推及g[i][j]，所以我们需要先从左下角向右上角开始推，行数(i)从大到小，列数(j)从小到大。

代码：

C++：

class Solution {
public:
    string longestPalindrome(string s) {
        int len=s.size();
        vector<vector<bool>> g(len,vector<bool>(len,false));

        for(int i=0;i<len;i++){g[i][i]=true;}
        int l=0;
        int r=0;

        for(int i=len-1;i>=0;i--){
            for(int j=i;j<len;j++){
                if(s[i]==s[j]){
                    if(j-i==1){
                        g[i][j]=true;
                    }
                    else{
                        if(i+1<len && j-1>=0 && g[i+1][j-1]==true){
                            g[i][j]=true;
                        }
                    }
                }
                if(g[i][j]==true && j-i>r-l){
                    l=i;
                    r=j;
                }
            }
        }
        return s.substr(l,r-l+1);
    }
};

Python：

class Solution:
    def longestPalindrome(self, s: str) -> str:
        len_s=len(s)
        g=[[False for _ in range(len_s)] for _ in range(len_s)]

        for i in range(len_s):
            g[i][i]=True
        l=0
        r=0

        for i in range(len_s-1,-1,-1):
            for j in range(i,len_s):
                if s[i]==s[j]:
                    if j-i==1:
                        g[i][j]=True
                    else:
                        if i+1<len_s and j-1>=0 and g[i+1][j-1]==True:
                            g[i][j]=True
                if g[i][j]==True and j-i>r-l:
                    l=i
                    r=j
        return s[l:r+1]

注意这句话的写法：

g=[[False for _ in range(len_s)] for _ in range(len_s)]