目录

一. .搜索树

1.1 概念

1.2 操作1 查找

 1.3 操作2 插入

1.4 操作3 删除

1.5 性能分析

1.6 和 java 类集的关系

---

 

一. .搜索树

1.1 概念

• 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
• 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
• 它的左右子树也分别为二叉搜索树

 

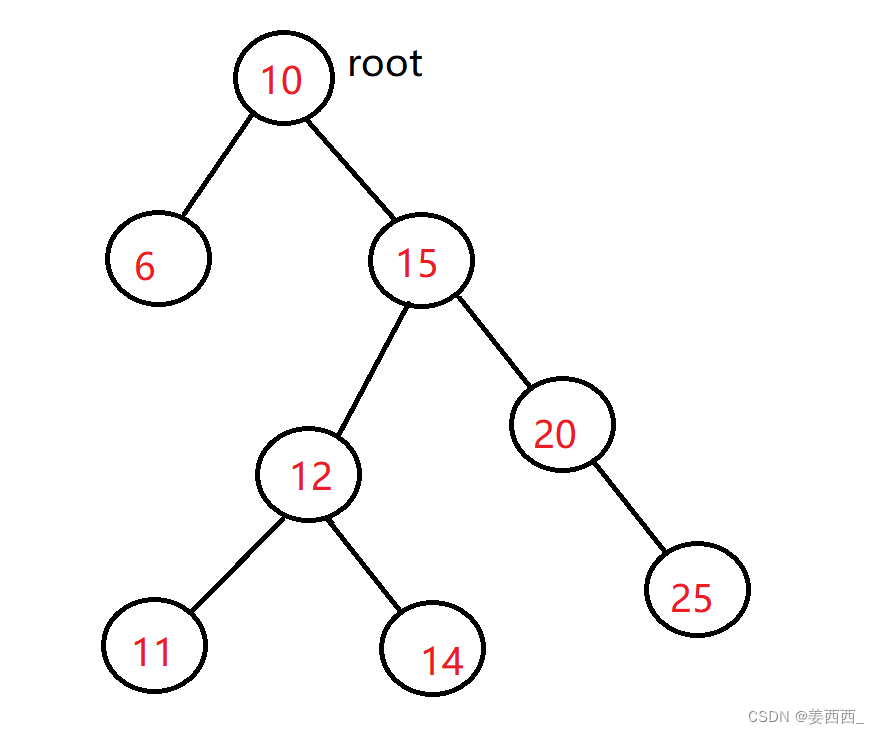
1.2 操作1 查找

思路:

1. 从根节点出发, 如果根节点大于val值, 说明要找的val小于根在根的左边, 所以cur = cur.left
2. 如果根节点小于val值, 说明要找的val大于根在根的右边, 所以cur = cur.right
3. 如果根节点等于val值, 说明找到了, 直接返回true
4. 循环搜索下去, 直到cur == null停止, 说明找不到val值,返回false

 public boolean search(int val){
        TreeNode cur = root;
        while(cur != null){
            if(cur.val > val){
                cur = cur.left;
            }else if(cur.val < val){
                cur = cur.right;
            }else{
                return true;
            }
        }
        return false;
    }

 1.3 操作2 插入

思路:

1. 如果是一颗空树, 直接将结点插入即可
2. 找到合适的位置: 和查找的方法类似, 先循环找到该节点应该插入的位置, 如果根节点大于val值, cur = cur.left, 根节点小于val值, cur = cur.right, 根节点等于val值, 则直接返回, 因为搜索树是不允许有相同的节点的, 直到cur== null, 说明该节点应该插入在此
3. 但是, 如果我们不知道此节点的父亲节点, 那么我们将没法插入, 所以我们要定义一个parent结点, parent始终等于cur的父亲节点
4. 如果val值 < parent.val, 则插入到parent.left, 如果val值 > parent.val, 则插入到parent.right

public void insert(int val){
        if(root == null){
            root = new TreeNode(val);
            return;
        }
        TreeNode node = new TreeNode(val);
        TreeNode cur = root;
        TreeNode parent = null;
        while(cur != null){
            if(cur.val > val){
                parent = cur;
                cur = cur.left;
            }else if(cur.val < val){
                parent = cur;
                cur = cur.right;
            }else{
                return;
            }
        }
        if(parent.val > val){
            parent.left = node;
        }else{
            parent.right = node;
        }
    }

1.4 操作3 删除

思路:

设删除节点为cur, cur的父亲节点为parent

cur结点一共分为三种情况:

情况1. cur.left == null

cur.left == null时, 也分成三种情况:

        1)cur == root, 只需将root = cur.right

        2)cur ! =root && cur == parent.left, 将parent.left = cur.right

        3)cur ! =root && cur == parent.right, 将parent.right = cur.right

情况2. cur.right == null

cur.right == null时, 同样也分成三种情况:(与上面相对应)

        1)cur == root, 只需将root = cur.left

        2)cur ! =root && cur == parent.left,将parent.left = cur.left

        3)cur ! =root && cur == parent.right,将parent.right = cur.left

情况3. cur左右节点都不为空

当cur左右节点都不为空时, 我们采用的方法是替换法:

法一: 找到cur结点左子树的最大值, 将cur的值替换成这个值, 再将此结点删除

法二: 找到cur结点右子树的最小值, 将cur的值替换成这个值, 再将此结点删除

问题一:为什么要找左子树的最大值或右子树的最小值?

答:

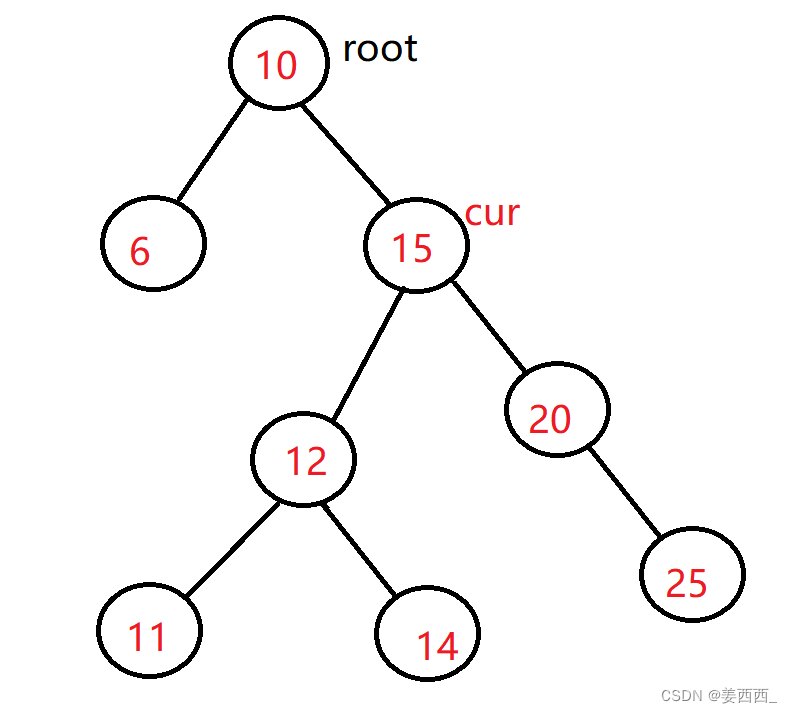
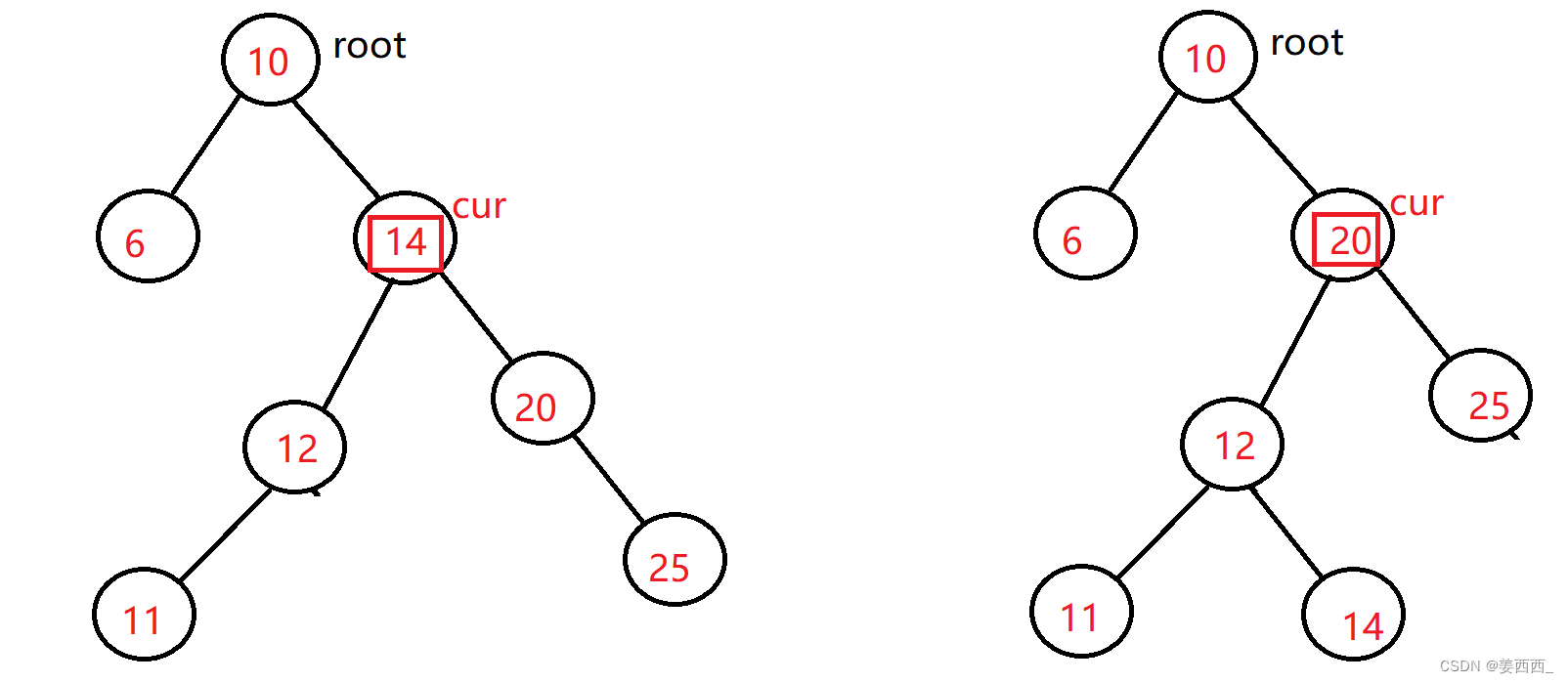
上面这棵树, 删除15, 正常我们要找的14或20, 得到:

可以看到, 替换之后, 依旧满足搜索树的定义, 左子树都比根小, 右子树都比根大

如果我们选择11, 那么:

发现违背了搜索树的定义!

问题二:为什么要使用替换法?

答:假设我们使用法一, 因为此节点时左子树的最大值, 那么说明该节点没有右子树, cur.right == null, 那么删除该节点的方法就非常简单啦, 就是上面的第2种情况

思路(假设使用法一, 找左子树的最大值):

1. 找到要删除的结点cur
2. 找左子树最大值: 定义一个指针t, 令t = cur.left(因为我们要找左子树), 让t去找左子树的最大值, 即如果t有右子树, 则t = t.right, 直到t没有右子树
3. 替换: 此时t为左子树的最大值, 将t.val = cur.val
4. 删除: 还要定义一个tp, 使tp始终等于t的父亲节点, 就回到了情况2: 如果t == tp.left, tp.left = t.left ; 如果t == tp.right, tp.right = t.left

public void remove(int val){
        TreeNode cur = root;
        TreeNode parent = null;
        while(cur != null){
            if(cur.val > val){
                parent = cur;
                cur = cur.left;
            }else if(cur.val < val){
                parent = cur;
                cur = cur.right;
            }else{
                removeNode(parent,cur);
                return;
            }
        }
    }
    public void removeNode(TreeNode parent, TreeNode cur){
//情况1
        if(cur.left == null){
            if(cur == root){
                root = cur.right;
            }else if(cur == parent.left){
                parent.left = cur.right;
            }else if(cur== parent.right){
                parent.right = cur.right;
            }
//情况2
        }else if(cur.right == null){
            if(cur == root){
                root = cur.left;
            }else if(cur == parent.left){
                parent.left = cur.left;
            }else if(cur == parent.right){
                parent.right = cur.left;
            }
//情况3
        }else{
            TreeNode t = cur.left;
            TreeNode tp = cur;
            while(t.right != null){
                tp = t;
                t = t.right;
            }
            cur.val  = t.val;
            if(t == tp.right){
                tp.right = t.left;
            }else{
                tp.left = t.left;
            }
        }
    }

1.5 性能分析