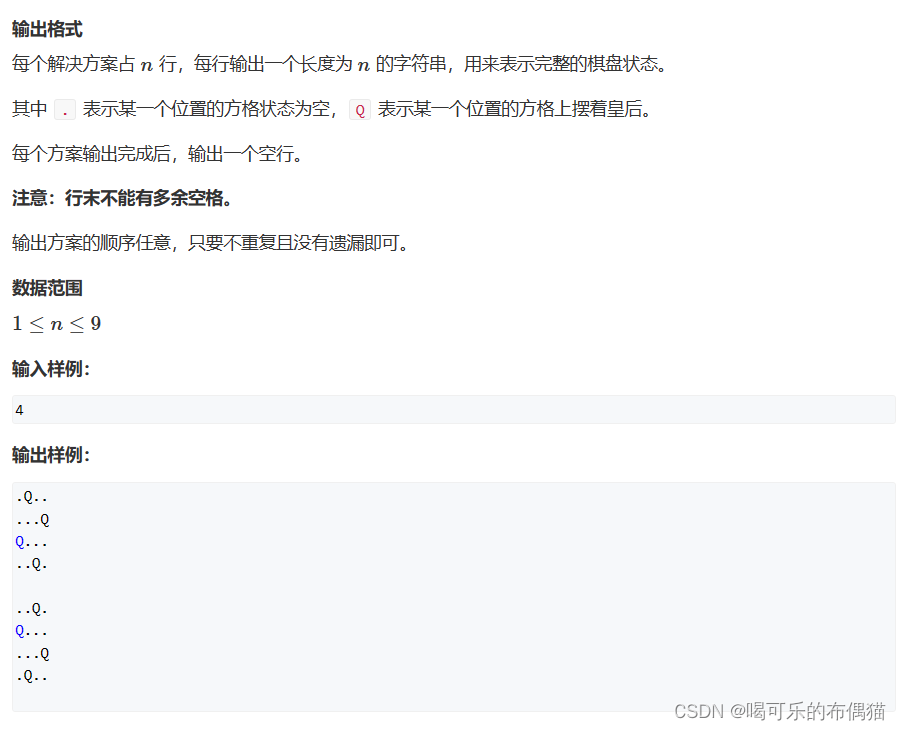
题目描述:

思路:
根据题目要求:即任意两个皇后都不能处于同一行、同一列或同一斜线上。我们可以画图去看一下。对角线之间有什么规律可以发掘出来。接下来请看图解
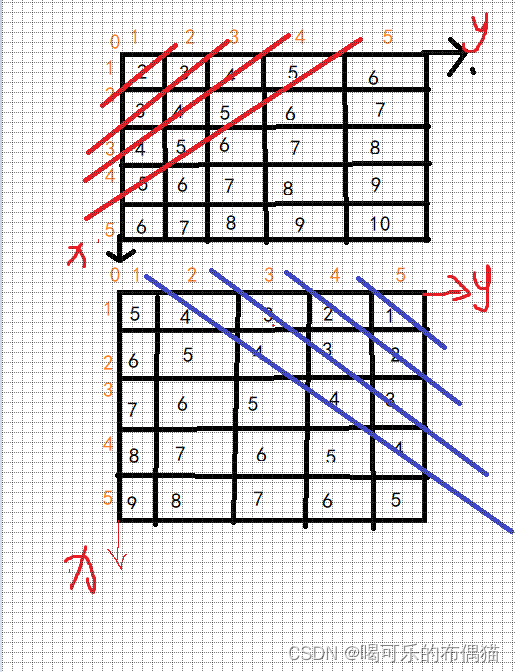
根据上述图片,我们可以把正对角线看成撇对角线,也就是红色线的那个,接下来把反对角线看成是捺对角线,我们可以发现,只要在一个斜线上的数就是一样的,无论是撇对角线,还是捺对角线,这样我们就有了一个条件,还需要保证行和列上不冲突。我们再来往后看看还能发现什么特殊的点呢,如下图

我们其实还可以把所谓的撇对角线,捺对角线类比成一次函数,y = kx+b形式, 固定斜率一个是-1一个是1,那么第一个图中的红色线的就是y = -x + b --> b = x + y
第一个图中蓝线 的部分就是y = x + b ---> b = y - x,由于y-x可能出现负数情况,所以我们加一个偏移量n,这样就变成b = y - x + n。
所以我们把需要创建一个bool型 撇捺数组,把用过且不能的放的点标记上1,两个线确定一个点,此点的撇捺线上都不可以放皇后。

根据第一个图里的数字,我们还可以求出撇捺数组的数据范围是2*n和2*n-1
解法:
此题有两种解法,两种解法的去别在于搜索的顺序不同,第一个解法时间短(按行枚举),第二种解法时间长(每个位置都枚举)。
第一种解法:
我们去按行枚举,也是按照下图(是一个4*4的棋盘)解释,比如我们第一个肯定是先走(1,1)这块,
接着去枚举第二行,第一个位置是(2,1)不行因为列上已经有(1,1)
继续接着走,走到(2,2)这个位置,也不可以,在捺对角线上,
继续走到(2,3),这个点可以。
接着枚举第三行,第一个位置同理不可以,第二个位置(3,2),与(2,3)在同一个撇对角线上不行,接着走(3,4),不可以与(2,3)冲突
所以回到上一个空间也就是第二行,让其接着上次我们走到的(2,3)接着往后走到(2,4),
然后接着去枚举第三行,走着走着,发现(3,2)可以。
那么就第四行,(4,1)这个点和(1,1)冲突,(4,2)和(3,2)冲突,(4,3)和(3,2)冲突,因为在捺对角线上,都不行就回到上一个空间,按照上一个空间皇后的位置接着往后挪,以此类推,这里就不再赘述
通过上面我们可以发现,一 一去枚举行,然后和放皇后的位置,在撇对角线和捺对角线上只要斜线上值相等,那对不起,你不能放这里。
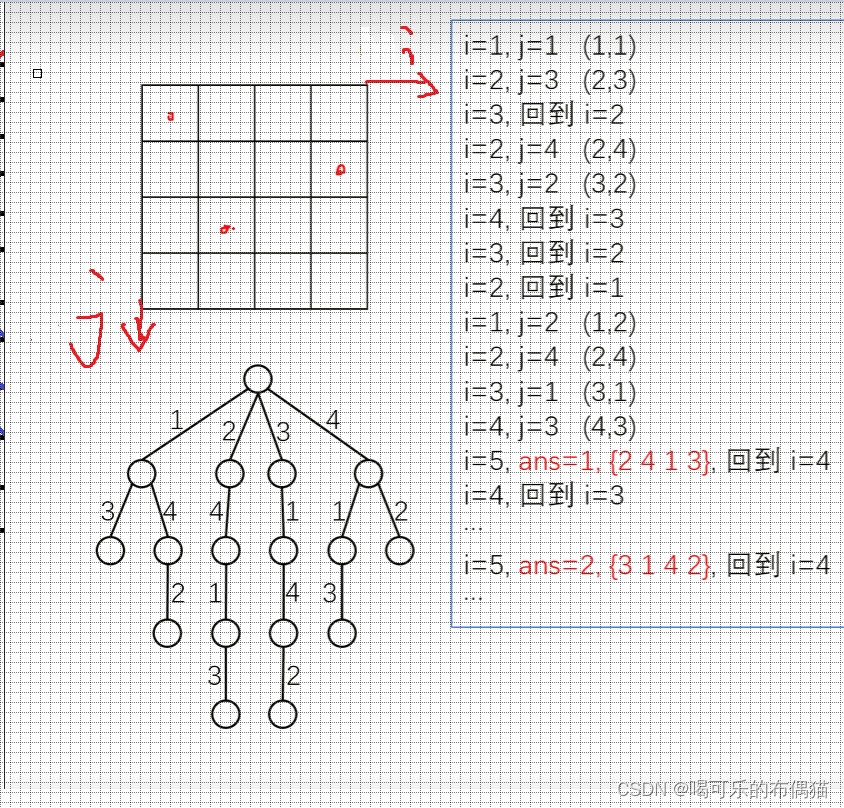
这个树帮助理解,大家按照深度优先搜索去自己走一遍
AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10;
char g[N][N];
//col:列,dg:正下划线,udg:反下划线
bool col[N],dg[N*2],udg[N*2];
int n;
void dfs(int u)
{
//满足情况输出一下
if(u==n)
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout << g[i][j];
}
cout << endl;
}
cout << endl;
return;
}
//枚举列数
for(int i=0;i<n;i++)
{
//行列的映射关系
if(!col[i]&&!dg[i+u]&&!udg[i-u+n])
{
g[u][i] = 'Q';
col[i] = dg[i+u] = udg[i-u+n] = true;
dfs(u+1);
col[i] = dg[i+u] = udg[i-u+n] = false;
g[u][i] = '.';
}
}
}
int main()
{
cin.tie(0)->ios::sync_with_stdio(false);
cin >> n;
//初始化
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
g[i][j] = '.';
}
}
dfs(0);//按行搜索
return 0;
}第二种解法:
这种方法,我们就按照一行一列,一个方块一个方块去枚举,包括每个撇对角线,捺对角线
每一个地方两种情况,根据放还是不放去搜索即可
AC代码:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10;
char g[N][N];
bool col[N*2],row[N*2],dg[N*2],udg[N*2];
int n;
//深搜放和不放
void dfs(int x,int y,int s)
{
//以行为基准,去遍历列相当于一行下遍历n个列
if(y == n) {
y = 0,x++;
}
//n行搜完输出一下结果
if(x == n)
{
if(s == n)//确保皇后全部摆上
{
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
cout << g[i][j];
}
cout << endl;
}
cout << endl;
}
//注意return的位置,不能放在第二个if里,因为假如s不满足就退不回去上一个空间了
return;
}
//不放
dfs(x,y+1,s);
//放
if(!row[x]&&!col[y]&&!dg[x+y]&&!udg[y-x+n])
{
g[x][y] = 'Q';
row[x] = col[y] = dg[x+y] = udg[y-x+n] = true;
dfs(x,y+1,s+1);
//恢复现场
row[x] = col[y] = dg[x+y] = udg[y-x+n] = false;
g[x][y] = '.';
}
}
int main()
{
cin.tie(0)->ios::sync_with_stdio(false);
cin >> n;
//初始化
for(int i=0;i<n;i++)
{
for(int j=0;j<n;j++)
{
g[i][j] = '.';
}
}
//行,列,放皇后的数量
dfs(0,0,0);
return 0;
}以上部分图片来源于B站董晓算法,有的地方是自己的个人理解,如果有错误,欢迎指出,喜欢的小伙伴可以留个关注~
这个题会的可以去做洛谷P1219
推荐AcWing 843. n-皇后问题--图解+代码注释 - AcWing
和哔哩哔哩董晓算法n-皇后问题