目录
一、前言:误差与拟合
(一)经验误差
(二)过拟合、欠拟合
二、评估方法
(一)评估总体的思路
(二)如何划分训练集和测试集
1.留出法
2.k折交叉验证
3.自助法
三、性能度量
(一)均方误差
(二)错误率&精度
(三)查准率&查全率
补充:
(四)F1&Fβ
(五)ROC&AUC
为了实现对模型指导,实现自主建模,我们会对模型进行选择和评估,主要有以下几个问题:

一、前言:误差与拟合
(一)经验误差
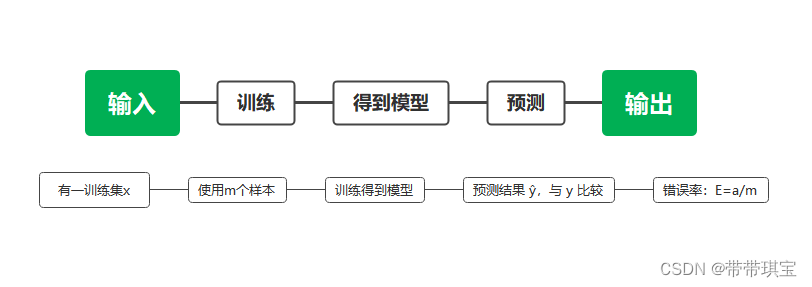
使用上述流程理解,其中 a 为预测错误的个数,m为使用的样本数量,则有以下概念:
- 错误率(error rate):分类错误的样本数占样本总数的比例。即在 m 个样本中有 a 个样本分类错误,则错误率E = a / m。
- 精度(accuracy):精度=1 - a / m ,即 精度 = 1 - 错误率 。
- 误差(error):学习器的预测输出与样本之间的差异。其中:学习器在训练集上的误差称为“训练误差(training error)”或“经验误差(empirical error)”,在新样本上的误差称为“泛化误差(generalization error)”。
(二)过拟合、欠拟合
对于机器学习而言,泛化误差越小越好,但经验误差不一定越小越好,因为会出现“过拟合”问题,西瓜书中就有这样一个例子:
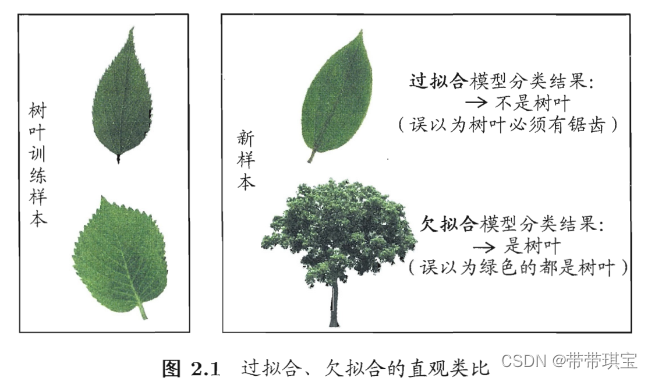
过拟合(overfitting):学习器在训练样本中表现得过于优越,导致在验证数据集以及测试数据集中表现不佳。
可能原因:
- 建模样本选取影响,如样本数量太少,选样方法错误,样本标签错误等,导致选取的样本数据不足以代表预定的分类规则;
- 样本噪音(无关影响因素)干扰,使得机器将部分噪音认为是特征从而扰乱了预设的分类规则;
- 参数太多,模型复杂度过高;
欠拟合(underfitting):可能由于模型过于简单或特征量过少等原因,相对于过拟合,学习器对训练样本的一般性质尚未学好,不能很好地捕捉到数据特征。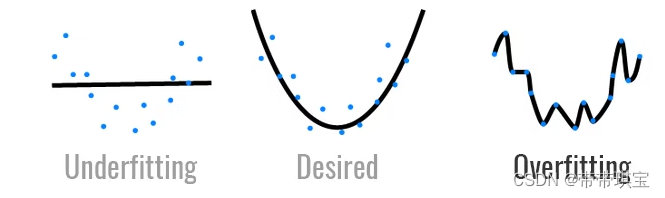
二、评估方法
(一)评估总体的思路
在学习过程中,应尽量减少欠拟合或过拟合对模型的影响,选择泛化误差最小的模型。
泛化误差是无法直接获得的,因此会将数据分为训练集(training set)和测试集(testing set),训练集用于投喂给模型进行学习,而测试集用来“测试”所得到的模型对新样本的泛化能力,然后,以测试集上的“测试误差”(testing error)作为泛化误差的近似。
- 评估方法的关键在于:怎么获得“测试集” (test set)
- 此外可能有些地方会有“验证集”(validation set),验证集的存在一般是为了调节参数
(二)如何划分训练集和测试集
1.留出法
将训练集和测试集简单地37分或28分
注意事项:
- 测试集和训练集在总体中独立同分布,如使用分层采样的方式进行数据划分
- 测试集应该尽可能与训练集互斥
- 通常进行若干次随机划分、重复实验评估取平均值最为评估结果
-
测试集数量不能极端,太大或太小都不合适 ( 如: 1/5~1/3 如此划分)
代码实现:
如对于一个有监督学习,X 为原数据集(如顾客特征),y 为数据对应标签(是否购买某物品),可以使用 train_test_split() 函数进行数据集的划分:
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.25, random_state = 0)函数详细用法参见:python机器学习 train_test_split()函数用法解析及示例 划分训练集和测试集 以鸢尾数据为例 入门级讲解-CSDN博客
2.k折交叉验证
k折交叉验证即将原本数据集分成 k 分,每次取其中一块当测试集,每次的测试结果平均值作为标准
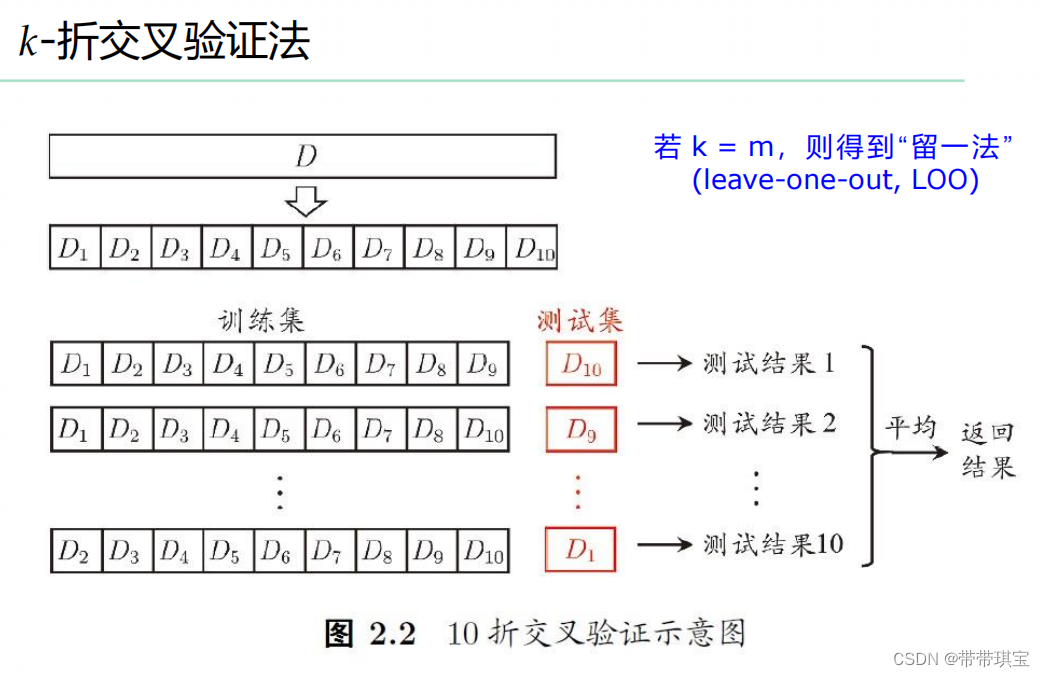
这种方法可以通过 sklearn 中 model_selection 模块的 cross_val_score() 函数实现
例:先生成一个名为 “classifier” 的SVN模型,进行交叉验证后以其均值作为模型精度方差作估计误差
# Fitting Kernel SVM to the Training set
from sklearn.svm import SVC
classifier = SVC(kernel = 'rbf', random_state = 0)
classifier.fit(X_train, y_train)
####################################
# Applying k-Fold Cross Validation #
####################################
from sklearn.model_selection import cross_val_score
#######################################################
# Split training set into 10 folds #
# 10折交叉验证,指定训练模型、数据集、数据标签、迭代次数 #
#######################################################
accuracies = cross_val_score(estimator = classifier, X = X_train, y = y_train, cv = 10)
accuracies.mean() # Get mean as accuracy of model performance
accuracies.std() # Get standard deviation to evaluate variance亦有其他代码可实现,再此不多赘述
补充关于留一法:
直接将样本分成 m 分,每份一个样本,这样做不会受样本划分方式的影响,但在数据量大的情况下对算力有很高要求,结果也未必一定会更准确
3.自助法
该方法通常用于样本量较小的情况,对于含有 m 个数据的样本进行放回抽样,在进行 m 次后,有 36.8% 的样本是不会被取到的,这由以下这个高数中的重要极限得出
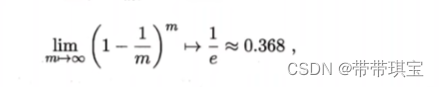
被取到的概率为 1/m,不被取到的概率为 1-1/m,进行 m 次抽取
注意事项:
- 该方法在数据集较小且难以划分时使用
- 会改变数据分布,引入误差
三、性能度量
旨在评价模型的准确度,衡量其泛化能力,实际中什么样的模型是“好”的,不仅取决于算法和数据, 还取决于任务需求
(一)均方误差
对于回归任务,最常用的是均方误差,公式如下:
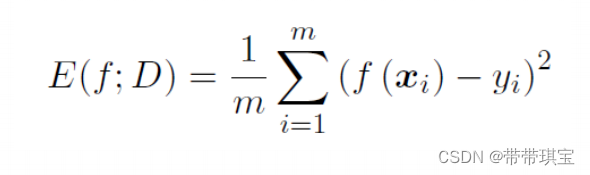
(即:输出值减去实际值平方进行累加后取平均)
字母恐惧的伙伴也别急,这里有解释:
- D:给定的样集D={(x1,y1),(x2,y2),...(xm,xm)},此处为实际的特征 x 和实际标签 y
- m:样集中的样本个数
- f:学习器/模型f
- f(x):模型对于每个 x 输出的预测值
- y:数据中每个 x 对应的实际标签
(二)错误率&精度
这两个指标十分易于理解,也在文章开头就做了介绍,总言之就是模型预测正确的样本及错误样本的占比
(三)查准率&查全率
又称准确率和召回率
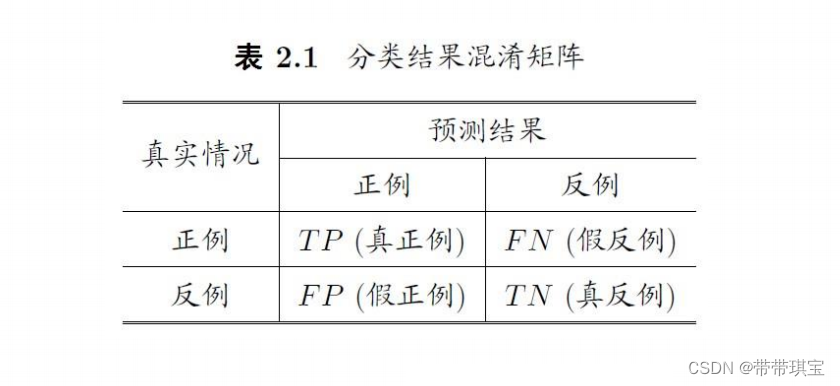
上面这个图叫作混淆矩阵,在实际应用中很有用,先知道几个概念
- 真正例(True Positive):实际结果为positive,模型预测结果也为positive
- 假正例(False Positive):实际结果为negative,模型预测结果却为positive
- 假反例(False Negative):实际结果为positive,模型预测结果却为negative
- 真反例(True Positive):实际结果为negative,模型预测结果也为negative
这里的正反例,比如一个顾客购买了,可以说是正例,某疾病检测结果显示阴性(健康)也可以说是正例,真假则是反应的模型输出结果与实际结果是否一致
此基础上有查准率与查全率公式:

换成人话理解即:
- 查准率=预测正确的的正例占所有预测结果为正例的比例,即所有 f(x) 中的准确率,反应所有预测为正例中正确样本的占比,看查的准不准
如模型预测100人购买,实际上只有75人购买,预测正确,则查准率为75%,有25%被错误地预测为购买
- 查全率=预测正确的的正例占所有实际为正例的比例,反应所有真实正例中被预测正确的占比,就是有没有把它们找出来,查的全不全
如模型预测100位顾客购买,实际上有125人购买,则查全率80%,有20%被错误地预测为未购买
由于FN与FP负相关,查准率和查全率是一对矛盾的度量,两者呈负相关趋势
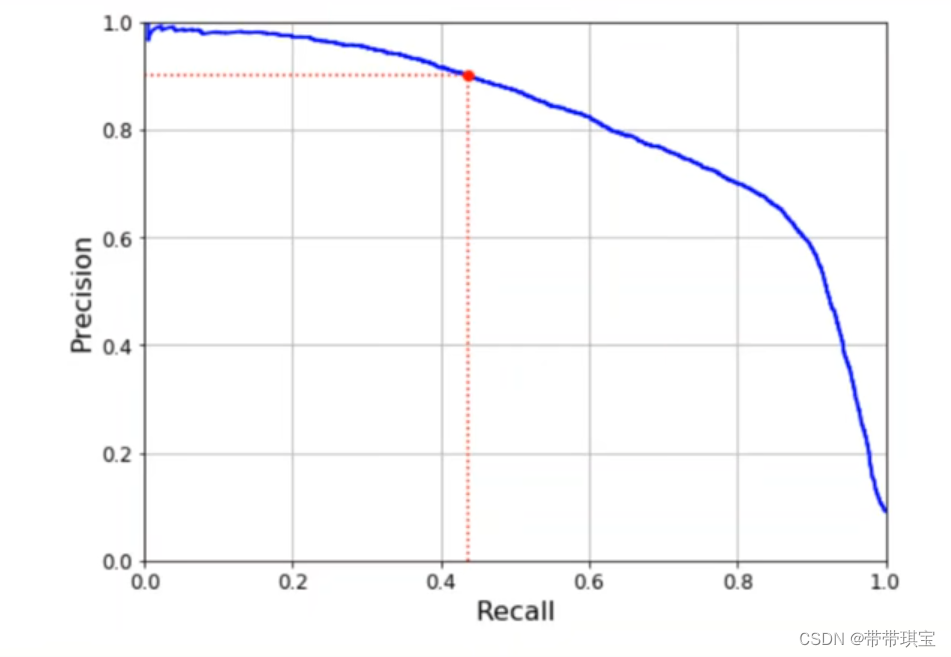
(P-R图像)
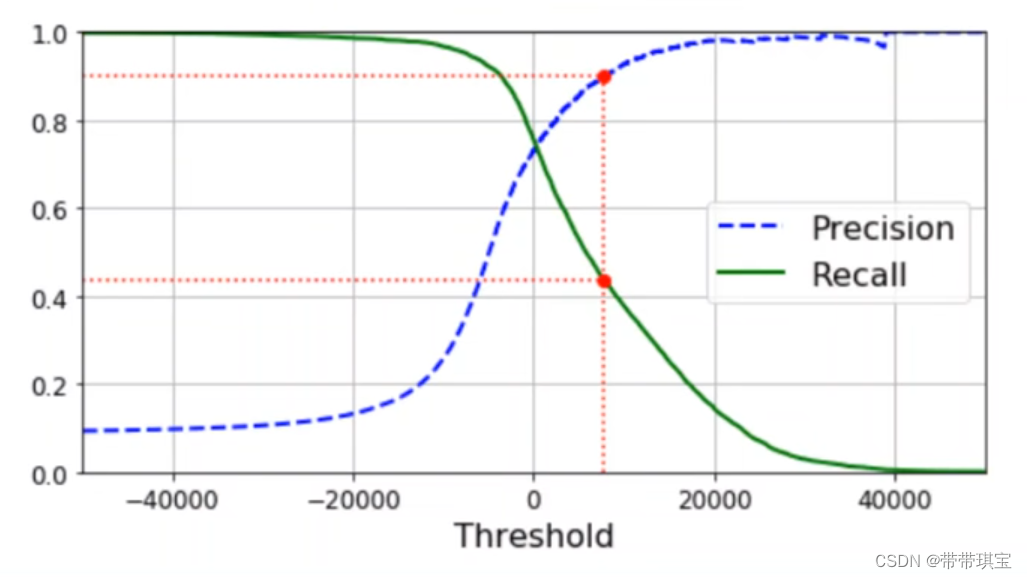
(阈值-PR图像,阈值越小要求低,精确度则越低,找的越全,反之同样道理)
阈值可以大致理解为找出正例的那个标准,关于这两指标的意义文章健康检测的例子举的非常好,可参考【机器学习】模型评估与选择(理论)_提高阈值,查准率查全率-CSDN博客
补充:

平衡点(Break-Event Point,简称 BEP):
是“查准率=查全率”时的取值。如右图中,学习器C的BEP是0.64,而基于BEP的比较,可认为学习器A优于B
模型性能比较:
实际上P-R曲线可以用来比较多个模型的效果,如上图中模型B在任何情况下PR值均比模型C高,效果就比模型C好,那对于模型A和B的比较:
- 比较AB面积
- 根据平衡点进行比较
- 使用指标F1及Fβ
(四)F1&Fβ
由于P与R各有侧重,F1实际上是查全率P与查准率R的加权平均,

则有:

在一些应用中,对查准率和查全率的重视程度有所不同,会对两者进行加权调和平均计算

对于β:
- 𝛽 > 0:度量了查全率对查准率的相对重要性
- 𝛽 = 1:为标准的 𝐹1
- 𝛽 > 1 时查全率 R 有更大影响;𝛽 < 1 时查准率 P 有更大影响
上述问题主要对于单个二分类问题,对于多分类问题,除了直接使用某些算法,也可以看成 n 个二分类问题(one vs one 或 one vs rest),多个二分类问题会产生多个P值、R值,若要衡量总体效果,可以:

(1.先计算再求平均)

(2.先平均再计算)
法2即将多次分类得到的真正例真反例等等个数进行平均,再计算 F 值
(五)ROC&AUC
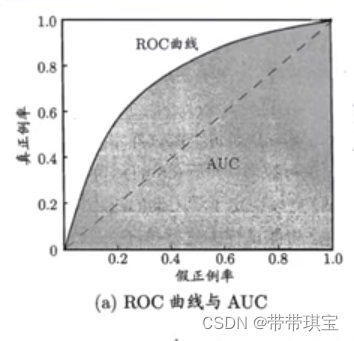
受试者特征曲线 ROC 由以下两部分构成:

TPR 真正利率,其实就是召回率,FPR 假正例率就是反例被错误地分成正例的比率
AUC 即 Area Under Curve,表示一条曲线下面的面积,ROC曲线的AUC值可以用来对模型进行评价。一个纯随机分类器 ROC 曲线下面积是等于 0.5的,可以以此判断一个模型效果如何
同一模型真正例预测出来的越多,假正例自然也会越多,因为总体预测为正例的数量多了
在有实际测试样例时,会得到如下图类似的图像
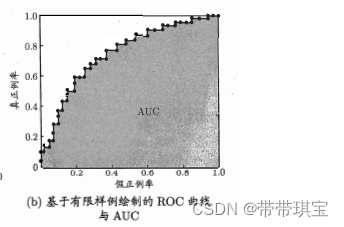
曲线的绘制过程:假设m﹢个正例与m﹣个反例,在得分排序后,阈值最大时所有样例都为反例,即 (0,0),接下来就是移动坐标连线:

每检测出一个真正例或假正例,则在对应轴上增加1/m﹢或1/m﹣,我们一般希望假正例率增加的越慢越好的
关于代价损失、代价敏感错误率与代价曲线部分内容理解还不够深刻,待日后涉及到了再补更