基于BP神经网络的城市空气质量数据预测matlab仿真

news2024/9/20 1:10:19

目录

1.算法运行效果图预览

2.算法运行软件版本

3.部分核心程序

4.算法理论概述

4.1 BP神经网络结构

4.2 神经元模型与激活函数

4.3 前向传播过程

4.4反向传播算法及其误差函数

4.5 权重更新规则

4.6 迭代训练

5.算法完整程序工程

1.算法运行效果图预览

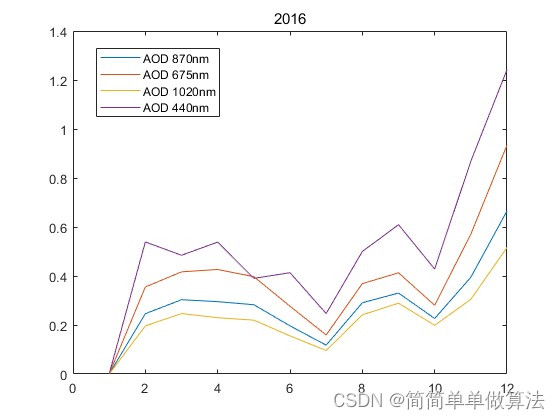
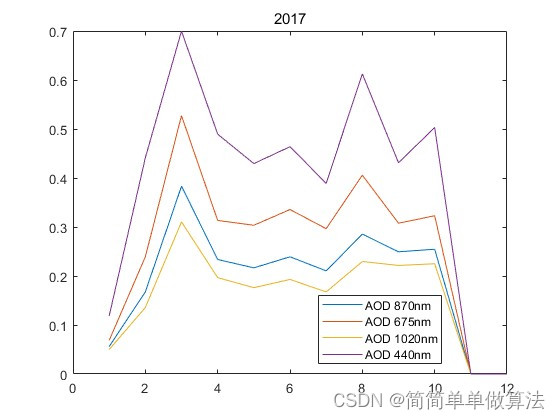
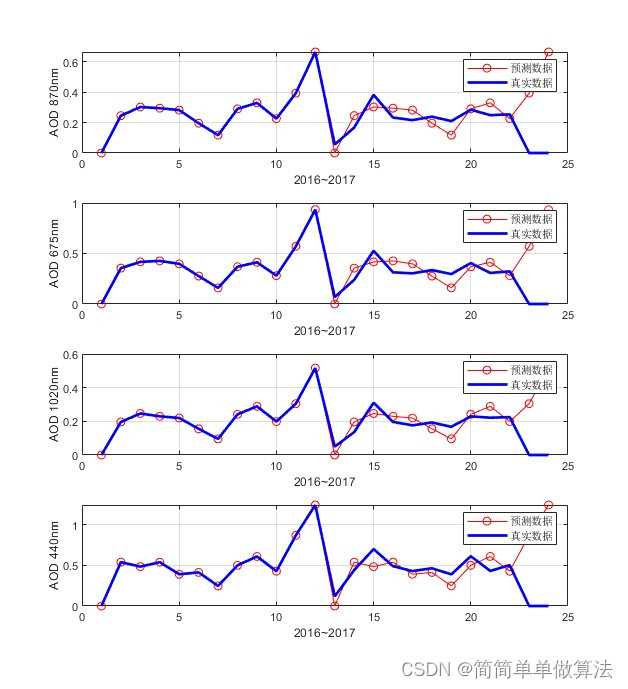
2.算法运行软件版本

matlab2022A

3.部分核心程序

......................................................................................

D2 = dir('data\城市_20160101-20161231\*.csv');
for i = 1:length(D2)
    Name     = ['data\城市_20160101-20161231\',D2(i).name];
    tmps     = csvread(Name,1,3);
    %读取北京数据
    tmps2    = tmps(:,74);
    L        = length(tmps2);
    %15个变量作为一个数据组
    tmps3    = reshape(tmps2',[15,L/15]);
    Data2{i} = mean(tmps3,2);
end
clear tmps tmps2 tmps3


tmp1 = 0;
indx1= 0;
tmp2 = 0;
indx2= 0;
tmp3 = 0;
indx3= 0;
tmp4 = 0;
indx4= 0;
tmp5 = 0;
indx5= 0;
tmp6 = 0;
indx6= 0;
tmp7 = 0;
indx7= 0;
tmp8 = 0;
indx8= 0;
tmp9 = 0;
indx9= 0;
tmp10= 0;
indx10= 0;
tmp11 = 0;
indx11= 0;
tmp12 = 0;
indx12= 0;
for i = 1:length(D1)
    Name     = ['data\城市_20160101-20161231\',D1(i).name];
    month    = str2num(Name(end-7:end-6));
    if month == 1
       tmp1  = tmp1 + Data1{i}; 
       indx1 = indx1 + 1;
    end
    if month == 2
       tmp2  = tmp2 + Data1{i}; 
       indx2 = indx2 + 1;
    end
    if month == 3
       tmp3  = tmp3 + Data1{i}; 
       indx3 = indx3 + 1;
    end
    if month == 4
       tmp4  = tmp4 + Data1{i}; 
       indx4 = indx4 + 1;
    end    
    if month == 5
       tmp5  = tmp5 + Data1{i}; 
       indx5 = indx5 + 1;
    end
    if month == 6
       tmp6  = tmp6 + Data1{i}; 
       indx6 = indx6 + 1;
    end
    if month == 7
       tmp7  = tmp7 + Data1{i}; 
       indx7 = indx7 + 1;
    end
    if month == 8
       tmp8  = tmp8 + Data1{i}; 
       indx8 = indx8 + 1;
    end   
    if month == 9
       tmp9  = tmp9 + Data1{i}; 
       indx9 = indx9 + 1;
    end
    if month == 10
       tmp10  = tmp10 + Data1{i}; 
       indx10 = indx10 + 1;
    end
    if month == 11
       tmp11  = tmp11 + Data1{i}; 
       indx11 = indx11 + 1;
    end
    if month == 12
       tmp12  = tmp12 + Data1{i}; 
       indx12 = indx12 + 1;
    end   
end
%对数据按月划分，计算对应的均值
Data2016 = [tmp1/indx1,tmp2/indx2,tmp3/indx3,tmp4/indx4,tmp5/indx5,tmp6/indx6,tmp7/indx7,tmp8/indx8,tmp9/indx9,tmp10/indx10,tmp11/indx11,tmp12/indx12];


D3 = dir('data\城市_20170101-20171231\*.csv');
for i = 1:length(D3)
    Name     = ['data\城市_20170101-20171231\',D3(i).name];
    tmps     = csvread(Name,1,3);
    %读取北京数据
    tmps2    = tmps(:,74);
    L        = length(tmps2);
    %15个变量作为一个数据组
    tmps3    = reshape(tmps2',[15,L/15]);
    Data3{i} = mean(tmps3,2);
end
clear tmps tmps2 tmps3

tmp1 = 0;
indx1= 0;
tmp2 = 0;
indx2= 0;
tmp3 = 0;
indx3= 0;
tmp4 = 0;
indx4= 0;
tmp5 = 0;
indx5= 0;
tmp6 = 0;
indx6= 0;
tmp7 = 0;
indx7= 0;
tmp8 = 0;
indx8= 0;
tmp9 = 0;
indx9= 0;
tmp10= 0;
indx10= 0;
tmp11 = 0;
indx11= 0;
tmp12 = 0;
indx12= 0;
for i = 1:length(D1)
    Name     = ['data\城市_20170101-20171231\',D1(i).name];
    month    = str2num(Name(end-7:end-6));
    if month == 1
       tmp1  = tmp1 + Data1{i}; 
       indx1 = indx1 + 1;
    end
    if month == 2
       tmp2  = tmp2 + Data1{i}; 
       indx2 = indx2 + 1;
    end
    if month == 3
       tmp3  = tmp3 + Data1{i}; 
       indx3 = indx3 + 1;
    end
    if month == 4
       tmp4  = tmp4 + Data1{i}; 
       indx4 = indx4 + 1;
    end    
    if month == 5
       tmp5  = tmp5 + Data1{i}; 
       indx5 = indx5 + 1;
    end
    if month == 6
       tmp6  = tmp6 + Data1{i}; 
       indx6 = indx6 + 1;
    end
    if month == 7
       tmp7  = tmp7 + Data1{i}; 
       indx7 = indx7 + 1;
    end
    if month == 8
       tmp8  = tmp8 + Data1{i}; 
       indx8 = indx8 + 1;
    end   
    if month == 9
       tmp9  = tmp9 + Data1{i}; 
       indx9 = indx9 + 1;
    end
    if month == 10
       tmp10  = tmp10 + Data1{i}; 
       indx10 = indx10 + 1;
    end
    if month == 11
       tmp11  = tmp11 + Data1{i}; 
       indx11 = indx11 + 1;
    end
    if month == 12
       tmp12  = tmp12 + Data1{i}; 
       indx12 = indx12 + 1;
    end   
end
%对数据按月划分，计算对应的均值
Data2017 = [tmp1/indx1,tmp2/indx2,tmp3/indx3,tmp4/indx4,tmp5/indx5,tmp6/indx6,tmp7/indx7,tmp8/indx8,tmp9/indx9,tmp10/indx10,tmp11/indx11,tmp12/indx12];

save data.mat Data2015 Data2016 Data2017 

data = [Data2015,Data2016,Data2017 ];
figure;
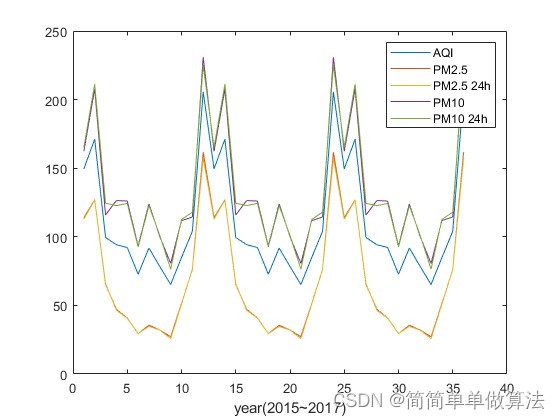
plot(data(1:5,:)');
legend('AQI','PM2.5','PM2.5 24h','PM10','PM10 24h');
xlabel('year(2015~2017)');
figure;
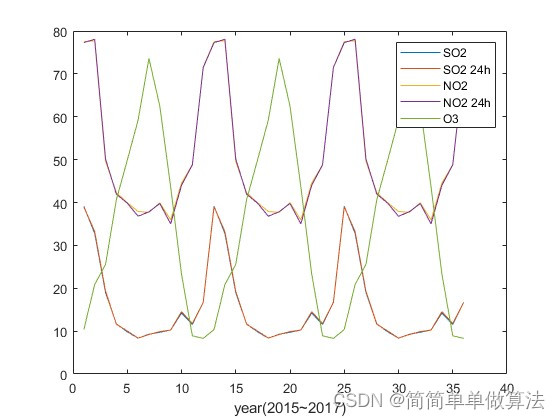
plot(data(6:10,:)');
legend('SO2','SO2 24h','NO2','NO2 24h','O3');
xlabel('year(2015~2017)');
figure;
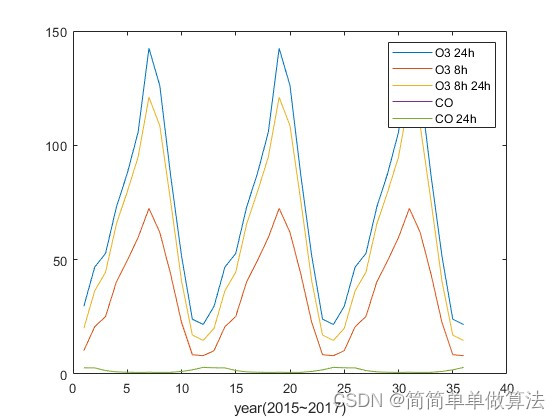
plot(data(11:15,:)');
legend('O3 24h','O3 8h','O3 8h 24h','CO','CO 24h');
xlabel('year(2015~2017)');
05_055m

4.算法理论概述

4.1 BP神经网络结构

        一个典型的BP（Backpropagation）神经网络包含输入层、隐藏层和输出层。假设我们有一个三层的BP神经网络，其结构如下：

  • 输入层：有n个节点，代表n种影响空气质量的因素（如PM2.5、SO2、NO2等）。
  • 隐藏层：有m个节点，每个节点表示一种潜在的非线性组合特征。
  • 输出层：有k个节点，对应k种空气质量指标预测值（如AQI指数）。

4.2 神经元模型与激活函数

对于第L层的第i个神经元，其输入信号为：

4.3 前向传播过程

       输入层至输出层的数据流动称为前向传播，对于空气质量预测问题，输入是历史空气质量数据和气象参数，经过多次非线性变换后，输出层得到预测的空气质量指数。

4.4反向传播算法及其误差函数

        训练神经网络的关键步骤是反向传播算法，用于更新网络中的权重和偏置以减小预测误差。首先定义一个损失函数（Cost Function）或误差函数，如均方误差(MSE)：

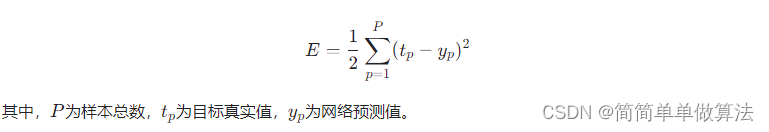
4.5 权重更新规则

        反向传播过程中，通过梯度下降法更新权重和偏置，以最小化误差函数。对于第l层的第i个神经元的权重wij(l)​，其更新规则为：

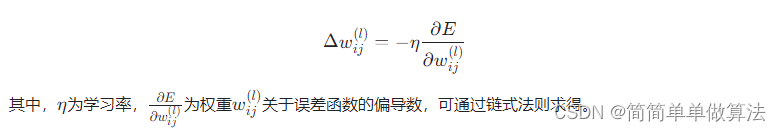
4.6 迭代训练

       重复以上步骤，对整个训练集进行多次迭代，直到达到预定的停止条件（如达到最大迭代次数或者误差满足阈值），最终得到训练好的BP神经网络模型，用于城市空气质量的预测。

       综上所述，BP神经网络通过对空气质量历史数据的学习，能够找出各因素与空气质量之间的内在规律，并通过优化权重矩阵实现对未来空气质量的预测。实际应用时还需考虑数据预处理、网络结构优化、超参数调整等问题，以提高预测的准确性和稳定性。

5.算法完整程序工程

OOOOO

OOO

O

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1544791.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Qt_day4:2024/3/25

Qt_day4:2024/3/25

作业1： 完善对话框，点击登录对话框，如果账号和密码匹配，则弹出信息对话框，给出提示”登录成功“，提供一个Ok按钮，用户点击Ok后，关闭登录界面，跳转到其他界面 如果账号和…
阅读更多...
一篇文章，告别Flutter状态管理争论，问题和解决

一篇文章，告别Flutter状态管理争论，问题和解决

起因 每隔一段时间，都会出现一个新的状态管理框架，最近在YouTube上也发现了有人在推signals, 一个起源于React的状态管理框架，人们总是乐此不疲的发明各种好用或者为了解决特定问题而产生的方案，比如Bloc, 工具会推陈出新&#x…
阅读更多...
qt table 简易封装，样式美化，以及 合并表格和颜色的区分 已解决

qt table 简易封装，样式美化，以及 合并表格和颜色的区分 已解决

在需求中&#xff0c; 难免会使用 table 进行渲染窗口&#xff0c;做一个简单的封装。美化表格最终效果&#xff01;&#xff01;&#xff01; 代码部分 // 显示 20行 20列CCendDetailsInfoTableWidget* table new CCendDetailsInfoTableWidget(20,10);for (int i 0; i < …
阅读更多...
ESCTF-逆向赛题WP

ESCTF-逆向赛题WP

ESCTF_reverse题解 逆吧腻吧babypybabypolyreeasy_rere1你是个好孩子完结撒花 Q_W_Q 逆吧腻吧 下载副本后无壳&#xff0c;直接拖入ida分析分析函数逻辑&#xff1a;ida打开如下&#xff1a;提取出全局变量res的数据后&#xff0c;编写异或脚本进行解密&#xff1a; a[0xBF, …
阅读更多...
enscan自动化主域名信息收集

enscan自动化主域名信息收集

enscan下载 Releases wgpsec/ENScan_GO (github.com) 能查的分类 实操&#xff1a; 首先打开linux 的虚拟机、 然后把下面这个粘贴到虚拟机中 解压后打开命令行 初始化 ./enscan-0.0.16-linux-amd64 -v 命令参数如下 oppo信息收集 运行下面代码时 先去配置文件把coo…
阅读更多...
JavaEE企业开发新技术3

JavaEE企业开发新技术3

目录 2.11 Method的基本操作-1 文字性概念描述 代码&#xff1a; 2.12 Method的基本操作-2 2.13 Method的基本操作-3 2.14 数组的反射操作-1 文字性概念&#xff1a; 代码&#xff1a; 2.15 数组的反射操作-2 学习内容 2.11 Method的基本操作-1 文字性概念描述 Me…
阅读更多...
io的学习4

io的学习4

打印流 分类&#xff1a;打印流一般是指&#xff1a;PrintStream、PrintWriter两个类 特点&#xff1a; 1.打印流只操作文件目的地&#xff0c;不操作数据源 2.特有的写出方法可以实现&#xff0c;数据原样写出 3.特有的写出方法&#xff0c;可以实现自动刷新&#xff0c;…
阅读更多...
仅用一个月，游卡完成从MySQL到上线OceanBase的实践

仅用一个月，游卡完成从MySQL到上线OceanBase的实践

编者按&#xff1a;自2023年9月起&#xff0c;游卡——国内最早卡牌游戏研发者之一&#xff0c;开始测试OceanBase&#xff0c;并在短短两个月内成功将三个核心业务应用迁移至OceanBase上。究竟是何因素促使游卡放弃游戏行业普遍采用的MySQL方案&#xff0c;转而大胆选择OceanB…
阅读更多...
荟萃分析R Meta-Analyses 3 Effect Sizes

荟萃分析R Meta-Analyses 3 Effect Sizes

总结 效应量是荟萃分析的基石。为了进行荟萃分析&#xff0c;我们至少需要估计效应大小及其标准误差。 效应大小的标准误差代表研究对效应估计的精确程度。荟萃分析以更高的精度和更高的权重给出效应量&#xff0c;因为它们可以更好地估计真实效应。 我们可以在荟萃分析中使用…
阅读更多...
一文整合工厂模式、模板模式、策略模式

一文整合工厂模式、模板模式、策略模式

为什么使用设计模式 今天终于有时间系统的整理一下这几个设计模式了&#xff0c; 这几个真是最常用的&#xff0c;用好了它们&#xff0c;你就在也不用一大堆的if else 了。能更好的处理大量的代码冗余问题。 在我们的实际开发中&#xff0c;肯定会有这样的场景&#xff1a;我…
阅读更多...
【C语言基础】：内存操作函数

【C语言基础】：内存操作函数

文章目录 一、memcpy函数的使用和模拟实现1.1 memcpy函数的使用1.2 memcpy函数的模拟实现 二、memmove函数的使用和模拟实现2.1 memmove函数的使用2.2 memmove函数的模拟实现 三、memset函数的使用3.1 menset函数的使用 四、memcmp函数的使用4.1 memcmp函数的使用 学海无涯苦作…
阅读更多...
Qt与编码

Qt与编码

ASCII码:一个字节&#xff0c;256个字符。 Unicode:字母&#xff0c;汉字都占用两个字节。 utf-8:字母一个字节&#xff0c;汉字3个字节。 gbk:字母一个字节&#xff0c;汉字2个字节。 gb2312:可以表示汉字&#xff0c;gb2312<gbk。 编码查看&#xff1a; https://www.…
阅读更多...
钡铼技术R40路由器助力构建无人值守的智能化污水处理厂

钡铼技术R40路由器助力构建无人值守的智能化污水处理厂

钡铼技术R40路由器作为智能化污水处理厂的关键网络设备&#xff0c;发挥着至关重要的作用&#xff0c;助力构建无人值守的智能化污水处理系统。在现代社会&#xff0c;污水处理是城市环境保护和可持续发展的重要组成部分&#xff0c;而智能化污水处理厂借助先进的技术和设备&am…
阅读更多...
C语言数据结构易错知识点（5）（插入排序、选择排序）

C语言数据结构易错知识点（5）（插入排序、选择排序）

插入排序&#xff1a;直接插入排序、希尔排序 选择排序&#xff1a;直接选择排序、堆排序 上述排序都是需要掌握的&#xff0c;但原理不会讲解&#xff0c;网上有很多详尽地解释&#xff0c;本文章主要分享一下代码实现上应当注意的事项 1.直接插入排序&#xff1a; 代码实…
阅读更多...
Kevin的128纪念日

Kevin的128纪念日

上面这个是我在三天前做的一个开场白一样的封面。在设计的时候我的想法很简单&#xff0c;把自己给展现出来。我没有去过多的加其他花花绿绿的东西&#xff0c;我想把我本身的状态和形象给凸显出来。 哈哈~看到这里有人就想问&#xff0c;这个躺在沙发上吃零食的懒猫就是你的个…
阅读更多...
利用瑞士军刀netcat建立连接并实现文件上传

利用瑞士军刀netcat建立连接并实现文件上传

实验环境&#xff1a; Kali:192.168.117.129 Windows10:192.168.135.142 第一步&#xff1a;建立连接 在Windows上下载netcat(官网搜索) 下载好之后在netcat目录打开cmd进入小黑屏 实验一&#xff1a;建立虚拟机与主机的连接 命令&#xff1a; Kali:nc 192.168.135.144…
阅读更多...
FastAPI+React全栈开发05 React前端框架概述

FastAPI+React全栈开发05 React前端框架概述

Chapter01 Web Development and the FARM Stack 05 The frontend React FastAPIReact全栈开发05 React前端框架概述 Let’s start with a bit of context here. Perhaps the changes in the world of the web are most visible when we talk about the frontend, the part o…
阅读更多...
前端学习之css基本网格布局

前端学习之css基本网格布局

网格布局 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>网格布局</title><style>.a{/* grid网格布局 */display: grid;width: 400px;height: 400px;border: 1px solid red;/* 设置当前…
阅读更多...
【Spring】IoCDI详解

【Spring】IoCDI详解

1. IoC详解 前面提到过IoC就是将对象的控制权交由Spring的IoC容器进行管理&#xff0c;由Spring的IoC容器创建和销毁bean&#xff0c;那么既然涉及到容器&#xff0c;就一定包含以下两方面功能&#xff1a; bean的存储bean的获取 1.1 类注解 Spring框架为了更好地服务应用程…
阅读更多...
RabbitMQ3.x之二_RabbitMQ所有端口说明及开启后台管理功能

RabbitMQ3.x之二_RabbitMQ所有端口说明及开启后台管理功能

RabbitMQ3.x之二_RabbitMQ所有端口说明及开启后台管理功能 文章目录 RabbitMQ3.x之二_RabbitMQ所有端口说明及开启后台管理功能1. RabbitMQ端口说明2. 开启Rabbitmq后台管理功能1. 查看rabbitmq已安装的插件2. 开启rabbitmq后台管理平台插件3. 开启插件后&#xff0c;再次查看插…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023