代码随想录算法训练营第二十九天|Leetcode332 重新安排行程、Leetcode51 N皇后、Leetcode37 解数独
- ● Leetcode332 重新安排行程
- ● 本题特点
- ● 解题思路
- ● 代码实现
- ● Leetcode51 N皇后
- ● 本题特点
- ● 解题思路
- ● 代码实现
- ● Leetcode37 解数独
- ● 本题特点
- ● 解题思路
- ● 代码实现
● Leetcode332 重新安排行程
题目链接:[Leetcode332 重新安排行程]
视频讲解:[代码随想录|重新安排行程]
题目描述:
● 本题特点
重新安排行程更像是深度优先搜索,但也是深度优先搜索中使用回溯,在查找路径的过程中需要用到回溯。
对于重新安排形成,我们需要注意:
(1)应该避免在处理航班形成的过程形成一个圈,成为死循环的情况;
(2)题目提示中如果存在多种有效的行程,请你按字符自然排序返回最小的行程组合。例如,行程 ["JFK", "LGA"] 与 ["JFK", "LGB"] 相比就更小,排序更靠前,字母序靠前应该排在前面,如何记录映射关系;
(3)使用确定回溯条件以及在搜索过程中,如何遍历一个机场对应的所有机场。
● 解题思路
(1)记录映射关系:
一个机场映射多个机场,机场之间靠字母字典序排列,可以使用std::unordered_map,如果多个机场之间有顺序则使用std::map/std::multimap/std::multiset。
将映射关系定义为:unordered_map<string, multimap<string, int>> targets,multimap<string, int>> targets表示unordered_map<出发机场, 到达机场的集合> targets,unordered_map<string, map<string, int>> targets表示unordered_map<出发机场, map<到达机场, 航班次数>> targets,这里不使用multiset是为了防止删除元素后迭代器失效;
(2)避免死循环:
使用unordered_map是为了方便我们在过程中增删元素,因为出发机场和到达机场是会重复的,搜索过程每及时删除目的机场就会导致死循环,在删除过程中可以使用航班次数这个子段做增减,标记到达机场是否使用过;
i.确定回溯函数的参数和返回值:
参数传入ticketNum表示有多少个航班,返回值使用bool,我们只需要找到一个形成,在树形结构中对应唯一的一条通向叶子节点的路线;
ii.确定回溯函数的终止条件:
由示例[[“MUC”, “LHR”], [“JFK”, “MUC”], [“SFO”, “SJC”], [“LHR”, “SFO”]] ,这是有4个航班,那么只要找出一种行程,行程里的机场个数是5就可以了,也就是回溯遍历过程中,如果达到了(航班数量+1),就找到了一个形成课可以把所有航班穿起来;
iii.确定回溯函数单层遍历逻辑:
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}
● 代码实现
class Solution {
private:
// unordered_map<出发机场, map<到达机场, 航班次数>> targets
unordered_map<string, map<string, int>> targets;
bool backtracking(int ticketNum, vector<string>& result) {
if (result.size() == ticketNum + 1) {
return true;
}
for (pair<const string, int>& target : targets[result[result.size() - 1]]) {
if (target.second > 0 ) { // 记录到达机场是否飞过了
result.push_back(target.first);
target.second--;
if (backtracking(ticketNum, result)) return true;
result.pop_back();
target.second++;
}
}
return false;
}
public:
vector<string> findItinerary(vector<vector<string>>& tickets) {
targets.clear();
vector<string> result;
for (const vector<string>& vec : tickets) {
targets[vec[0]][vec[1]]++; // 记录映射关系
}
result.push_back("JFK"); // 起始机场
backtracking(tickets.size(), result);
return result;
}
};
● Leetcode51 N皇后
题目链接:Leetcode51 N皇后
视频讲解:代码随想录|N皇后
题目描述:按照国际象棋的规则,皇后可以攻击与之处在同一行或同一列或同一斜线上的棋子。
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。
每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。
示例 1:
输入:n = 4
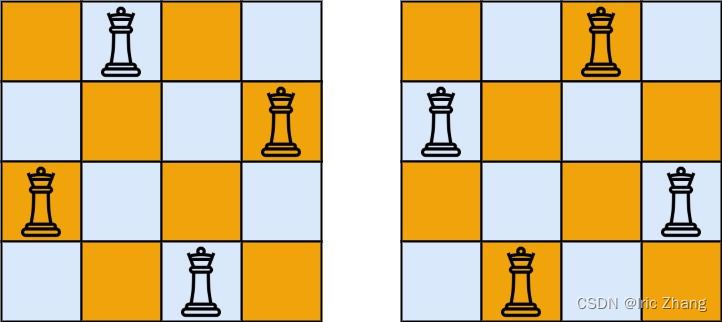
输出:[[“.Q…”,“…Q”,“Q…”,“…Q.”],[“…Q.”,“Q…”,“…Q”,“.Q…”]]
解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1
输出:[[“Q”]]
提示:
1 <= n <= 9
● 本题特点
对于N皇后的解决同样可以构造成递归过程的树形结构,只不过不同于之前组合、分割、子集、子序列问题,在每一个结点都是一个chessboard结构,我们在chessboard中填入皇后Q,并使其满足同行、同列以及45°、135°位置不存在任何皇后,保证chessboard上皇后们的和谐;树的深度取决于chessboard的规模。
● 解题思路
首先我们需要解决N皇后在空格填入皇后的检验,也就是检验棋盘是否合法:
(1)不能同行:
因为在单层搜索的过程中,每一层递归,只会选for循环里的一个元素,所以对于行而言不需要做检验操作;
(2)不能同列:
检查同列上是否存在皇后,该过程我们传入的列col是不变了,需要循环遍历行row检查是否有chessboard[i][col] == Q是否满足;
for (int i = 0; i < row; i++) { // 这是一个剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
(3)不能同斜线:
同斜线包括两部分:45°和135°。
45°在第一象限,因此我们需要检测的是[row - 1, col + 1]向右上方延申的格子是否有皇后;
for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
135°在第二象限,因此我们需要检测的是[row - 1, col - 1]向左上方延申的各自是否有皇后;
for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
i.确定回溯函数的参数和返回值:
定义全局二维数组result记录最终结果,参数n是chessboard的大小,row记录当前遍历第几层;
ii.确定回溯函数的终止条件:
当遍历到最后一行时,即row == n时,遍历结束;
iii.确定回溯函数单层遍历逻辑:
递归深度就是row控制棋盘的行,每一层里for循环的col控制棋盘的列,一行一列,确定了放置皇后的位置。
● 代码实现
class Solution {
private:
vector<vector<string>> result;
void backtracking(vector<string>& chessboard, int n, int row)
{
if(row == n)
{
result.push_back(chessboard);
return;
}
for(int col = 0; col < n; col++)
{
if(isValid(chessboard, n, row, col))
{
chessboard[row][col] = 'Q';
backtracking(chessboard, n, row + 1);
chessboard[row][col] = '.';
}
}
}
bool isValid(vector<string>& chessboard, int n, int row, int col)
{
//同列检查
for(int i = 0; i < row; i++)
{
if(chessboard[i][col] == 'Q')
{
return false;
}
}
//45°检查
for(int i = row - 1, j = col + 1; i >= 0 && j < n; --i, ++j)
{
if(chessboard[i][j] == 'Q')
{
return false;
}
}
//135°检查
for(int i = row - 1, j = col - 1; i >= 0 && j >= 0; --i, --j)
{
if(chessboard[i][j] == 'Q')
{
return false;
}
}
return true;
}
public:
vector<vector<string>> solveNQueens(int n) {
vector<string> chessboard(n, string(n, '.'));
backtracking(chessboard, n, 0);
return result;
}
};
● Leetcode37 解数独
题目链接:Leetcode37 解数独
视频讲解:代码随想录|解数独
题目描述:编写一个程序,通过填充空格来解决数独问题。
数独的解法需 遵循如下规则:
数字 1-9 在每一行只能出现一次。
数字 1-9 在每一列只能出现一次。
数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。(请参考示例图)
数独部分空格内已填入了数字,空白格用 ‘.’ 表示。
示例 1:
输入:board = [[“5”,“3”,“.”,“.”,“7”,“.”,“.”,“.”,“.”],[“6”,“.”,“.”,“1”,“9”,“5”,“.”,“.”,“.”],[“.”,“9”,“8”,“.”,“.”,“.”,“.”,“6”,“.”],[“8”,“.”,“.”,“.”,“6”,“.”,“.”,“.”,“3”],[“4”,“.”,“.”,“8”,“.”,“3”,“.”,“.”,“1”],[“7”,“.”,“.”,“.”,“2”,“.”,“.”,“.”,“6”],[“.”,“6”,“.”,“.”,“.”,“.”,“2”,“8”,“.”],[“.”,“.”,“.”,“4”,“1”,“9”,“.”,“.”,“5”],[“.”,“.”,“.”,“.”,“8”,“.”,“.”,“7”,“9”]]
输出:[[“5”,“3”,“4”,“6”,“7”,“8”,“9”,“1”,“2”],[“6”,“7”,“2”,“1”,“9”,“5”,“3”,“4”,“8”],[“1”,“9”,“8”,“3”,“4”,“2”,“5”,“6”,“7”],[“8”,“5”,“9”,“7”,“6”,“1”,“4”,“2”,“3”],[“4”,“2”,“6”,“8”,“5”,“3”,“7”,“9”,“1”],[“7”,“1”,“3”,“9”,“2”,“4”,“8”,“5”,“6”],[“9”,“6”,“1”,“5”,“3”,“7”,“2”,“8”,“4”],[“2”,“8”,“7”,“4”,“1”,“9”,“6”,“3”,“5”],[“3”,“4”,“5”,“2”,“8”,“6”,“1”,“7”,“9”]]
解释:输入的数独如上图所示,唯一有效的解决方案如下所示:
提示:
board.length == 9
board[i].length == 9
board[i][j] 是一位数字或者 ‘.’
题目数据 保证 输入数独仅有一个解
● 本题特点
不同于N皇后的问题,数独问题的解决需要使用二维递归,一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性不仅需要判断行是否满足条件,还需要列也满足条件,本题每一个位置都需要放入一个数字,并检查数字摆放的合法性,因此解数独的树形结构比N皇后更宽更深。
● 解题思路
i.确定回溯函数的参数和返回值:
本题回溯函数返回值为bool类型,因为解数独找到一个符合条件就立刻返回,相当于找从根结点到叶子结点的一条唯一路径;
ii.确定回溯函数的终止条件:
当遍历到最后一行一列的时候,也就是将数独填写完成,循环自动退出,回溯函数也自然退出
iii.确定回溯函数单层遍历逻辑:
一个for循环遍历棋盘的行,一个for循环遍历棋盘的列,一行一列确定下来之后,递归遍历这个位置放9个数字的可能性。
注意这里return false的地方:因为如果一行一列确定下来了,这里尝试了9个数都不行,说明这个棋盘找不到解决数独问题的解;那么会直接返回, 这也就是为什么没有终止条件也不会永远填不满棋盘而无限递归下去。
bool backtracking(vector<vector<char>>& board) {
for (int i = 0; i < board.size(); i++) { // 遍历行
for (int j = 0; j < board[0].size(); j++) { // 遍历列
if (board[i][j] != '.') continue;
for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
if (isValid(i, j, k, board)) {
board[i][j] = k; // 放置k
if (backtracking(board)) return true; // 如果找到合适一组立刻返回
board[i][j] = '.'; // 回溯,撤销k
}
}
return false; // 9个数都试完了,都不行,那么就返回false
}
}
return true; // 遍历完没有返回false,说明找到了合适棋盘位置了
}
● 代码实现
class Solution {
private:
bool backtracking(vector<vector<char>>& board)
{
for(int i = 0; i < board.size(); i++)
{
for(int j = 0; j < board[0].size(); j++)
{
if(board[i][j] == '.')
{
for(char k = '1'; k <= '9'; k++)
{
if(isValid(board, i, j, k))
{
board[i][j] = k;
if(backtracking(board)) return true;
board[i][j] = '.';
}
}
return false;
}
}
}
return true;
}
bool isValid(vector<vector<char>>& board, int row, int col, char k)
{
//检查行
for(int i = 0; i < 9; i++)
{
if(board[row][i] == k)
{
return false;
}
}
//检查列
for(int j = 0; j < 9; j++)
{
if(board[j][col] == k)
{
return false;
}
}
//检查九宫格
int startRow = (row / 3) * 3;
int startCol = (col / 3) * 3;
for(int i = startRow; i < startRow + 3; ++i)
{
for(int j = startCol; j < startCol + 3; ++j)
{
if(board[i][j] == k)
{
return false;
}
}
}
return true;
}
public:
void solveSudoku(vector<vector<char>>& board) {
backtracking(board);
}
};



![LeetCode每日一题[c++]-322.零钱兑换](https://img-blog.csdnimg.cn/direct/ac538a8588c3496eae163cacb0d1863e.png)