文献阅读笔记(Transformer)
- 摘要
- Abstract
- 1、文献阅读
- 1.1 文献题目
- 1.2 文献摘要
- 1.3 研究背景
- 1.4 模型架构
- 1.4.1 Encoder-Decoder
- 1.4.2 注意力机制
- 1.4.3 多头注意力
- 1.4.4 Position-wise Feed-Forward Networks
- 1.4.5 Embeddings and Softmax
- 1.4.6 Positional Encoding
- 2. Transformer公式推导以及原理
- 3. Transformer整体执行流程
- 3.1 masked self-attention推导以及原理细节
- 总结
摘要
Transformer是一种流行的神经网络架构,用于处理自然语言处理(NLP)任务。它由"Attention is All You Need"一文中提出,相对于传统的循环神经网络(RNN)模型,Transformer采用了自注意力机制(self-attention),使得模型能够更好地捕捉输入序列中各个位置之间的关系。它通过同时考虑输入序列中的所有位置信息,而无需像RNN那样逐个位置地进行处理,大大提高了训练和推理的效率。Transformer的成功部分得益于其并行计算的能力和深层网络的表示能力。这使得Transformer模型能够处理长文本序列,同时提供更好的建模能力和上下文理解能力。本文将详细介绍Transformer的具体执行流程和原理。
Abstract
Transformer is a popular neural network architecture for natural language processing (NLP) tasks. Proposed in the article “Attention is All You Need”, Transformer employs a self-attention mechanism that allows the model to better capture the relationships between the positions in the input sequence, as opposed to the traditional recurrent neural network (RNN) model. It greatly improves the efficiency of training and inference by considering all the positional information in the input sequence at the same time, without having to process it position-by-position as in an RNN.Transformer’s success is due in part to its ability to parallelize the computation and representation of the deep network. This allows the Transformer model to process long text sequences while providing better modeling capabilities and contextual understanding. In this paper, we describe in detail the specific implementation process and principles of Transformer.
1、文献阅读
1.1 文献题目
题目:Attention Is All You Need
文献链接:https://arxiv.org/abs/1706.03762
1.2 文献摘要
主导序列转录模型基于复杂的循环或卷积神经网络,包括编码器和解码器。性能最好的模型还通过注意力机制连接编码器和解码器。文章主要提出了一种称为 Transformer 的新型网络架构,它完全基于注意力机制,完全不需要递归和卷积。对两个机器翻译任务的实验表明,这些模型具有卓越的质量,同时具有更高的并行性,并且需要的训练时间显着减少。
remark
所谓序列转录模型通俗理解就是给机器一个序列,机器生成另外一个序列
Dominant sequence transduction models are based on complex recurrent or convolutional neural networks, including encoders and decoders. The best performing models also connect the encoder and decoder through an attention mechanism. The article focuses on proposing a novel network architecture called Transformer, which is based entirely on the attention mechanism and does not require recursion and convolution at all. Experiments on two machine translation tasks show that these models have superior quality along with higher parallelism and require significantly less training time.
1.3 研究背景
减少顺序计算的目标也构成了扩展神经 GPU 、ByteNet 和 ConvS2S 的基础,这些模型都以卷积神经网络为基本构件,并行计算所有输入和输出位置的隐藏表示。在这些模型中,关联来自两个任意输入或输出位置的信号所需的操作数量随着位置之间的距离而增加,这使得学习遥远位置之间的依赖关系变得更加困难。在 Transformer 中,凭借其强大的自注意力机制和多头注意力机制,可以将其操作数降低至恒定数量。本文献提出的Transformer架构 是第一个完全依赖自注意力来计算其输入和输出表示的转换模型。
1.4 模型架构
大多数序列转导模型都具有 encoder-decoder 结构,Transformer模型中的编码器将符号表示的输入序列(
x
1
、
x
2
、
x
3
、
.
.
.
、
x
n
x_1、x_2、x_3、... 、x_n
x1、x2、x3、...、xn)映射到连续表示的序列
z
=
(
z
1
、
z
2
、
.
.
.
、
z
n
)
z=(z_1、z_2、... 、z_n)
z=(z1、z2、...、zn),给定
z
z
z,解码器然后每次生成一个元素的符号输出序列 (
y
1
,
.
.
.
,
y
m
y_1, ..., y_m
y1,...,ym)。在每个步骤中,模型都是自回归的,在生成下一个时将先前生成的符号用作附加输入,即模型会在生成序列时考虑到上下文信息,并根据已经生成的部分来决定下一个要生成的元素,也可以理解为过去时刻
t
−
1
t-1
t−1 的输出都会作为当前时刻
t
t
t 的输入。如下Transformer结构图:

1.4.1 Encoder-Decoder
编码器(Encoder)
编码器由 N = 6 N = 6 N=6 个相同层的堆栈组成。每层有两个子层。第一层是多头自注意力机制,第二层是简单的位置全连接前馈网络。作者在两个子层周围采用残差连接,然后对其进行层归一化。即每个子层的输出为 L a y e r N o r m ( x + S u b l a y e r ( x ) ) LayerNorm(x + Sublayer(x)) LayerNorm(x+Sublayer(x)),其中 S u b l a y e r ( x ) Sublayer(x) Sublayer(x) 是子层本身实现的函数。6个子层分别是:
- Self-Attention(自注意力)层:该层使用自注意力机制来计算输入序列中每个位置的表示,并捕捉输入序列内部的依赖关系。
- Multi-Head Attention(多头注意力)层:该层在自注意力的基础上使用多个头(可以理解为子注意力)来同时计算不同的注意力表示,从而捕捉更丰富的信息。
- Feed-Forward(前馈)层:该层使用全连接神经网络来对每个位置的表示进行非线性变换。
- 残差连接(Residual Connection):在每个子层结束时,将其输入和输出通过残差连接进行相加,以便信息可以更加顺利地传递和保持梯度流。
- 层归一化(Layer Normalization):在残差连接之后,对输出向量进行层归一化操作,以加速训练过程和提升模型的鲁棒性。
- 位置编码(Positional Encoding):前馈层和自注意力层都采用了位置编码(Positional Encoding)来为输入序列的每个位置添加位置信息,从而帮助模型理解输入序列中元素的位置关系。
remark
通俗理解,编码器的作用是生成序列中每个词的注意力信息
解码器(Decoder)
解码器也是由N=6个相同层的堆栈组成。除了每个编码器层中的两个子层之外,解码器还插入第三个子层,该子层对编码器堆栈的输出执行多头注意力。与编码器类似,作者在每个子层周围采用残差连接,然后进行层归一化。作者修改了解码器堆栈中的自注意力子层,以防止位置关注后续位置。这种掩蔽与输出嵌入偏移一个位置的事实相结合,确保位置 i 的预测只能依赖于小于 i 的位置处的已知输出。
remark
解码器的作用是生成文本序列,解码器最开始的输入是由编码器的输出以及解码器输入的起始符start组成,当解码器以一个结束符end输出时,则表明文本序列生成完成。如下图:

1.4.2 注意力机制
注意力函数可以描述为将一个查询和一组键值对映射到一个输出,其中查询Q、键K、值V和输出都是向量。输出是以值V的加权和来计算的,其中分配给每个值V的权重是通过查询Q与相应键K的兼容函数来计算的。

Scaled Dot-Product Attention
缩放点积的输入包括查询Q和键K的维度 d k d_{k} dk以及值得维度 d v d_{v} dv。计算查询Q和键K得点积,然后将每个结果除以 d k \sqrt{d_k} dk,用 sfotmax() 函数来获得值得权重 。
在实践中,我们同时计算一组查询的注意力函数,将其打包到矩阵 Q 中。键和值也打包到矩阵 K 和 V 中。我们将输出矩阵计算为: A t t e n t i o n ( Q , K , V ) = s o f t m a x ( Q K T d k ) Attention(Q,K,V)=softmax(\frac{QK^{T}}{\sqrt{d_{k}}} ) Attention(Q,K,V)=softmax(dkQKT)常用的有两种注意力机制,加法质注意力 和 点积(乘性质)注意力。点积注意力和本文的注意力相同,除了使用缩放因子 1 d k \frac{1}{\sqrt{d_{k}}} dk1。加法注意力使用具有单个隐藏层的前馈网络计算兼容性函数。 虽然两者在理论复杂度上相似,但点积注意力在实践中速度更快,空间效率更高,因为它可以使用高度优化的矩阵乘法代码来实现。
虽然对于较小的 d k d_k dk值,这两种机制的表现相似,但加性注意力优于点积注意力,而无需针对较大的 d k d_{k} dk 值进行缩放。我们怀疑对于较大的 d k d_{k} dk 值,点积的量级会变大,从而将 s o f t m a x softmax softmax 函数推入梯度极小的区域。为了抵消这种影响,我们将点积缩放 1 d k \frac{1}{\sqrt{d_{k}}} dk1。
remark
注意力的计算机指是,对每个 Q 和 K做内积,将它作为相似度。当两个向量做内积时,如果他俩的 d 相同,向量内积越大,余弦值越大,相似度越高。如果内积值为0,他们是正交的,相似度也为0。
1.4.3 多头注意力
在该文章中,作者通过添加一种多头注意力机制,进一步完善了自注意力层。具体做法:首先,通过 h 个不同的线性变换对 Query、Key 和 Value 进行映射;然后,将不同的 Attention 拼接起来;最后,再进行一次线性变换。每一组注意力用于将输入映射到不同的子表示空间,这使得模型可以在不同子表示空间中关注不同的位置。整个计算过程可表示为:

多头注意力机制与卷积神经网络有些相似,卷积神经网络中,我们往往希望能够提取到的特征越多越好,而在文本中,我们也希望能够得到的特征越多越好。我们一组Q、K、V矩阵,得到一组特征表达,那么我们多组Q、K、V,就会得到多组特征表达。就比如第一个词,根据上述的计算过程,我们一开始有一组
Q
1
、
K
1
、
V
1
Q_1、K_1、V_1
Q1、K1、V1矩阵,能够得到最后特征表达的值
Z
1
Z_1
Z1,如果再来一组
Q
2
、
K
2
、
V
2
Q_2、K_2、V_2
Q2、K2、V2,那么最后会得到另一组特征表达的值
Z
2
Z_2
Z2,以此类推。通过不同的head得到多个特征表达,通俗来讲,就是通过多组的
Q
、
K
、
V
Q、K、V
Q、K、V,最终得到多个
Z
i
Z_i
Zi 的值。一般情况下,所谓的多头机制,基本上都是只有8个head。然后通过8组head得到8个特征表达,最终将8个特征拼接在一起,通过全连接层进行降维,最后得到的一个特征可能会比之前用一组head得到的特征表现更好。
remark
通俗来说,多头注意力机制就是将原来的一组
Q
、
K
、
V
Q、K、V
Q、K、V增加至八组,就类似于CNN的多层卷积一样,卷积层越多,提取的特征越好。而多头注意力机制也同理。
F
F
N
(
x
)
=
m
a
x
(
0
,
x
W
1
+
b
1
)
W
2
+
b
2
FFN(x)=max(0,xW_{1}+b_{1})W_{2}+b_{2}
FFN(x)=max(0,xW1+b1)W2+b2虽然不同位置的线性变换是相同的,但它们在层与层之间使用不同的参数。
1.4.4 Position-wise Feed-Forward Networks
除了注意力子层之外,我们的编码器和解码器中的每一层都包含一个完全连接的前馈网络,该网络分别且相同地应用于每个位置。 这由两个线性变换组成,中间有一个 ReLU 激活。
1.4.5 Embeddings and Softmax
由于输入的为词,我们需要将其映射为向量,通俗来说,embedding就是给任何一个词,用一个长为 d m o d e l d_{model} dmodel的向量来表示它,在该文献中, d m o d e l = 512 d_{model}=512 dmodel=512,即编码器和解码器都需要有Embedding,在进入Softmax的输入端也需要进行Embedding。
1.4.6 Positional Encoding
简单理解就是需要给每个词向量加上位置编码,用以联系上下文,即这些词向量不管排列顺序如何发生变化,最终通过attention后,输出的注意力分数仍然不变,因为attention没有时序信息。
2. Transformer公式推导以及原理
RNN模型是分阶段执行的,即第一个时间段执行完后,才开始执行下一个时间点,整体执行过程为串行,输入序列需要一个个输入进模型中,输出序列也是一个个输出,这样的效率和性能较低。而Transformer拥有其强大的完全自注意力机制,能够实现序列处理的并行化,即输入一排向量,输出一排向量。
下面,我们来具体看一下Attention机制的推导过程以及每个词的注意力分数是如何计算的:
我们首先输入四个词向量
x
1
、
x
2
、
x
3
、
x
4
x^1、x^2、x^3、x^4
x1、x2、x3、x4,它们各自会分别乘上
W
q
、
W
k
、
W
v
W_q、W_k、W_v
Wq、Wk、Wv,生成新向量
q
(
q
u
e
r
y
)
、
k
(
k
e
y
)
、
v
(
v
a
l
u
e
)
q(query)、k(key)、v(value)
q(query)、k(key)、v(value),这里的
W
q
、
W
k
、
W
v
W_q、W_k、W_v
Wq、Wk、Wv为四个词向量共享的参数,计算公式如下
q
i
=
W
q
x
i
q^{i}=W_{q}x^{i}
qi=Wqxi
k
i
=
W
k
x
i
k^{i}=W_{k}x^{i}
ki=Wkxi
v
i
=
W
v
x
i
v^{i}=W_{v}x^{i}
vi=Wvxi我们以输出第一个向量
y
1
y^{1}
y1为例,来了解一下attention机制的全部流程:
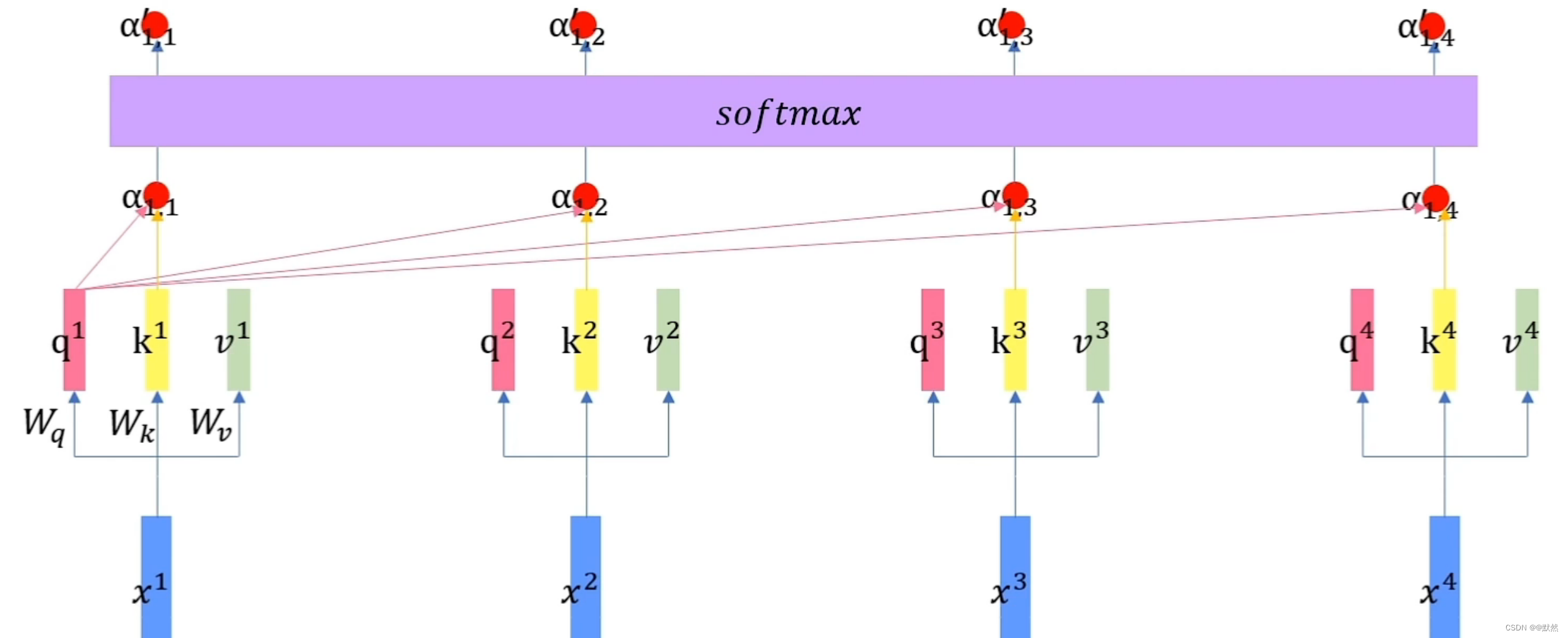
- 首先向量 q 1 q^{1} q1会和每个词向量对应的的 k k k 向量作内积,在本例中, q 1 q^{1} q1 和 k 1 k^{1} k1 内积得到 α 1 , 1 \alpha_{1,1} α1,1, q 1 q^{1} q1 和 k 2 k^{2} k2 内积得到 α 1 , 2 \alpha_{1,2} α1,2, q 1 q^{1} q1 和 k 3 k^{3} k3 内积得到 α 1 , 3 \alpha_{1,3} α1,3, q 1 q^{1} q1 和 k 4 k^{4} k4 内积得到 α 1 , 4 \alpha_{1,4} α1,4,在这里, α \alpha α代表的是每个词的注意力分数,该值越大,就说明这个位置更重要一些。
- 然后所有的
α
\alpha
α 注意力分数会通过一个softmax层,得到
α
′
\alpha^{'}
α′,分别为
α
1
i
′
,
i
=
1
,
2
,
3
,
4
\alpha^{'}_{1i},i=1,2,3,4
α1i′,i=1,2,3,4,如下图所示:
- 然后我们将得到的
α
′
\alpha^{'}
α′与其对应词向量的
v
v
v 相乘,让
α
1
,
1
′
\alpha^{'}_{1,1}
α1,1′乘上
v
1
v^{1}
v1、
α
1
,
2
′
\alpha^{'}_{1,2}
α1,2′乘上
v
2
v^{2}
v2、
α
1
,
3
′
\alpha^{'}_{1,3}
α1,3′乘上
v
3
v^{3}
v3、
α
1
,
4
′
\alpha^{'}_{1,4}
α1,4′乘上
v
4
v^{4}
v4,将所有的乘积结果相加起来,得到最终的输出
y
1
y^{1}
y1,如下图所示:
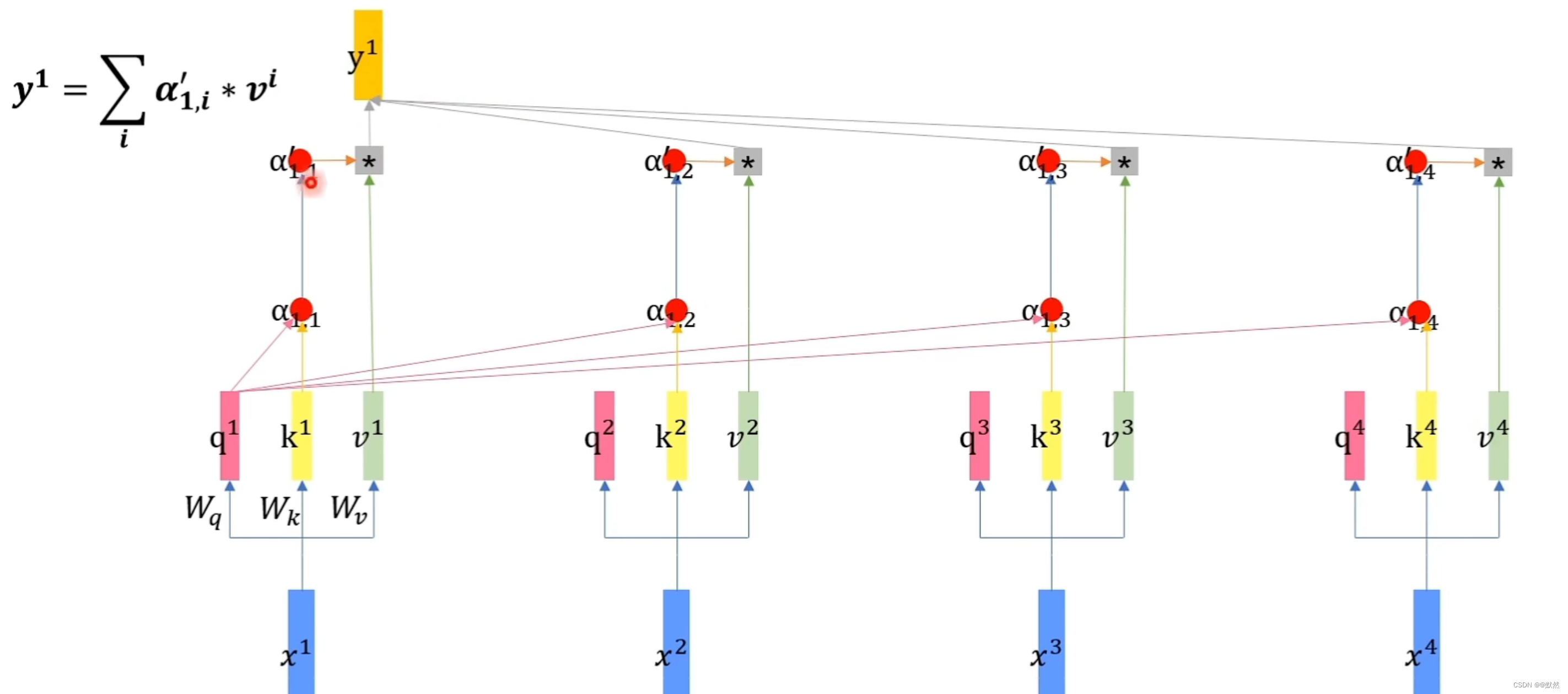
我们可以发现 α ′ \alpha^{'} α′ 相当于是向量 v v v 的权重,假设 α 1 , 2 ′ \alpha^{'}_{1,2} α1,2′的值很大,那么我们在做按权求和的时候, v 2 v^{2} v2就会有更多的信息传入到 y 1 y^{1} y1,即 v 2 v^{2} v2得到了更多的关注。
下面我们用矩阵变换的思维回顾下这一整个过程:
首先是
x
x
x 向量分别乘上
W
q
、
W
k
、
W
v
W_q、W_k、W_v
Wq、Wk、Wv,生成
q
、
k
、
v
q、k、v
q、k、v 向量,这里,我们以生成
q
2
q_2
q2 向量为例,假设目标
q
2
q_2
q2的维度为2,输入向量
x
2
x_2
x2的维度为3,那么我们就需要训练一个2*3的矩阵进行转换,这里的
W
q
W_q
Wq 为两行三列,
x
2
x^2
x2为三行一列,这里实现了
x
2
x^2
x2 到
q
2
q^2
q2 的转换,同理,可以依次得到
q
1
、
q
3
、
q
4
q^1、q^3、q^4
q1、q3、q4,如下图:

然后我们将向量拼接成一个矩阵,同理,按照这种方式,可以得到
K
、
V
K、V
K、V矩阵


接下来分别让
q
2
q^2
q2与
k
1
、
k
2
、
k
3
、
k
4
k^1、k^{2}、k^3、k^4
k1、k2、k3、k4做内积,分别得到
α
2
,
1
、
α
2
,
2
、
α
2
,
3
、
α
2
,
4
\alpha_{2,1}、\alpha_{2,2}、\alpha_{2,3}、\alpha_{2,4}
α2,1、α2,2、α2,3、α2,4,这里得到的
α
2
,
1
、
α
2
,
2
、
α
2
,
3
、
α
2
,
4
\alpha_{2,1}、\alpha_{2,2}、\alpha_{2,3}、\alpha_{2,4}
α2,1、α2,2、α2,3、α2,4均是 1 * 1 的向量,由于
q
2
q^2
q2为 2 * 1 的向量,
k
1
k^1
k1 为 2 * 1 的向量,此时我们需要将
k
k
k 进行转置,将其转换成 1 * 2 的向量,最终得到的
α
2
,
i
\alpha_{2,i}
α2,i 均为 1 * 1 的向量,我们可以将这四次矩阵运算整合成一次,将转置后的每个词向量的
k
k
k 上下堆叠,因此最终得到一个 4 * 1 的
α
\alpha
α 向量。
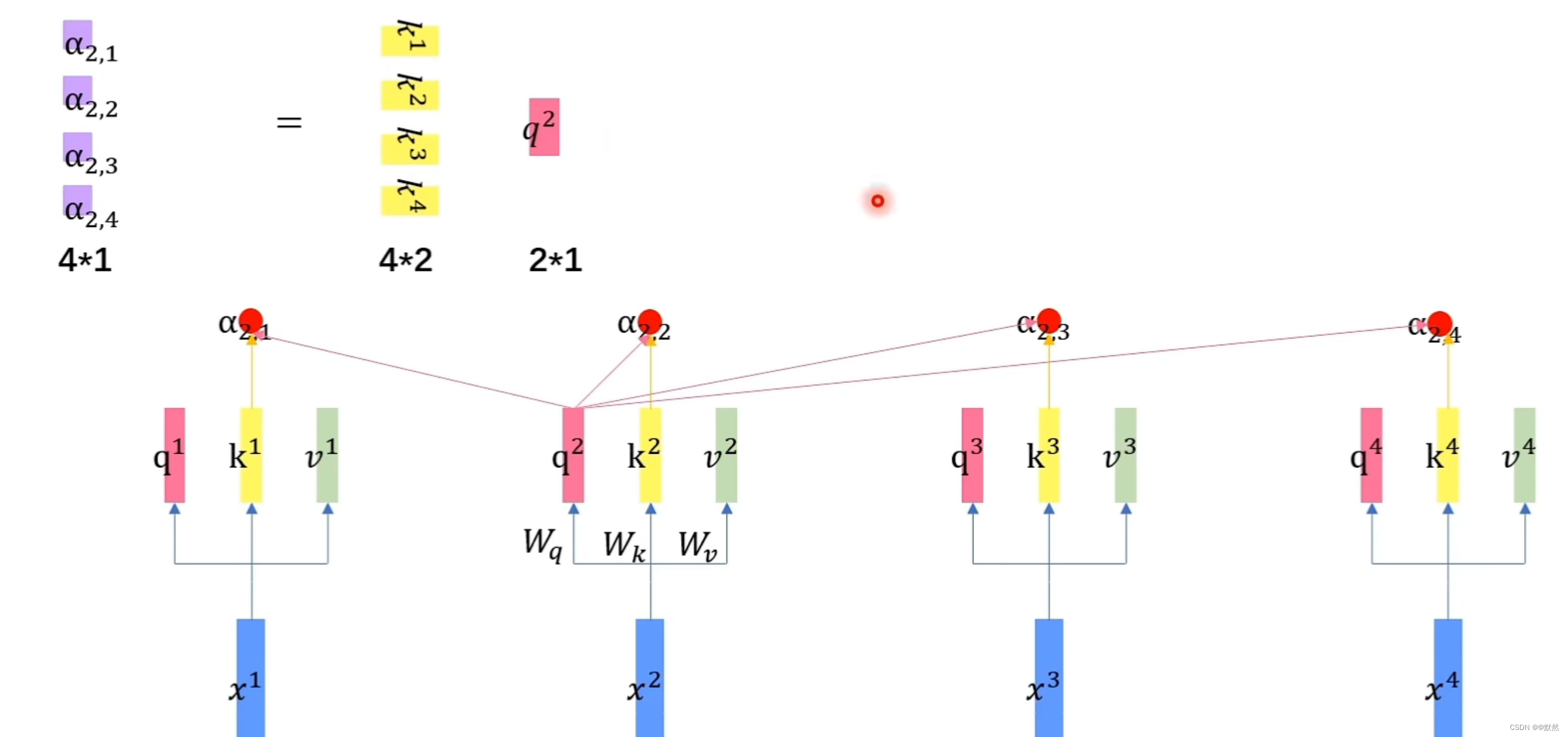
同理可以计算出其他词向量的注意力得分,将
α
\alpha
α 矩阵记为
A
A
A,将堆叠的
k
k
k 记为
K
T
K^{T}
KT,将
q
q
q 记为
Q
Q
Q,
A
=
K
T
Q
A=K^{T}Q
A=KTQ

然后将每一列的
α
\alpha
α 做一次 softmax 的操作,进行归一化,即
A
′
=
s
o
f
t
m
a
x
(
A
)
A^{'}=softmax(A)
A′=softmax(A)

最终我们将所有的
α
2
,
i
\alpha_{2,i}
α2,i乘上
v
i
v^i
vi,然后将其相加,得到
y
2
=
α
2
,
1
v
1
+
α
2
,
2
v
2
+
α
2
,
3
v
3
+
α
2
,
4
v
4
y^{2}=\alpha_{2,1}v^{1}+\alpha_{2,2}v^{2}+\alpha_{2,3}v^{3}+\alpha_{2,4}v^{4}
y2=α2,1v1+α2,2v2+α2,3v3+α2,4v4,按照此思路,我们可以计算出其他词向量的输出值。
从上述推导过程中,我们可以发现,attention机制是忽视序列长度的,无论两个输入向量相隔有多远,q与k做内积,就能知道当前的词需要放多少注意力在序列中的各个词上,做到了通过语境、语意同步,联系了上下文。在处理序列任务的attention模型中,常常会对输入的词向量进行位置编码,对不同位置的词向量,加上不同的位置向量
3. Transformer整体执行流程
Transformer模型整体分为编码器和解码器,编码器用于提取输入的信息,比如我们用一排one-hot编码的向量作为编码器的输入,编码器就会自动的帮我们提取这句序列文本中有用的信息,得到另外一排向量,然后解码器结合编码器提取的信息来预测输出的结果,在解码器这部分就涉及到了transformer的另外一个特性——自回归,所谓自回归,就是前一时间段的输出会作为下一时间段的输入。
我们往解码器里输入一串向量,< bos > 代表 beginning of the sentence,表示形式为one-hot,然后解码器会根据编码器的输出和向量< bos >的信息输出第一个预测结果,然后再结合上一时间段解码器的输出结果和编码器的输出,输出第二个预测结果,以此类推,直至解码器输出终止向量< eos >代表endding of the sentence,当模型解码器发现已经输出了 < eos > 向量,也就是代表了整个序列文本已经输出完毕,因此也就可以停止运行,这就是自回归。

接下来我们来模拟下transformer编码器:
我们输入一排向量 nerver say never,首先会经过一个 input embedding 层,这样我们的词就会变成了词向量,接着就和上文我们所学习的attention模型一样,对每个向量进行位置编码,得到一排新的输出。

然后经过一个 self-attention 层,第一个向量生成的 q 与 所有的 k 作内积,得到
α
\alpha
α,接着
α
\alpha
α 做一个softmax操作,得到
α
′
\alpha^{'}
α′,所有的
v
v
v 乘上每个词向量对应的
α
′
\alpha^{'}
α′,然相加,得到最终的输出
y
1
y^{1}
y1, 同理,我们可以得到
y
2
、
y
3
、
y
4
y^{2}、y^{3}、y^{4}
y2、y3、y4,在编码器中,输入多少向量,输出就会有多少向量。

然后要经过一个 add&norm 层,它要对输入的向量进行残差连接和 layer normalization层标准化的操作,残差连接就是做做一个相加的操作,将原来的输入向量与selft-attention输出的向量相加,得到新的一排向量,在这里两组向量相加,需要保证两组向量的维度相同,残差连接目的是使得信息能够在网络中能够更好的传递,并帮助减轻梯度消失的问题。
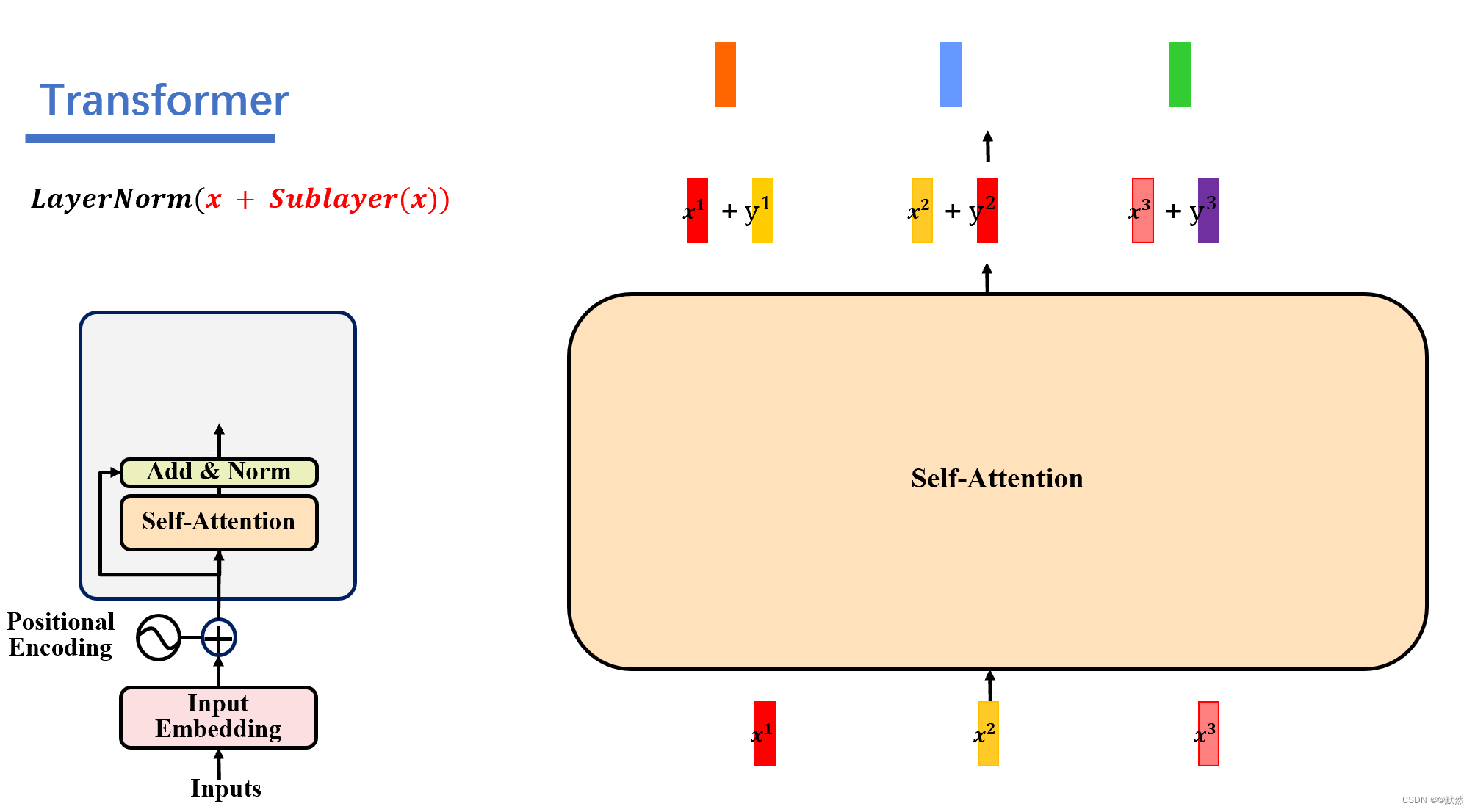
这里的层标准化指的就是每个输出向量各自做一个标准化,即所有特征减去一个均值,除上标准差。就比如通过残差连接后,其中一个输出向量为
[
1
3
5
]
\begin{bmatrix}1\\3\\5\end{bmatrix}
⎣⎡135⎦⎤,均值
μ
=
1
+
3
+
5
3
=
3
\mu=\frac{1+3+5}{3}=3
μ=31+3+5=3,标准差
σ
=
(
1
−
3
)
2
+
(
3
−
3
)
2
+
(
5
−
3
)
2
3
≈
1.63
\sigma=\sqrt{\frac{(1-3)^2+(3-3)^2+(5-3)^2}{3} }\approx1.63
σ=3(1−3)2+(3−3)2+(5−3)2≈1.63,因此
[
(
1
−
3
)
2
1.63
(
3
−
3
)
2
1.63
(
5
−
3
)
2
1.63
]
=
[
−
1.83
0
1.83
]
\begin{bmatrix}\frac{(1-3)^2}{1.63}\\\frac{(3-3)^2}{1.63}\\ \frac{(5-3)^2}{1.63}\end{bmatrix}=\begin{bmatrix}-1.83\\0\\1.83\end{bmatrix}
⎣⎢⎡1.63(1−3)21.63(3−3)21.63(5−3)2⎦⎥⎤=⎣⎡−1.8301.83⎦⎤,得到的就是标准化后的向量,同理,残差连接后的所有向量都要做一个layer normalization的操作。然后所有的向量都会经过一个 feed forward 层,它本质上就是一个全连接网络,然后得到一排相同维度和数量的向量,再进行残差连接和层标准化操作,这样我们的编码器部分就结束了。

接下来就是解码器部分,解码器这部分除了需要接受编码器的输入信息外,它还是自回归的,同编码器一样,我们需要对解码器的输入做一个output embedding操作,这里output embedding是逐个时间步对序列模型输出进行嵌入的过程,而不是一次性对所有序列进行嵌入,具体通过根据编码器输出向量的数量和维度,首先随机生成其对应数量的词向量(向量里的数值都是随机生成的)——这也就是掩码mask的操作,并依照时间段对其 一 一 进行词嵌入和位置编码。
在解码器部分,第一个时间段只有一个 < bos > 输入向量,对其进行Embedding操作和位置编码后,将编码器的输出信息和当前仅有< bos > 信息经过 masked self-attention,输出结果 “永”,在第二个时间段,解码器可以结合前面编码器的输出信息和后面 < bos >、“永” 两个词的信息来做运算,得到预测结果 “不”,同理,得到 “言”、“弃”,最后一个时间段,通过masked self-attention输出 < eos >,代表结束。


3.1 masked self-attention推导以及原理细节
我们首先有4个输入向量:
x
1
、
x
2
、
x
3
、
x
4
x^{1}、x^{2}、x^{3}、x^{4}
x1、x2、x3、x4,其中
x
1
、
x
2
x^{1}、x^{2}
x1、x2代表解码器已经输出的向量,它们是可以利用的,
x
3
、
x
4
x^{3}、x^{4}
x3、x4代表后面才能输出的向量,此时为向量的值为随机数值。masked self-attention的操作和普通的self-attention操作几乎一摸一样,具体步骤如下:

- 首先是所有的向量各自乘上 W q 、 W k 、 W v W_q、W_k、W_v Wq、Wk、Wv,得到向量 q 、 k 、 v q、k、v q、k、v
- 然后我们以 q 1 q^1 q1做query操作为例,这里的 q 1 q^1 q1会与 k 1 、 k 2 、 k 3 、 k 4 k^1、k^2、k^3、k^4 k1、k2、k3、k4分别做内积,计算注意力得分。
- 接着就是masked self-attention它独有的一个操作,就是把 x 3 、 x 4 x^3、x^4 x3、x4这两个不想要关注的向量对应的注意力得分 α \alpha α的值全部设置为负无穷。
- 对四个 α \alpha α 做softmax操作,进行归一化,得到 α 1 , 1 ′ 、 α 1 , 2 ′ 、 α 1 , 3 ′ 、 α 1 , 4 ′ \alpha^{'}_{1,1}、\alpha^{'}_{1,2}、\alpha^{'}_{1,3}、\alpha^{'}_{1,4} α1,1′、α1,2′、α1,3′、α1,4′,其中 α 1 , 1 ′ 、 α 1 , 2 ′ \alpha^{'}_{1,1}、\alpha^{'}_{1,2} α1,1′、α1,2′均有值,而 α 1 , 3 ′ 、 α 1 , 4 ′ \alpha^{'}_{1,3}、\alpha^{'}_{1,4} α1,3′、α1,4′的值均为0。
- 将 α ′ \alpha^{'} α′的值作为权重,所有的向量 v v v 按权相加求和,得到我们的最终输出结果 y 1 y^{1} y1, y 2 y^2 y2的操作和 y 1 y^1 y1一摸一样,而 y 3 、 y 4 y^3、y^4 y3、y4它们对应位置的 x x x 还不存在,故我们暂时先将其设置为0。
得到输出向量后,需要经过残差连接和层归一化,然后后面是一个self-attention层,这里的attention和编码器的attention不一样,这里的是cross-attention,它用来混合编码器和解码器的信息,cross attention 会用解码器生成的
q
q
q,去查询编码器生成的
k
k
k,一起计算注意力得分后,softmax会将编码器的向量
v
v
v按权相加,得到cross attention的输出结果,下面我们来了解一下具体操作:

- 我们假设 never say never 这句话它经过transformer编码器,变成了3个向量
- 解码器这边的5个向量会生成对应的 q q q向量,编码器这边的3个向量会生成对应的 k 、 v k、v k、v向量
- 我们永解码器这边的 q q q,去查询编码器这边的 k k k,即做一个内积的运算,得到注意力得分
- 接着经过softmax层,可以得到 α ′ \alpha^{'} α′, α ′ \alpha^{'} α′与对应的 v v v相乘后相加,即可得到我们的输出 y y y
这里我们是通过 q 1 q^1 q1进行查询的结果,同理可以得到 y 2 、 y 3 、 . . . y^2、y^3、... y2、y3、...,输入几个向量,cross attention 则输出几个向量,接着输出的结果继续做一个残差和层归一化操作,得到一批新的向量,然后再经过前馈神经网络层,随后再经过残差和层归一化操作,得到一批向量,将这组向量输入进 Linear 层,这层其实就是做一个线性回归,将输入的x乘上矩阵W,加上偏置项b, L i n e a r ( x ) = W x + b Linear(x)=Wx+b Linear(x)=Wx+b,目的是为了转换向量的维度,通过Linear层后的向量和输出的向量y的维度一致,最后所有的向量经过softmax操作,即可得到输出的向量,这个向量的每一个维度代表一个中文字出现的概率值,数字越大就代表这个字出现的可能性越大。我们可以将每个向量位置中,最大的值置为1,其余的置为0。
总结
本周再次回顾了Transformer文献,理解了Transformer的执行原理和流程,对self-attention和masked self-attention有了更深入了了解