数组
二分法
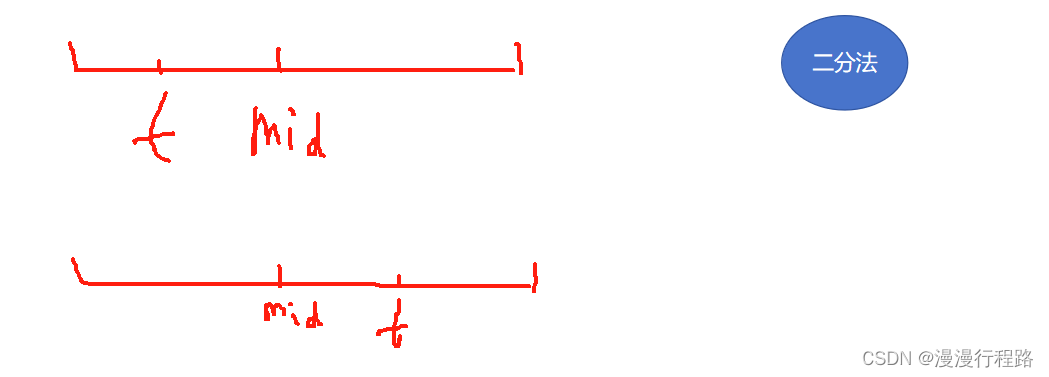
二分法满足从小到大排序无重复元素
1 两个边界,left,right
2 中间值的选择
3 边界问题考虑有两种
left <= right
当left <= right的时候,说明mid比较的时候已经比较了left right
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1
while left <= right:
mid = left + (right - left) // 2
if nums[mid] < target: # 中间值小于t,说明t在右边边界,这个时候需要移动左边界
left = mid + 1
elif nums[mid] > target: # 中间值小于t,说明t在mid左边,移动右边界
right = mid - 1
else:
return mid
return -1
left < right
当left < right的时候,说明比较的时候没有比较right
def search(self, nums: List[int], target: int) -> int:
left = 0
right = len(nums) - 1 # 左闭右开,所以right应该=len(nums)
while left < right:
mid = left + (right - left) // 2
if nums[mid] < target: # 中间值小于t,说明t在右边边界,这个时候需要移动左边界
left = mid + 1
elif nums[mid] > target: # 中间值小于t,说明t在mid左边,移动右边界
right = mid # 左闭右开区间,说明right判断的时候没有加入,所以需要加入right
else:
return mid
return -1
移除元素
移除数组中目标值相同的元素,还不能创建新的数组
这个时候使用快慢指针,慢指针负责指向不等于val的值,快指针负责找与val相同的值,然后进行更新
def removeElement(self, nums: List[int], val: int) -> int:
slow = 0
fast = 0
size = len(nums)
while fast < size:
if nums[fast] != val:
nums[slow] = nums[fast]
slow += 1
fast += 1
return slow
有序数组的平方
数组中存在正负数,所以这个时候往新数组里面存入的时候就需要比较,因为数组长度固定,所以新数组可以从后往前进行赋值,这样就会得到从小到大的排序
def sortedSquares(self, nums: List[int]) -> List[int]:
size = len(nums)
new = [0] * (size) # 创建新数组 新数组几个元素就乘以几
left,right = 0, size - 1
# 循环情况需要把长度数组都放一编,所以循环新数组即可
for i in range(size-1,-1,-1):
if nums[left]**2 > nums[right]**2:
new[i] = nums[left]**2
left += 1
else:
new[i] = nums[right]**2
right -= 1
return new
长度最小的子数组
数组里面找到长度最小的和等于目标值,数组值只用一次
从第一个开始找,找到和等于目标值之后继续从第二个开始,最后找出最小的长度
def minSubArrayLen(self, target: int, nums: List[int]) -> int:
# 两个快慢指针,慢的负责记录初始值,快的负责记录到目标值的长度之后继续前进
left,right = 0,0
size = len(nums)
minlen = float('inf')
newsum = 0
count = 0
while right < size:
newsum += nums[right] # 先开始加起来
while newsum >= target: # 因为有可能newsum的值很大,所以要不断的移动最左边
minlen = min(minlen,right-left + 1)
newsum -= nums[left]
left += 1
right += 1
return minlen if minlen != float('inf') else 0 # 不满足返回0
螺旋矩阵
螺旋矩阵主要是判断边界在哪里,规定好边界,一切迎刃而解

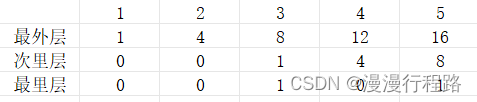
发现从3开始的奇数项,中间都有一个值,而且是居中的,所以可以通过长度来得到
发现从3开始,外层可以 8/4=2 12/4=3 16/4=4,那么是否可以推导n的外层就是x/4=n-1
所以我们是否可以每行都由n-1构成,这样就可以得到如下
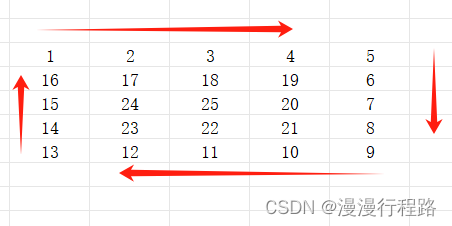
此时通过观察,不难发现如果要进行循环,那么是由n//2=2,这样发现可以循环几圈
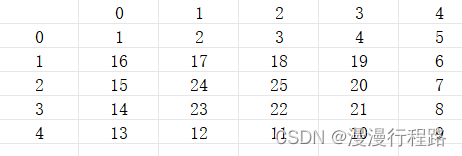
从左到右,00,01,02,03 -> 11,12 x不变 y 变
从上到下,04,14,24,34 -> 13,23 x变y不变
从右到左,44,43,42,41
从下到上,40,30,20,10
此时横坐标为i,纵坐标为j,这样就很容易写出四条循环来进行填充
动态规划
斐波那契数
1 确定dp数组及其下标含义
dp[i] 第i个数的斐波那契数为dp[i]
2 确定递推公式
dp[i] = dp[i-1] + dp[i-2]
3 初始化
dp[0]=0 dp[1]=1
4 确定遍历数序
发现后一项由前两项得到,所以从前往后遍历
5 验证
def fib(self, n: int) -> int:
dp = [0] * (n+1)
dp[0] = 0
dp[1] = 1
for i in range(2,n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
通过观察发现,一直变化的就两个变量
def fib(self, n: int) -> int:
if n <= 1:
return n
dp = [0,1]
for i in range(2,n+1):
temp = dp[0] + dp[1]
dp[0] = dp[1]
dp[1] = temp
return dp[1]
爬楼梯
爬楼梯每次可以爬一层,也可以爬两层,说明第三层由第一层和第二层得到
1 确定dp数字的下标及其含义
dp[i] 第i层的时候的方法数是dp[i]
2 确定递推公式
dp[i] 由dp[i-1] dp[i-2]得到
所以dp[i] = dp[i-1]+dp[i-2]
3 初始化
dp[1] = 1 dp[2] = 2
4 确定遍历顺序
由于第三层是由第一层跟第二层得到,所以顺序遍历
5 验证
def climbStairs(self, n: int) -> int:
dp = [0] * (n+1)
if n > 0 and n <=2:
return n
dp[1] = 1
dp[2] = 2
for i in range(3,n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
使用最小花费爬楼梯
1 确定dp数组及其下标含义
dp[i] 爬到第i阶楼梯所需的花费
2 确定递推公式
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
3 初始化
爬楼梯可以爬1层或两层
说明爬1层或两层的时候,他的价值就是cost[i],所以
dp[0] = 0 dp[1] = 0
4 确定遍历顺序
第三层楼梯是由前两层得到的,所以从前往后遍历
5 验证
def minCostClimbingStairs(self, cost: List[int]) -> int:
n = len(cost)
dp = [0] * (n+1)
dp[0] = 0
dp[1] = 0
for i in range(2,n+1):
dp[i] = min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2])
return dp[n]