【NC20313】仪仗队

news2024/9/30 3:33:37

题目

仪仗队

欧拉函数，找规律

思路

这好像是一道非常简单的找规律问题，所以你从 $1$ 开始枚举，计算出当 $N = i$ 时的结果 $ans_i$ ，所以你得出了以下结果：

N	ans
1	0
2	3
3	5
4	9
5	13
6	21
7	25
8	37

令人失望的是，并不能从中看出什么规律

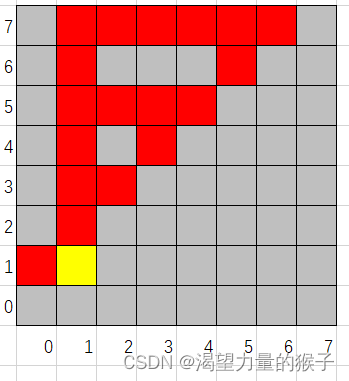
既然不能从最后的结果的数据中看出什么规律，那么就从模拟的情境中找规律，下面是 $N = 8$ 时的图（一个很明显的规律是整个方阵是对称的，所以只需要算其上三角或者下三角的个数，然后乘以 $2$ 即可，不过有一个特殊的位置（黄色格子）是始终需要加的，这也是除了 $N = 1$ 以外的结果都是奇数的原因）：

观察被染红的格子，从下到上，从左到右观察其行号和列号，可以发现，被染红格子的行号和列号是互质的。

因此，这道题的关键就是要计算小于等于 $k$ 的正整数中与 $k$ 互质的数的个数

用欧拉函数可解（倒不如说这道题就是在考察欧拉函数，简直量身定做）

什么是欧拉函数？

简而言之，欧拉函数是数论中的一个重要函数，表示小于等于 $n$ 的正整数中与 $n$ 互质的数的个数。通常用 $\phi(n)$ 表示

计算出了一半的个数（红色格子）后，将其乘以 $2$ 再加 $1$ 即可得出答案。

代码

#include <iostream>
using namespace std;

/**
 * @brief 初始化小于等于 n 的并与其互质的正整数个数
 *
 * @param phi phi数组，注意其长度为 n + 1，因为要将 0 除去
 * @param n 数组长度，其与 n 的关系为：len = n + 1
 */
void init_phi(int* phi, int len) {
    for (int i = 1; i < len; i++) {
        phi[i] = i;
    }
    for (int i = 2; i < len; i++) {
        if (phi[i] == i) {
            for (int j = i; j < len; j += i) {
                phi[j] -= phi[j] / i;
            }
        }
    }
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);
    int n = 0, ans = 0;
    cin >> n;
    if (n == 1) {
    	// 注意 1 要特殊处理
        cout << 0 << endl;
        return 0;
    }
    int phi[n + 1];
    init_phi(phi, n + 1);
    for (int i = 1; i < n; i++) {
        ans += phi[i];
    }
    cout << (ans << 1) + 1 << endl;
    return 0;
}