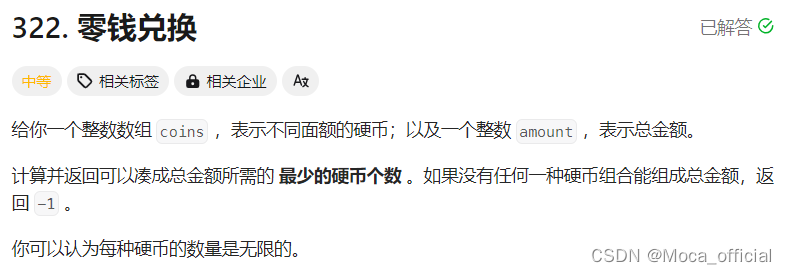
题目描述

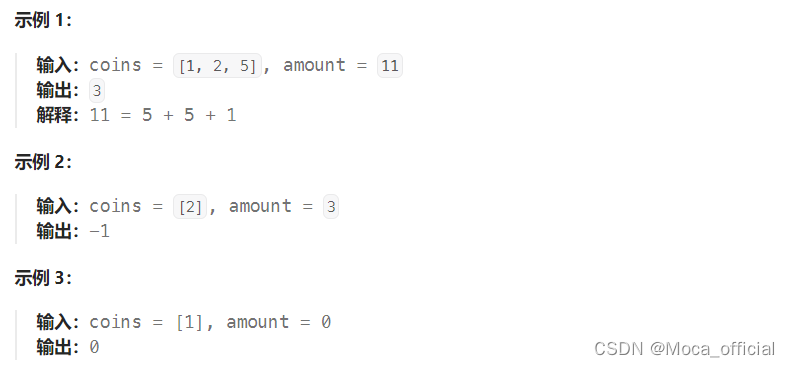
用例说明

思路讲解

动态规划五步法

第一步确定dp数组的含义：dp[i]为凑到金额为i所用最少的硬币数量

第二步确定动态规划方程：凑足金额为j-coins[i]所需最少的硬币个数为dp[j-coins[i]]，那凑足金额为j所用的最少硬币数为dp[j-coins[i]]+1

第三步初始化：凑足金额为0所需硬币数为0，即dp[0]=0

此外dp数组内其他值也需初始化为最大值，否则在遍历coins数组计算金额的时候容易被覆盖

第四步遍历顺序：外层遍历物品，内层遍历背包容量

第五步推导得出dp[amount]

代码

class Solution {
    public int coinChange(int[] coins, int amount) {
      int max=Integer.MAX_VALUE;
      int[] dp=new int[amount+1];
      for(int i=0;i<dp.length;i++){
        dp[i]=max;
      }
      dp[0]=0;
      for(int i=0;i<coins.length;i++){
        for(int j=coins[i];j<=amount;j++){
            if(dp[j-coins[i]]!=max){
                dp[j]=Math.min(dp[j],dp[j-coins[i]]+1);
            }
        }
      }
      return dp[amount]==max?-1:dp[amount];
    }
}

复杂度

时间复杂度O(n*amount)

空间复杂度O(amount)