目录
BSTree.h
框架
insert
insertR
find
findR
erase
eraseR
InOrder
拷贝构造
赋值重载
BSTree.h
框架
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
,_right(nullptr)
,_key(key)
{}
};
template<class K>
class BSTree
{
typedef BSTreeNode<K> node;
public:
private:
node* _root = nullptr;
};insert
1.在空位置插入,所以就要记录父节点
2.第一次插入时候要判断(_root == nullptr) 因为第一个节点没有父亲,我通过缺省参数初始化_root
3. node* parent = cur; parent初始化什么都可以,分析:与_root相同,则return,不同就延续cur
4.进行链接新节点,上面的while只是找到新节点在的父亲,parent与new node之前只是父子关系,左右孩子还关系需要比较_key的值
5.返回的值是bool,因为BSTree的结构和插入顺序有关
bool insert(const K& key)
{
if (_root == nullptr)
{
_root = new node(key);
return true;
}
node* cur = _root;
node* parent = cur;
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
return false;
}
}
if (parent->_key < key)
parent->_right = new node(key);
else
parent->_left = new node(key);
return true;
}insertR
通过循环来插入
1.通过 & 就可以直接与父节点链接上,分析:上一个栈帧里root的指向,当前的root的地址,执行到nullptr时候,root所存放的值就是new 出来节点的地址,这样就链接上了
2.仍然是在nullptr的位置插入、
3.对于返回值(函数出口)来说,两个地方:new出来了就是true,相等就是false,其他递归均是过程
4. _insertR(root->_right, key);仔细想了想,这个地方也是返回,不然最后返回的时候没有返回值啊,但是也不报错,也没有警告(vs编译器会自动处理函数的返回值 ,不是像oj上那样 每个返回路径都需要严格加return)但还是加上有味道(因为这是不同的栈帧,不是循环)
bool insertR(const K& key)
{
return _insertR(_root, key);
}
bool _insertR(node*& root, const K& key)
{
if (root == nullptr)
{
root = new node(key);
return true;
}
if (root->_key < key)
{
return _insertR(root->_right, key);
}
else if (root->_key > key)
{
return _insertR(root->_left, key);
}
else
{
return false;
}
}find
bool find(const K& key)
{
node* cur = _root;
while (cur)
{
if (cur->_key == key)
{
return true;
}
else if (cur->_key < key)
{
cur = cur->_right;
}
else if (cur->_key > key)
{
cur = cur->_left;
}
}
return false;
}findR
1.返回的是能否找到,即bool
2.函数出口nullptr 返回false,相等返回 true
3.&可以有也可以没有,其一:这里的值拷贝只是一个指针,其二:不需要有链接关系
bool findR(const K& key)
{
return _findR(_root, key);
}
bool _findR(node* root, const K& key)//不起到链接作用,但引用也是可以的
{
if (root == nullptr) return false;
if (root->_key < key)
{
return _findR(root->_right, key);
}
else if (root->_key > key)
{
return _findR(root->_left, key);
}
else
{
return true;
}
}erase
分析:
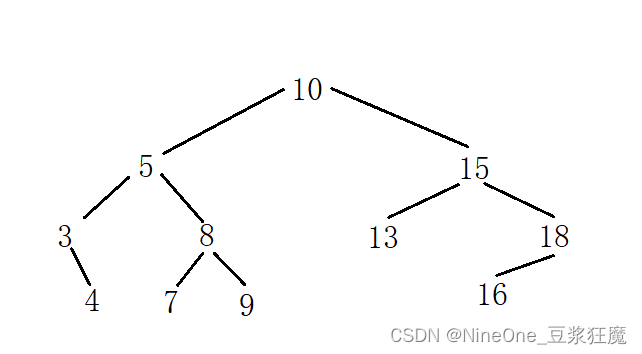
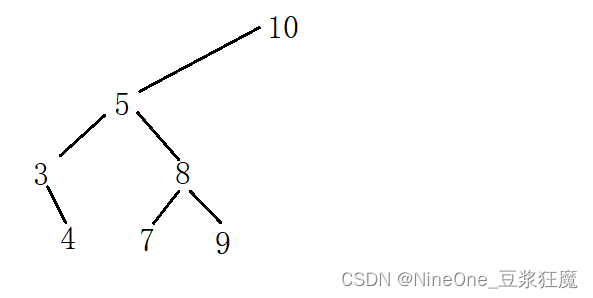
1.删3,3的左为空,就需要将3的右给5的左(叶子节点也算在在里面)
2.删18,18的右为空,就需要将18的左给15的右(叶子节点也算在里面)
3.删5,那么就需要有值来代替5,符合条件的是左树的最大节点,或右树的最小节点,随之转换删除的是4或7,而不是5了
4.在右边这种情况,当然也可以选择,与9交换,然后删9,但是直接将_root转换为5更舒服
代码注意事项:
1.对于1和2两种删除的情况,因他们可以有儿子,所以需要借助父亲,链接上他们的儿子
2.如果只有一个节点,在清除语句的第一个if,会将_root置空
3.找到的待删除的值,与父亲只有链接关系,链接到左还是右,还需要通过指针进一步判断
4.pmaxleft需要初始化成当cur(不能为nullptr),因为maxleft = pmaxleft -> _left,如果,maxleft没有右树,pmaxleft为空,那么maxleft就找不到父亲,在解引用的时候就会报错,这种情况也正好是pmaxleft->_left == maxleft,其他情况都是右树(也就是while进去了)
5.当左右都不为空的时候 del 需要改成maxleft,因为只是交换了值,cur还在原来位置,不然下面的节点就全丢了
bool erase(const K& key)
{
node* cur = _root;
node* parent = cur;
while (cur)
{
if (cur == nullptr) return false;
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
break; //等于准备删除
}
}
if (cur == nullptr) return false;// 空就是没找到
node* del = cur;
if (cur->_left == nullptr)
{
if (cur == _root)
{
_root = cur->_right;
}
if (parent->_left == cur)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
else if (cur->_right == nullptr)
{
if (cur == _root)
{
_root = cur->_left;
}
if (parent->_left == cur)
{
parent->_left = cur->_left;//这个地方 ; 没写,报编译器内部错误
}
else
{
parent->_right = cur->_left;
}
}
else
{
node* pmaxleft = cur;
node* maxleft = cur->_left;
while (maxleft->_left)
{
pmaxleft = maxleft;
maxleft = maxleft->_right;
}
cur->_key = maxleft->_key;
if (pmaxleft->_left == maxleft)
{
pmaxleft->_left = maxleft->_right;
}
else
{
pmaxleft->_right = maxleft->_right;
}
del = maxleft;//因为只是换的节点的值
}
delete del;
return true;
}eraseR
1.通过循环解决,删除操作本身就需要链接,&很合适
2.如果为nullptr就是没有对应的值,返回false
3.仔细分析下,是怎么删3的,和怎么链接的
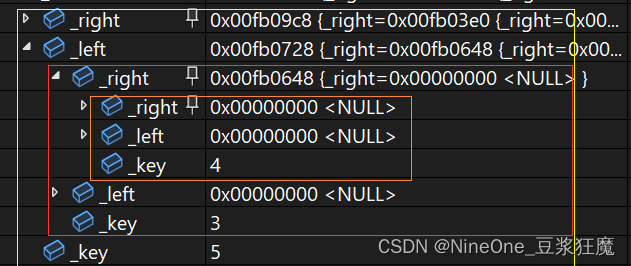
这是我第一次画的,其实这个root写在这个位置,并不是很好
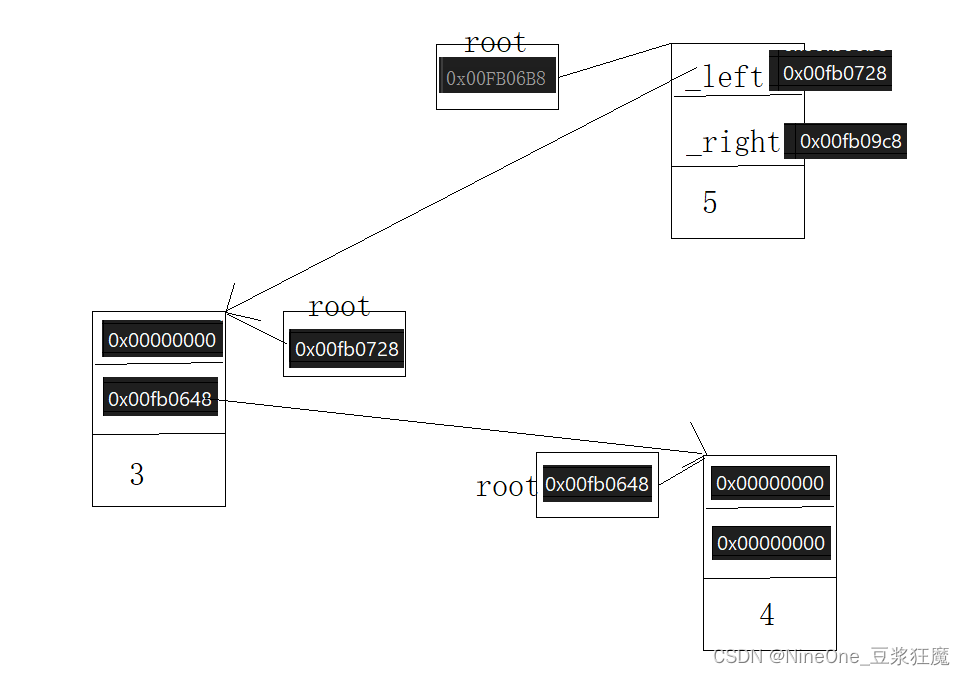
应该是这样:在引用传参的时候传的就是5节点里_left,再次进入一个栈帧root->_right就是节点4的地址(需要沉淀一下,从调试的结果是这样的)对于&root自然是在节点10里,因为10->_left存放的是5节点的地址
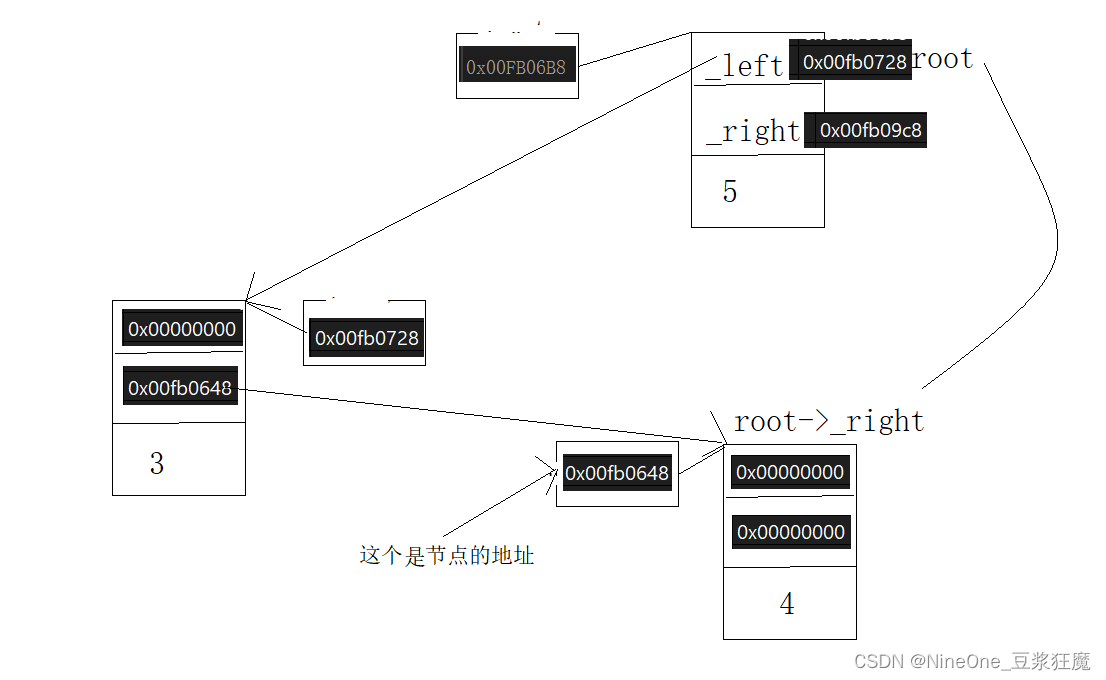
bool eraseR(const K& key)
{
return _eraseR(_root, key);
}
bool _eraseR(node*& root, const K& key)
{
if (root == nullptr) return false;
if (root->_key < key)//找的过程
{
_eraseR(root->_right, key);
}
else if (root->_key > key)
{
_eraseR(root->_left, key);
}
else//找到
{
node* del = root;
if (root->_left == nullptr)
{
root = root->_right;//赋值重载,就是要只拷贝
}
else if (root->_right == nullptr)
{
root = root->_left;
}
else
{
node* pminright = root;
node* minright = root->_right;
while (minright->_left)
{
pminright = minright;
minright = minright->_left;
}
swap(minright->_key, root->_key);
return _eraseR(root->_right, key);
}
delete del;
return true;
}
}InOrder
中序遍历
void InOrder()
{
_InOrder(_root);
cout << endl;
}
void _InOrder(node* root)
{
if (root == nullptr) return;
_InOrder(root->_left);
cout << root->_key << " ";
_InOrder(root->_right);
}拷贝构造
copy例不能把tmp换成_root,不然每一次递归_root都会被覆盖,链接不上,而tmp每次都是一个新的
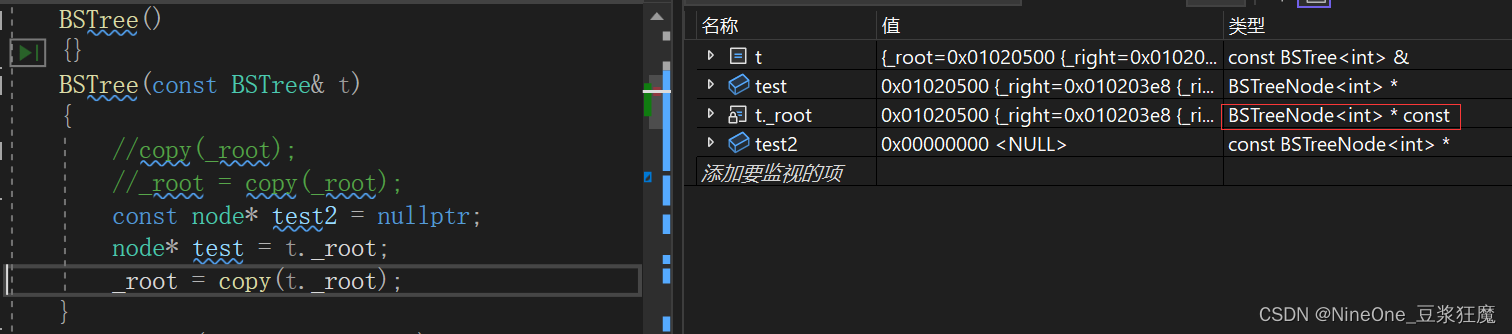
问题:t是const,那么t._root也是const,为什么copy里的t不需要const修饰
node*可以接收node*const,而且下面的copy里的const怎么加都不影响
比如:node* test = t._root;这是被允许的,这只是一个赋值;node*& test = t._root;这样就不行,关键:因为我只是用了他的值,它加了const只是不能修改它,但是可以去他的值
BSTree(const BSTree<K>& t)
{
_root = copy(t._root);
}
node* copy(node* t)
{
if (t == nullptr) return nullptr;
node* tmp = new node(t->_key);
tmp->_left = copy(t->_left);
tmp->_right = copy(t->_right);
return tmp;
}赋值重载
我遇到的问题:这个改正了我之前错误的理解:我之前认为这里的t是不会被析构的,因为他是在堆上的,在栈上出了作用域会自己弹掉;但是t(t是拷贝构造出来的)出了这个函数作用域就被应该销毁(这是我在调试的时候看到的),而且堆不就是要被析构吗,
问题就在swap上:swap没有吧t._root换掉就会被析构掉,导致_root也没了,所以要把t._root置空
//①用不用std里的会用自己写的,就会无限递归
//②void swap(node*& t)和void swap(node* t)会调用不明确
void swap(node*& t)// 因为这里的t会被析构掉,它已经出了它的函数作用域
{// 这也是为什么刚进入析构_root就是nullptr,所以这个t必须是&传参,要换掉这个t
//swap(_root, t);
std::swap(_root, t);
}
void swap(node** t)//和swap(&t._root)对应
{
std::swap(_root, *t);
}
//void swap(node* t)//和swap(t._root)对应,传拷贝的也不是不可以,出去之后要把t._root改成nullptr☆
//{
// std::swap(_root, t);
//}
//BSTree<K>& operator=(const BSTree<K> t)//swap掉不了
BSTree<K>& operator=(BSTree<K> t)//
{
//swap(&t._root);//就是要改掉原来的t ->void swap(node** t)
swap(t._root);
t._root = nullptr;
//swap(_root, t._root);//可以
return *this;
}