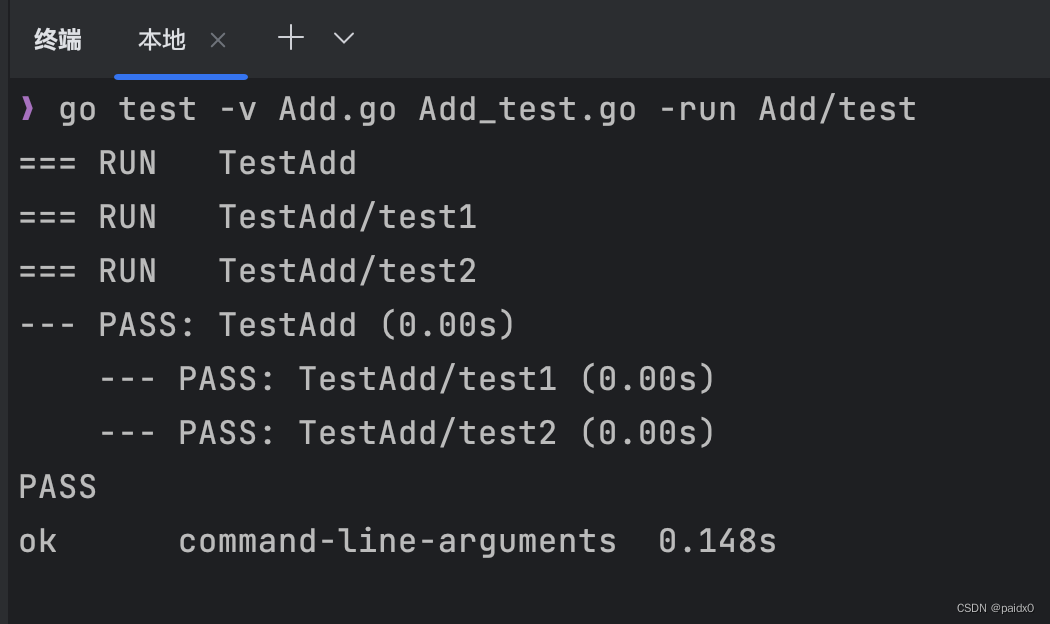
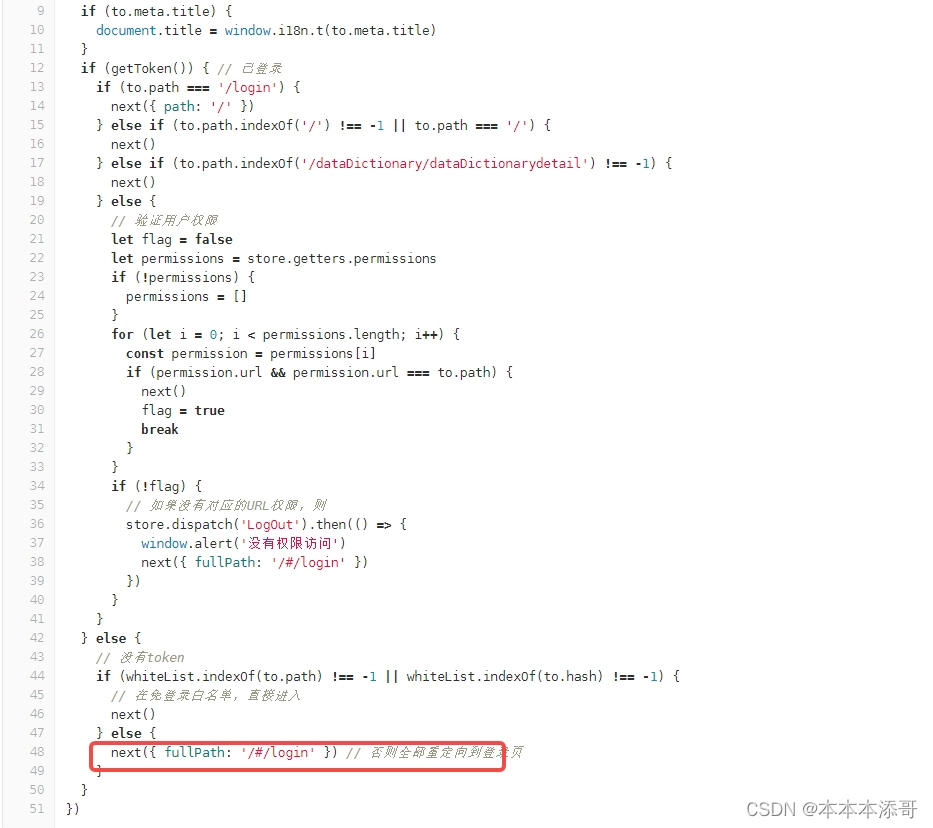
1、计算冒泡排序的空间复杂度

答案:该程序空间复杂度为O(1)。
解析:该程序在栈空间所申请的临时变量空间只有三个,也就是看成常数个,所以是O(1)。如下图所示
2、动态开辟N个数的数组空间复杂度

答案:该程序空间复杂度为O(N).
解析:因为该程序动态开辟了N+1个空间,属于O(N)这个量级,1可忽略,所以空间复杂度为O(N)。
3、计算阶乘递归的空间复杂度

答案:该程序空间复杂度为O(N)。
解析:因为每递归一次就申请一个空间,递归了N次所以申请了N个空间,所以是O(N)。
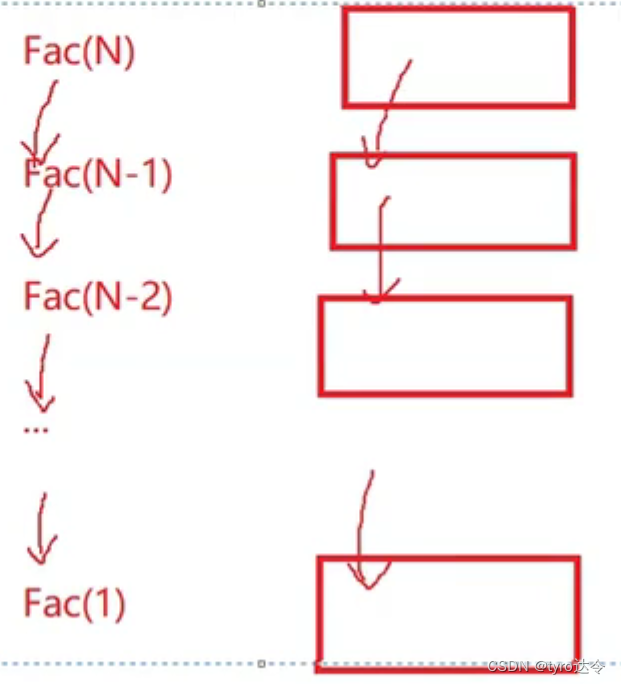
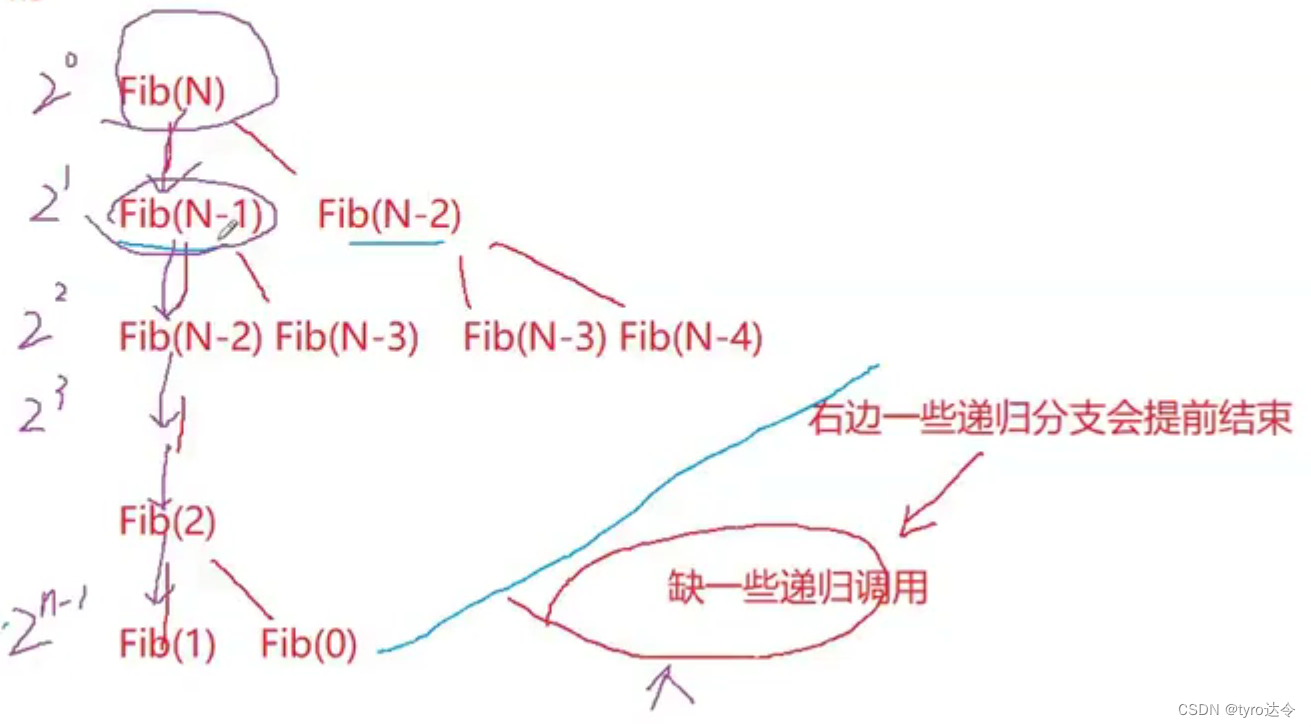
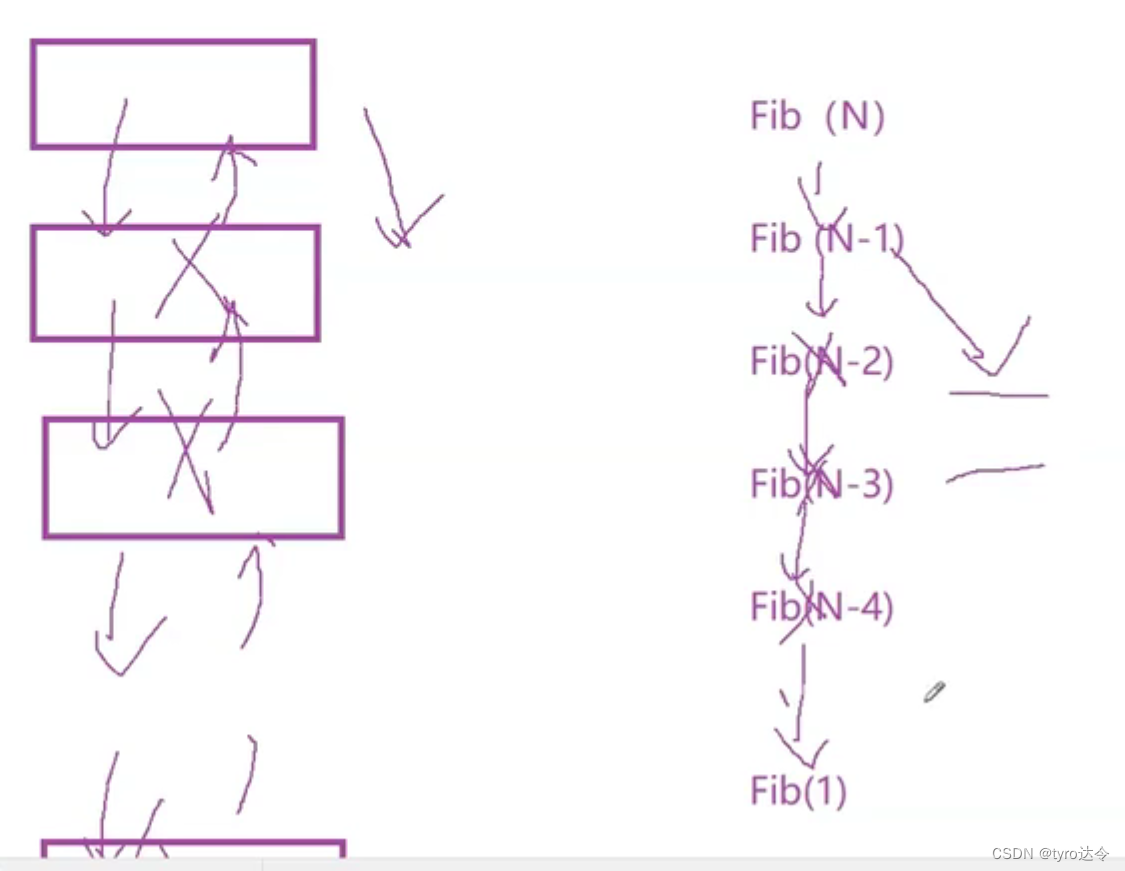
4、计算斐波那契递归的空间复杂度

答案:空间复杂度为O(N)。
解析:Fib依次申请空间,从Fib(N)申请到Fib(1),共申请了N个空间。假设虽然Fib(N)递归一次变为Fib(N-1)和Fib(N-2),看起来需要两个空间,可是将一个空间申请给Fib(N-1),等返回后这个空间就会销毁,然后再将这个空间申请给Fib(2),空间重复利用,每次递归都以此类推。所以每递归一次只需开辟一个空间,而不是每递归一次就要开辟2倍的空间。
总结
空间是可以重复利用,不累计的;
时间是一去不复还,累计的。