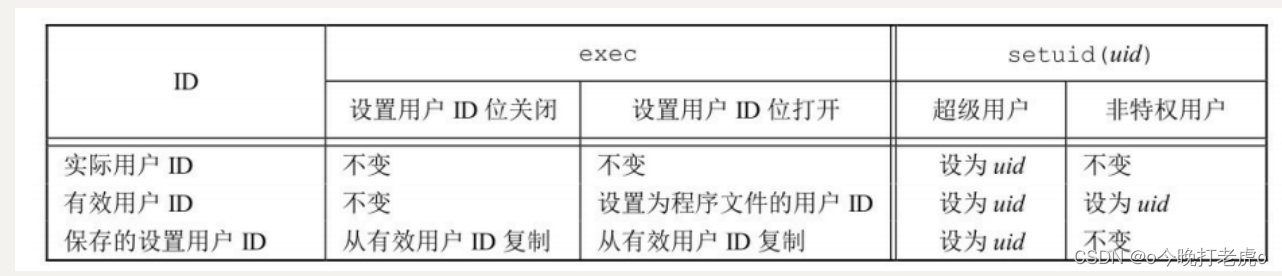
Backpropagation反向传播
我们上节课学习了深度学习,也知道采用梯度下降优化我们的各神经元参数,以语音识别为例,一个输入特征量1000多项,8层隐层,大致需要的w,b参数有数百万项,这样我们梯度下降的计算量是非常大的,我们为了让梯度下降计算的更有效率,我们才有反向传播的方法

插图1
链式法则chain rule
我们学过微积分的话,下图应该不难理解,不赘述,看图

插图2
我们计算神经网络损失函数时候,把函数输出
和目标值
的距离评估
(可以是交叉熵)在所有样本上求和而成,我们为了梯度下降,就需要求解w的偏微分,就变成了每个样本C的对w的偏微分和。

插图3
我们考虑一个神经元,假设就2个输入x1,x2,我们很容易就得出神经元的输出z,经过激活函数(sigmoid或Relu)输出传递给其他神经元。我们求C对w的偏导,根据链式法则,就得到2个偏微分的乘积,其中把
的计算参数称作前向传播,把
计算称作反向传播

插图4
当然z对w1,w2的偏微分是秒算的,分别是x1,x2,即w对应连结的值

插图5
如图我们把第一层输入给定后,第一层神经元的偏微分就可以求出,同时算出的激活函数输出即下一级神经元的偏微分,从左至右,一级一级下去

插图6
我们假设一个神经元激活函数前后分别是z,a,如果是sigmoid函数,那当然
,而a又可以为下一级神经元作为输入,经权重偏置计算的到Z',Z'',我们求C对z的偏微分就可以经过链式法则,a对z的偏微分就是sigmoid(z)的导数,我们很熟悉,而后者可以展开成图最后的式子,当然Z',Z''对a的偏微分就是w3,w4,但是C对Z',Z''的偏微分怎么求呢,只要还有下一级神经元,我们就需要再往下一级计算(事实上类似于递归的算法)

插图7
我们将神经元考虑成一个反向模型,输入是C对Z',Z''的偏导,由于这个神经元的参数已经确定了,所以符号采用了三角号
插图8
我们假设当前的神经元已经是最后一个,即输出就是准备送给计算损失函数的,那我们根据下图就可以求出C对Z',Z''的偏微分了,一个是激活函数对其的偏微分,另一个是根据你定义的损失函数模型的偏微分(可求)

插图9
我们假设当前神经元连结的不是输出层,即连接的还是神经元,我们为了求出当前的偏导就需要用到下一级的偏导,直到传递到输出层,和递归很向吧。其实就相当于从末尾的输出端往左侧输入端一级一级传递,所以是反向传播

插图10
我们最后总结下,为了计算z对w的偏导,我们使用前向传播,计算出每一级输出即可
为了计算出损失函数对z的误差,我们使用反向传播
最后将2者相乘就得出了损失函数对于w的偏微分,实现了梯度下降的梯度求法。
(老师说不懂这里也可以,但是我觉得这部分理解其实并不难,还是掌握比较好)

插图11