【CPP】C++11多线程

news2024/9/22 10:07:00

thread类

在C++11之前，涉及到多线程问题，都是和平台相关的，比如windows和linux下各有自己的接口，这使得代码的可移植性比较差。C++11中最重要的特性就是对线程进行支持了，使得C++在并行编程时不需要依赖第三方库，而且在原子操作中还引入了原子类的概念。要使用标准库中的线程，必须包含< thread >头文件

构造

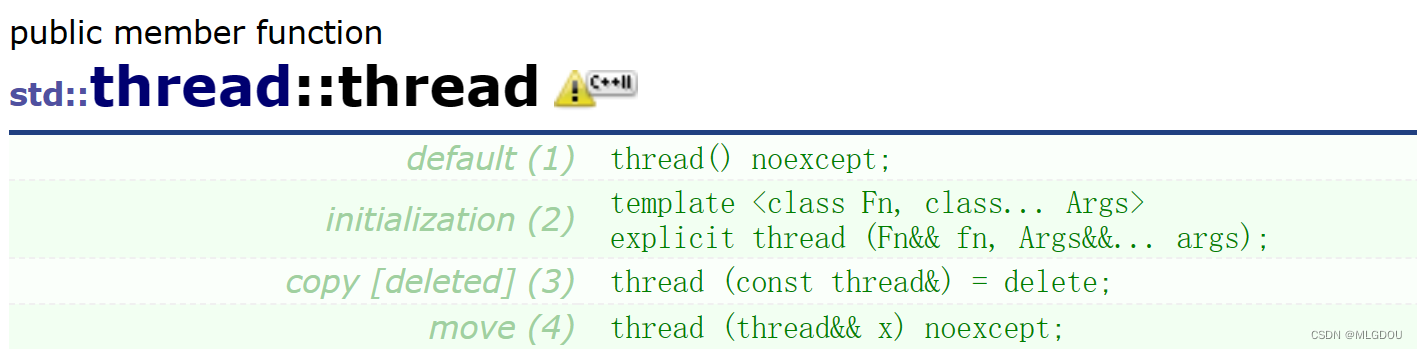
在这里插入图片描述
我们可以看到thread类不支持拷贝构造（delete关键词表示声明了某函数但禁止被使用，在编译时会直接报错），但支持传右值引用和完美转发。第一个参数是线程创建调用的函数，第二个是可变参数列表，支持传递多个参数。
举个例子

#include<thread>
#include<iostream>

using namespace std;
void Func(int n,int num)
{
	for (int i = 0; i < n; i++)
	{
		cout << num<<":"<<i << endl;
	}
	cout << endl;
}

int main()
{
	
	//thread t1(Func, 10,1);
	cin>>n;
	thread t1([n](int num){
	for(int i=0;i<n;i++)
	{
		cout<<num<<":"<<i<<endl;
	},n);
	thread t2(Func, 20,2);

	t1.join();
	t2.join();

	return 0;
}

当然这里func也可以换成lambda表达式，其次thread类虽然不支持拷贝构造，但支持移动构造和赋值。

namespace this_thread

在这里插入图片描述

yield

在这里插入图片描述
implementation:实施，实行
当一个线程调用此函数，将它的时间片交还给操作系统，让操作系统reschedule调度，从而避免阻塞等待。

mutex类

问题引入

看下面这段代码

int x = 0;
void func(int n)
{
	for (int i = 0; i < n; i++)
		x += 1;
}

int main()
{
	thread t1(func, 10000);
	thread t2(func, 20000);

	t1.join();
	t2.join();

	cout << x << endl;
	return 0;
}

按理来说执行结果应该是30000，但实际上执行结果不但不为30000，而且每次还不一样。
在这里插入图片描述

解决方案

在这里插入图片描述
定义一个全局的锁，在每一次对全局变量x++的时候互斥访问临界资源

成员函数

在这里插入图片描述

lockguard

template<class Lock>
class LockGuard
{
public:
	LockGuard(Lock& lk)
		:_lk(lk)
	{
		_lk.lock();
	}

	~LockGuard()
	{
		_lk.unlock();
	}

private:
	Lock& _lk //成员变量可以是引用，但必须在初始化列表初始化
};

但程序抛异常时，可能来不及释放锁，就被catch了，进而会造成死锁状态，用RAII的方式lock_guard会在作用域结束时由编译器自动调用析构函数
在这里插入图片描述

条件变量

实现两个线程交替打印1到100的数

//两个线程交替分别打印奇数和偶数
int main()
{
	mutex mtx;
	condition_variable cond;
	int n = 100;
	int x = 1;

	thread t1([&, n]() {
		while (x < n)
		{
			unique_lock<mutex> lock(mtx);
			if (x % 2 == 0)//打印奇数，偶数阻塞
				cond.wait(lock);
			cout << this_thread::get_id() << ":"<<x++<<endl;
			cond.notify_one();
		}
		});
	thread t2([&, n]() {
		while (x < n)
		{
			unique_lock<mutex> lock(mtx);
			if (x % 2 != 0)
				cond.wait(lock);
			cout << this_thread::get_id() <<":"<<x++<< endl;
			cond.notify_one();
		}
		});

	t1.join();
	t2.join();
	return 0;
}