参考资料:
(1)贝塞尔曲线法
(2)曲线杂谈(二):Bezier曲线的特殊性质
贝塞尔曲线法
1 算法概述
1.1 算法简介
- 贝塞尔曲线于1962年由法国工程师皮埃尔·贝塞尔(Pierre Bézier)所广泛发表,他运用贝塞尔曲线(可视化)来为汽车的主体进行设计。
- 贝塞尔曲线是应用于二维图形应用程序的数学曲线,由一组称为控制点的向量来确定,给定的控制点按顺序连接构成控制多边形,贝塞尔曲线逼近这个多边形,进而通过调整控制点坐标改变曲线的形状。
1.2 算法思想
对于车辆系统,规划的轨迹应满足以下准则:
① 轨迹连续
② 轨迹曲率连续
③ 轨迹容易被车辆跟随
④ 容易生成
给定
n
+
1
n+1
n+1个数据点,
p
0
−
p
n
p_0-p_n
p0−pn,生成一条曲线,使得该曲线与这些点描述的形状相符。
2 算法原理
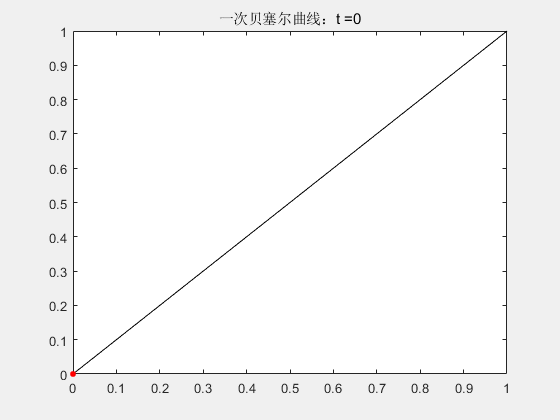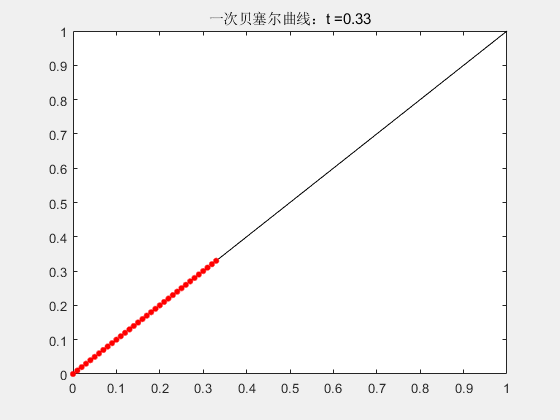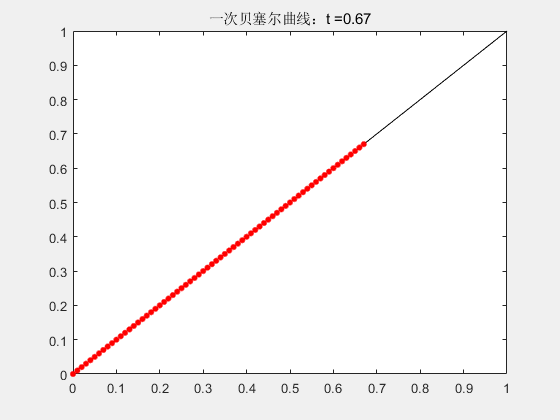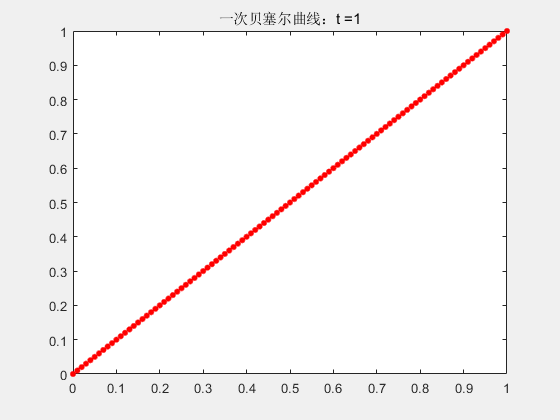
2.1 一阶贝塞尔曲线
一阶贝塞尔曲线需要2个控制点,假设分别为
P
0
P_0
P0,
P
1
P_1
P1。则贝塞尔曲线上的生成点
p
1
(
t
)
p_1(t)
p1(t)可以表达为:
p
1
(
t
)
=
P
0
+
(
P
1
−
P
0
)
t
→
p
1
(
t
)
=
(
1
−
t
)
P
0
+
t
P
1
t
∈
[
0
,
1
]
p_{1}(t)=P_{0}+\left(P_{1}-P_{0}\right) t \rightarrow p_{1}(t)=(1-t) P_{0}+t P_{1} \\ t∈[0,1]
p1(t)=P0+(P1−P0)t→p1(t)=(1−t)P0+tP1t∈[0,1]
一阶曲线就是根据t来的线性插值。
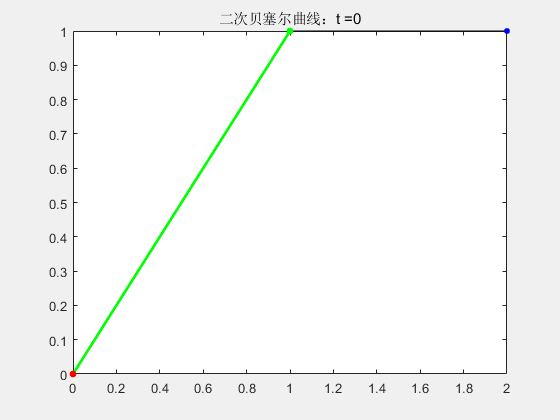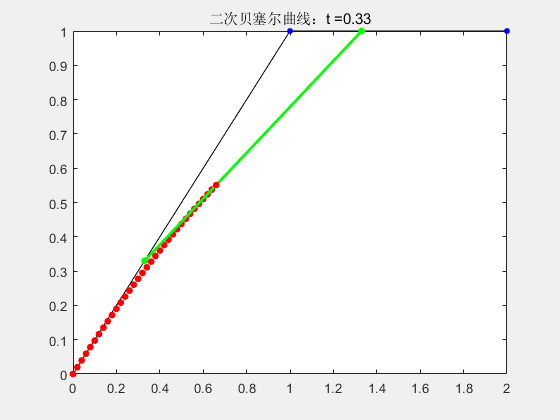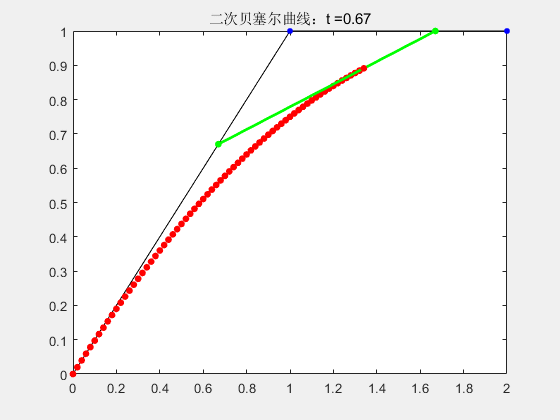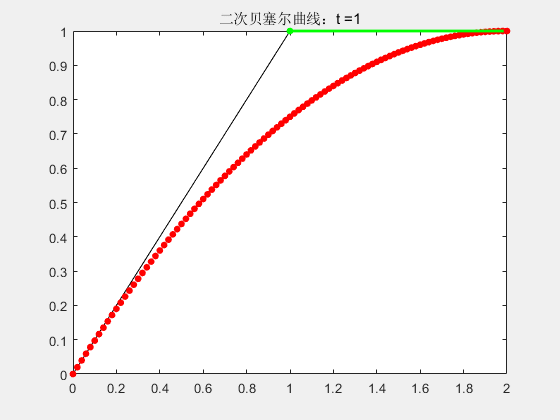
2.2 二阶贝塞尔曲线
二阶贝塞尔曲线需要3个控制点,假设分别为
P
0
P_0
P0,
P
1
P_1
P1,
P
2
P_2
P2。
P
0
P_0
P0和
P
1
P_1
P1构成一阶,
P
1
P_1
P1和
P
2
P_2
P2构成一阶:
{
p
1
,
1
(
t
)
=
(
1
−
t
)
P
0
+
t
P
1
p
1
,
2
(
t
)
=
(
1
−
t
)
P
1
+
t
P
2
\left\{\begin{array}{l} p_{1,1}(t)=(1-t) P_{0}+t P_{1} \\ p_{1,2}(t)=(1-t) P_{1}+t P_{2} \end{array}\right.
{p1,1(t)=(1−t)P0+tP1p1,2(t)=(1−t)P1+tP2
在生成的两个一阶点基础上,可以生成二阶贝塞尔点:
p
2
(
t
)
=
(
1
−
t
)
p
1
,
1
+
t
p
1
,
2
p_{2}(t)=(1-t) p_{1,1}+t p_{1,2}
p2(t)=(1−t)p1,1+tp1,2
则贝塞尔点与3个控制点的关系为:
p
2
(
t
)
=
(
1
−
t
)
2
P
0
+
2
t
(
1
−
t
)
P
1
+
t
2
P
2
t
∈
[
0
,
1
]
p_{2}(t)=(1-t)^{2} P_{0}+2 t(1-t) P_{1}+t^{2} P_{2} \\ t∈[0,1]
p2(t)=(1−t)2P0+2t(1−t)P1+t2P2t∈[0,1]
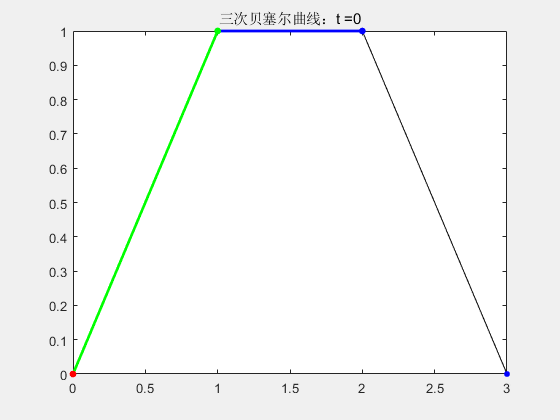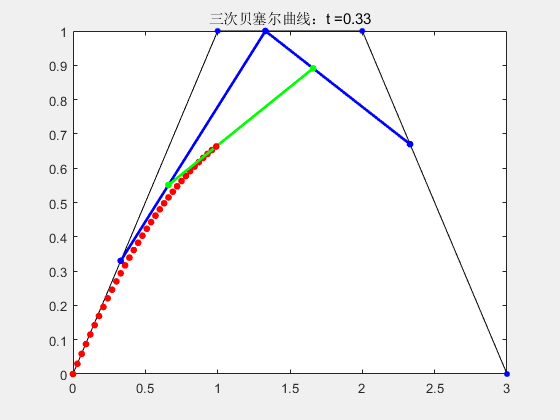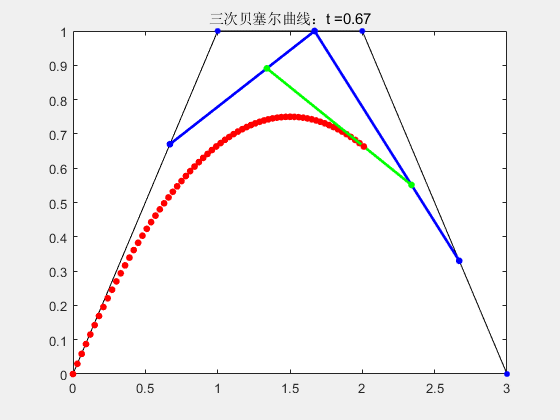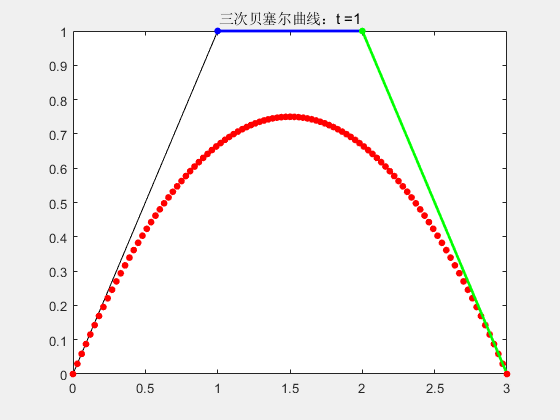
2.3 三阶贝塞尔曲线
三阶贝塞尔曲线有4个控制点,假设分别为
P
0
P_0
P0,
P
1
P_1
P1,
P
2
P_2
P2,
P
3
P_3
P3,
P
0
P_0
P0和
P
1
P_1
P1、
P
1
P_1
P1和
P
2
P_2
P2、
P
2
P_2
P2和
P
3
P_3
P3都构成一阶:
{
p
1
,
1
(
t
)
=
(
1
−
t
)
P
0
+
t
P
1
p
1
,
2
(
t
)
=
(
1
−
t
)
P
1
+
t
P
2
p
1
,
3
(
t
)
=
(
1
−
t
)
P
2
+
t
P
3
\left\{\begin{array}{l} p_{1,1}(t)=(1-t) P_{0}+t P_{1} \\ p_{1,2}(t)=(1-t) P_{1}+t P_{2} \\ p_{1,3}(t)=(1-t) P_{2}+t P_{3} \end{array}\right.
⎩
⎨
⎧p1,1(t)=(1−t)P0+tP1p1,2(t)=(1−t)P1+tP2p1,3(t)=(1−t)P2+tP3
在生成的三个一阶点基础上,可以生成两个二阶贝塞尔点:
{
p
2
,
1
(
t
)
=
(
1
−
t
)
p
1
,
1
+
t
p
1
,
2
p
2
,
2
(
t
)
=
(
1
−
t
)
p
1
,
2
+
t
p
1
,
3
\left\{\begin{array}{l} p_{2,1}(t)=(1-t) p_{1,1}+t p_{1,2} \\ p_{2,2}(t)=(1-t) p_{1,2}+t p_{1,3} \end{array}\right.
{p2,1(t)=(1−t)p1,1+tp1,2p2,2(t)=(1−t)p1,2+tp1,3
在生成的两个二阶点基础上,可以生成三阶贝塞尔点:
p
3
(
t
)
=
(
1
−
t
)
p
2
,
1
+
t
p
2
,
2
p_{3}(t)=(1-t) p_{2,1}+t p_{2,2}
p3(t)=(1−t)p2,1+tp2,2
即:
p
3
(
t
)
=
(
1
−
t
)
3
P
0
+
3
t
(
1
−
t
)
2
P
1
+
3
t
2
(
1
−
t
)
P
2
+
t
3
P
3
p_{3}(t)=(1-t)^{3} P_{0}+3 t(1-t)^{2} P_{1}+3 t^{2}(1-t) P_{2}+t^{3} P_{3}
p3(t)=(1−t)3P0+3t(1−t)2P1+3t2(1−t)P2+t3P3

2.4 n阶贝塞尔曲线
对于
P
0
,
P
1
,
P
2
,
…
,
P
n
P_{0}, P_{1}, P_{2}, \ldots, P_{n}
P0,P1,P2,…,Pn共
n
+
1
n+1
n+1个控制点而言,贝塞尔点定义为:
p
n
(
t
)
=
∑
i
=
0
n
C
n
i
⋅
(
1
−
t
)
n
−
i
⋅
t
i
⋅
P
i
=
∑
i
=
0
n
B
i
,
n
(
t
)
⋅
P
i
p_{n}(t)=\sum_{i=0}^{n} C_{n}^{i} \cdot(1-t)^{n-i} \cdot t^{i} \cdot P_{i}=\sum_{i=0}^{n} B_{i, n}(t) \cdot P_{i}
pn(t)=i=0∑nCni⋅(1−t)n−i⋅ti⋅Pi=i=0∑nBi,n(t)⋅Pi
其中,
B
i
,
n
(
t
)
=
C
n
i
⋅
(
1
−
t
)
n
−
i
⋅
t
i
B_{i, n}(t)=C_{n}^{i} \cdot(1-t)^{n-i} \cdot t^{i}
Bi,n(t)=Cni⋅(1−t)n−i⋅ti称为伯恩斯坦基函数。伯恩斯坦基函数的一阶导数为:
B
i
,
n
′
(
t
)
=
[
C
n
i
⋅
(
1
−
t
)
n
−
i
⋅
t
i
]
′
=
n
!
i
!
⋅
(
n
−
i
)
!
⋅
[
−
(
n
−
i
)
⋅
(
1
−
t
)
n
−
i
−
1
⋅
t
i
+
i
⋅
t
i
−
1
⋅
(
1
−
t
)
n
−
i
]
=
n
!
i
!
⋅
(
n
−
i
)
!
⋅
i
⋅
t
i
−
1
⋅
(
1
−
t
)
n
−
i
−
n
!
i
!
⋅
(
n
−
i
)
!
⋅
(
n
−
i
)
⋅
(
1
−
t
)
n
−
i
−
1
⋅
t
i
=
n
(
n
−
1
)
!
(
i
−
1
)
!
⋅
(
n
−
i
)
!
t
i
−
1
⋅
(
1
−
t
)
n
−
i
−
n
(
n
−
1
)
!
i
!
⋅
(
n
−
i
−
1
)
!
⋅
(
1
−
t
)
n
−
i
−
1
⋅
t
i
=
n
C
n
−
1
i
−
1
t
i
−
1
⋅
(
1
−
t
)
n
−
i
−
n
C
n
−
1
i
(
1
−
t
)
n
−
i
−
1
⋅
t
i
=
n
[
B
i
−
1
,
n
−
1
(
t
)
−
B
i
,
n
−
1
(
t
)
]
\begin{array}{l} B_{i, n}^{\prime}(t)=\left[C_{n}^{i} \cdot(1-t)^{n-i} \cdot t^{i}\right]^{\prime} \\ =\frac{n !}{i ! \cdot(n-i) !} \cdot\left[-(n-i) \cdot(1-t)^{n-i-1} \cdot t^{i}+i \cdot t^{i-1} \cdot(1-t)^{n-i}\right] \\ =\frac{n !}{i ! \cdot(n-i) !} \cdot i \cdot t^{i-1} \cdot(1-t)^{n-i}-\frac{n !}{i ! \cdot(n-i) !} \cdot(n-i) \cdot(1-t)^{n-i-1} \cdot t^{i} \\ =n \frac{(n-1) !}{(i-1) ! \cdot(n-i) !} t^{i-1} \cdot(1-t)^{n-i}-n \frac{(n-1) !}{i ! \cdot(n-i-1) !} \cdot(1-t)^{n-i-1} \cdot t^{i} \\ =n C_{n-1}^{i-1} t^{i-1} \cdot(1-t)^{n-i}-n C_{n-1}^{i}(1-t)^{n-i-1} \cdot t^{i}=n\left[B_{i-1, n-1}(t)-B_{i, n-1}(t)\right] \end{array}
Bi,n′(t)=[Cni⋅(1−t)n−i⋅ti]′=i!⋅(n−i)!n!⋅[−(n−i)⋅(1−t)n−i−1⋅ti+i⋅ti−1⋅(1−t)n−i]=i!⋅(n−i)!n!⋅i⋅ti−1⋅(1−t)n−i−i!⋅(n−i)!n!⋅(n−i)⋅(1−t)n−i−1⋅ti=n(i−1)!⋅(n−i)!(n−1)!ti−1⋅(1−t)n−i−ni!⋅(n−i−1)!(n−1)!⋅(1−t)n−i−1⋅ti=nCn−1i−1ti−1⋅(1−t)n−i−nCn−1i(1−t)n−i−1⋅ti=n[Bi−1,n−1(t)−Bi,n−1(t)]
其中,
i
≥
1
i≥1
i≥1。当
i
=
0
i=0
i=0,
B
0
,
n
(
t
)
=
C
n
0
⋅
(
1
−
t
)
n
−
0
⋅
t
0
=
(
1
−
t
)
n
B_{0, n}(t)=C_{n}^{0} \cdot(1-t)^{n-0} \cdot t^{0}=(1-t)^{n}
B0,n(t)=Cn0⋅(1−t)n−0⋅t0=(1−t)n,故
B
0
,
n
′
(
t
)
=
−
n
(
1
−
t
)
n
−
1
=
−
n
B
0
,
n
−
1
B_{0, n}^{\prime}(t)=-n(1-t)^{n-1}=-nB_{0, n-1}
B0,n′(t)=−n(1−t)n−1=−nB0,n−1
则贝塞尔点求导:
p
n
′
(
t
)
=
[
∑
i
=
0
n
C
n
i
⋅
(
1
−
t
)
n
−
i
⋅
t
i
⋅
P
i
]
′
=
B
0
,
n
′
P
0
+
B
1
,
n
′
P
1
+
⋯
+
B
n
,
n
′
⋅
P
n
=
0
+
n
(
B
0
,
n
−
1
−
B
1
,
n
−
1
)
P
1
+
n
(
B
1
,
n
−
1
−
B
2
,
n
−
1
)
P
2
⋯
+
n
(
B
n
−
1
,
n
−
1
−
B
n
,
n
−
1
)
P
n
=
n
[
B
0
,
n
−
1
(
P
1
−
P
0
)
+
B
1
,
n
−
1
(
P
2
−
P
1
)
+
⋯
+
B
n
−
1
,
n
−
1
(
P
n
−
P
n
−
1
)
]
=
n
∑
i
=
1
n
B
i
−
1
,
n
−
1
(
t
)
⋅
(
P
i
−
P
i
−
1
)
\begin{array}{l} p_{n}^{\prime}(t)=\left[\sum_{i=0}^{n} C_{n}^{i} \cdot(1-t)^{n-i} \cdot t^{i} \cdot P_{i}\right]' \\ =B_{0, n}^{\prime} P_{0}+B_{1, n}^{\prime} P_{1}+\cdots+B_{n, n}^{\prime} \cdot P_{n} \\ =0+n\left(B_{0, n-1}-B_{1, n-1}\right) P_{1}+n\left(B_{1, n-1}-B_{2, n-1}\right) P_{2} \cdots+n\left(B_{n-1, n-1}-B_{n, n-1}\right) P_{n} \\ =n\left[B_{0, n-1}\left(P_{1}-P_{0}\right)+B_{1, n-1}\left(P_{2}-P_{1}\right)+\cdots+B_{n-1, n-1}\left(P_{n}-P_{n-1}\right)\right] \\ =n \sum_{i=1}^{n} B_{i-1, n-1}(t) \cdot\left(P_{i}-P_{i-1}\right) \end{array}
pn′(t)=[∑i=0nCni⋅(1−t)n−i⋅ti⋅Pi]′=B0,n′P0+B1,n′P1+⋯+Bn,n′⋅Pn=0+n(B0,n−1−B1,n−1)P1+n(B1,n−1−B2,n−1)P2⋯+n(Bn−1,n−1−Bn,n−1)Pn=n[B0,n−1(P1−P0)+B1,n−1(P2−P1)+⋯+Bn−1,n−1(Pn−Pn−1)]=n∑i=1nBi−1,n−1(t)⋅(Pi−Pi−1)
3 贝塞尔曲线性质
参考知乎大佬:曲线杂谈(二):Bezier曲线的特殊性质这篇文章
① 各项系数之和为1
② 系数对称性
③ 曲线的起始点和终点对应第一个和最后一个控制点
④ 凸包性
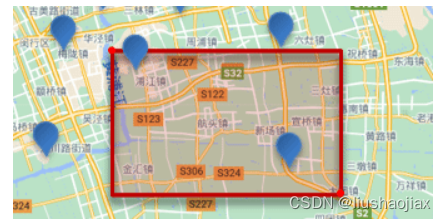
贝塞尔曲线被包含了所有控制点的最小凸多边形所包含, 这里要和控制点依次围成的最小多边形区分开。
可以通过控制点的凸包来限制规划曲线的范围
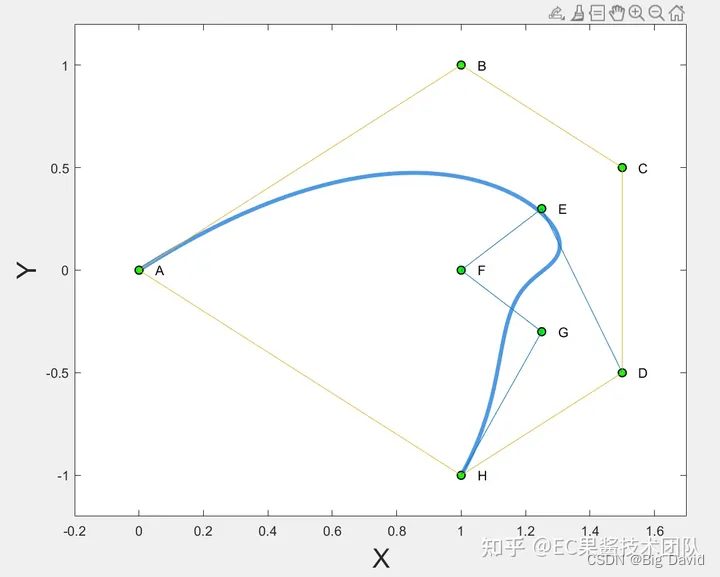 从图上可以看到,按照控制点顺序(A->B->C->D…)连接的多边形有一部分是“凹陷”的(蓝色多段线)。黄色的凸包将所有控制点(及它们之间的连线)以及贝塞尔曲线包含在内。
从图上可以看到,按照控制点顺序(A->B->C->D…)连接的多边形有一部分是“凹陷”的(蓝色多段线)。黄色的凸包将所有控制点(及它们之间的连线)以及贝塞尔曲线包含在内。
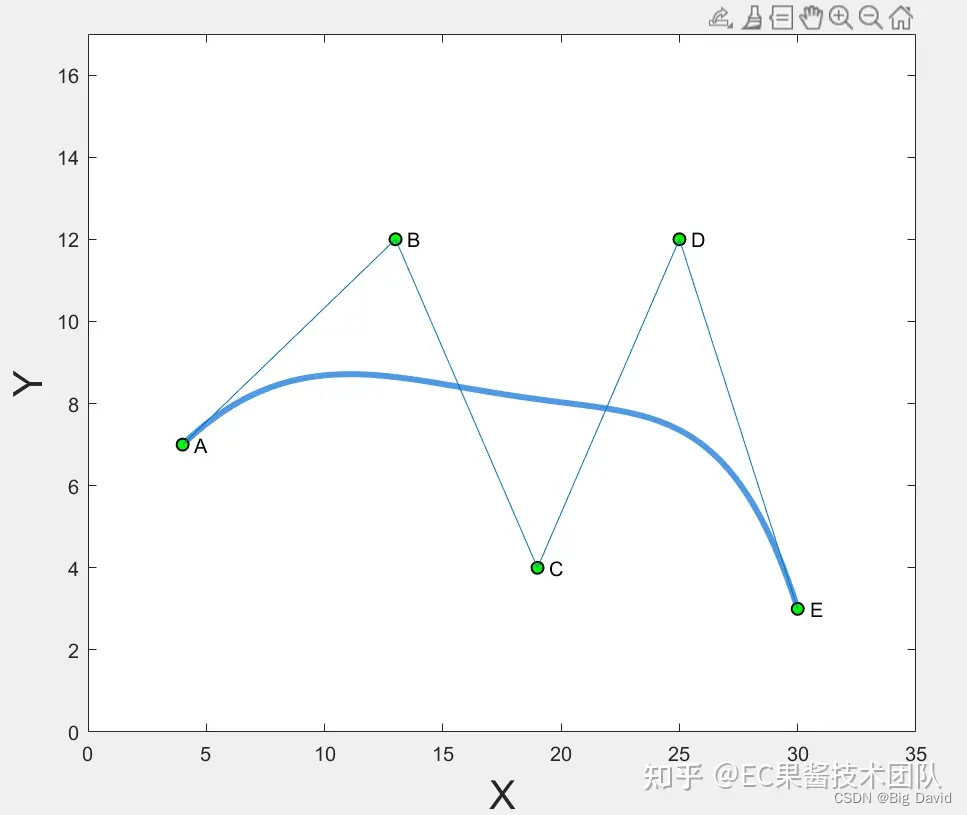
⑤ 一阶导数
贝塞尔曲线起始点和第一个控制点相切,终止点和最后一个控制点相切。可根据曲线的起始点和终止点的切线方向确定车辆起始点姿态和目标点姿态
⑥ 几何不变性
指某些几何特性不随坐标变换而变化的特性,Bezier曲线的形状仅与控制多边形各顶点的相对位置有关,而与坐标系的选择无关。
⑦ 波折递减性:控制折线比它定义的曲线复杂
⑧ 贝塞尔曲线的拼接:首尾控制点相接;连接处的四个控制点共线
若要求两端弧线拼接在一起依然是曲率连续的,必须要求两段弧线在连接处的曲率是相等的
至少需要三阶贝塞尔曲线(四个控制点)才能生成曲率连续的路径
k
=
∣
f
′
′
(
1
+
f
′
2
)
3
2
∣
k=\left|\frac{f^{\prime \prime}}{\left(1+f^{\prime 2}\right)^{\frac{3}{2}}}\right|
k=
(1+f′2)23f′′
若要求曲率连续变化,则要求至少二阶导数连续,三阶贝塞尔曲线求两次导还有变量t,是关于t连续的
(1)城市环境下局部路径规划,如贝塞尔曲线能够拟合直道和弯道,在曲率变化较大的地方可以选用两个贝塞尔曲线来拟合
(2)无人驾驶车辆的运动规划,目标轨迹曲率是连续的且轨迹的曲率不超过车辆可行驶轨迹曲率的限制
4 代码实现
MATLAB(Ally)
main1.m
clc
clear
close all
%% 直观动图感受贝塞尔曲线行程过程
% 一次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P = [P0; P1];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('一次贝塞尔曲线.gif',1);
hold on
for t = 0:0.01:1
P_t = (1-t)*P0 + t*P1;
scatter(P_t(1), P_t(2), 200, '.r');
stringName = "一次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('一次贝塞尔曲线.gif',t*100+1);
end
% 二次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P2 = [2, 1];
P = [P0; P1; P2];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('二次贝塞尔曲线.gif',1);
hold on
scatter(P(:,1), P(:,2), 200, '.b');
for t = 0:0.01:1
P_t_1 = (1-t)*P0 + t*P1;
P_t_2 = (1-t)*P1 + t*P2;
P_t_3 = (1-t)*P_t_1 + t*P_t_2;
h1 = scatter(P_t_1(1), P_t_1(2), 300, '.g');
h2 = scatter(P_t_2(1), P_t_2(2), 300, '.g');
h3 = plot([P_t_1(1), P_t_2(1)], [P_t_1(2), P_t_2(2)], 'g', 'linewidth',2);
scatter(P_t_3(1), P_t_3(2), 300, '.r');
stringName = "二次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('二次贝塞尔曲线.gif',t*100+1);
delete(h1);
delete(h2);
delete(h3);
end
% 三次贝塞尔曲线
P0 = [0, 0];
P1 = [1, 1];
P2 = [2, 1];
P3 = [3, 0];
P = [P0; P1; P2; P3];
figure;
plot(P(:,1), P(:,2), 'k');
MakeGif('三次贝塞尔曲线.gif',1);
hold on
scatter(P(:,1), P(:,2), 200, '.b');
for t = 0:0.01:1
P_t_1_1 = (1-t)*P0 + t*P1;
P_t_1_2 = (1-t)*P1 + t*P2;
P_t_1_3 = (1-t)*P2 + t*P3;
P_t_2_1 = (1-t)*P_t_1_1 + t*P_t_1_2;
P_t_2_2 = (1-t)*P_t_1_2 + t*P_t_1_3;
P_t_3 = (1-t)*P_t_2_1 + t*P_t_2_2;
h1 = scatter(P_t_1_1(1), P_t_1_1(2), 300, '.b');
h2 = scatter(P_t_1_2(1), P_t_1_2(2), 300, '.b');
h3 = scatter(P_t_1_3(1), P_t_1_3(2), 300, '.b');
h4 = plot([P_t_1_1(1); P_t_1_2(1)], [P_t_1_1(2); P_t_1_2(2)], 'b', 'linewidth',2);
h5 = plot([P_t_1_2(1); P_t_1_3(1)], [P_t_1_2(2); P_t_1_3(2)], 'b', 'linewidth',2);
h6 = scatter(P_t_2_1(1), P_t_2_1(2), 300, '.g');
h7 = scatter(P_t_2_2(1), P_t_2_2(2), 300, '.g');
h8 = plot([P_t_2_1(1); P_t_2_2(1)], [P_t_2_1(2); P_t_2_2(2)], 'g', 'linewidth',2);
scatter(P_t_3(1), P_t_3(2), 300, '.r');
stringName = "三次贝塞尔曲线:t =" + num2str(t);
title(stringName)
MakeGif('三次贝塞尔曲线.gif',t*100+1);
delete(h1);
delete(h2);
delete(h3);
delete(h4);
delete(h5);
delete(h6);
delete(h7);
delete(h8);
end
main2.m
clc
clear
close all
%%
% 定义控制点
d = 3.5;
P0 = [0, -d/2];
P1 = [25, -d/2];
P2 = [25, d/2];
P3 = [50, d/2];
P = [P0; P1; P2; P3];
% 直接根据贝塞尔曲线定义式得到路径点
n = length(P)-1;
Path = [];
for t = 0:0.01:1
if n == 1
p_t = P;
elseif n >= 2
p_t = [0, 0];
for i = 0:n
k_C = factorial(n) / (factorial(i) * factorial(n-i));
k_t = (1-t)^(n-i) * t^i;
p_t = p_t + k_C * k_t * P(i+1,:);
end
Path(end+1,:) = p_t;
else
disp('控制点输入有误,请重新输入')
end
end
%% 画图
d = 3.5; % 道路标准宽度
W = 1.8; % 汽车宽度
L = 4.7; % 车长
figure
len_line = 50;
% 画灰色路面图
GreyZone = [-5,-d-0.5; -5,d+0.5; len_line,d+0.5; len_line,-d-0.5];
fill(GreyZone(:,1),GreyZone(:,2),[0.5 0.5 0.5]);
hold on
fill([P0(1),P0(1),P0(1)-L,P0(1)-L],[-d/2-W/2,-d/2+W/2,-d/2+W/2,-d/2-W/2],'b')
% 画分界线
plot([-5, len_line],[0, 0], 'w--', 'linewidth',2); %分界线
plot([-5,len_line],[d,d],'w','linewidth',2); %左边界线
plot([-5,len_line],[-d,-d],'w','linewidth',2); %左边界线
% 设置坐标轴显示范围
axis equal
set(gca, 'XLim',[-5 len_line]);
set(gca, 'YLim',[-4 4]);
% 绘制路径
scatter(P(:,1),P(:,2),'g')
plot(P(:,1),P(:,2),'r');%路径点
scatter(Path(:,1),Path(:,2),200, '.b');%路径点
MakeGif.m
function MakeGif(filename,index)
f = getframe(gcf);
imind = frame2im(f);
[imind,cm] = rgb2ind(imind,256);
if index==1
imwrite(imind,cm,filename,'gif', 'Loopcount',inf,'DelayTime',0.001);
else
imwrite(imind,cm,filename,'gif','WriteMode','append','DelayTime',0.001);
end
end
C++:
BezierCurve.h
#pragma once
#include <iostream>
#include <Eigen/Dense>
#include <vector>
#include <cmath>
#include <algorithm>
using namespace std;
using namespace Eigen;
double factorial(int n);
Vector2d bezierCommon(vector<Vector2d>& Ps, double t);
BezierCurve.cpp
#include "BezierCurve.h"
// 阶乘实现
double factorial(int n) {
if (n <= 1) return 1;
return factorial(n - 1) * n;
}
// 贝塞尔
Vector2d bezierCommon(vector<Vector2d>& Ps, double t) {
if(Ps.size() == 1) return Ps[0];
Vector2d p_t(0, 0);
int n = Ps.size()-1;
for(int i = 0; i < Ps.size(); i++){
double C_n_i = factorial(n) / (factorial(i) * factorial(n-i));
p_t += C_n_i * pow((1-t),(n-i)) * pow(t,i) * Ps[i];
}
return p_t;
}
main.cpp
#include "BezierCurve.h"
#include "matplotlibcpp.h"
namespace plt = matplotlibcpp;
int main(int argc, char** argv) {
// 四阶贝塞尔
vector<Vector2d> Ps{Vector2d(0,0), Vector2d(1,1), Vector2d(2,1), Vector2d(3,0), Vector2d(4,2)};
/*// 三阶
vector<Vector2d> Ps{Vector2d(0,0), Vector2d(1,1), Vector2d(2,1), Vector2d(3,0)};
// 二阶
vector<Vector2d> Ps{Vector2d(0,0), Vector2d(1,1), Vector2d(2,1)};
// 一阶
vector<Vector2d> Ps{Vector2d(0,0), Vector2d(1,1)};*/
vector<double> x_ref, y_ref;
for(int i = 0; i < Ps.size(); i++){
x_ref.push_back(Ps[i][0]);
y_ref.push_back(Ps[i][1]);
}
vector<double> x_, y_;
for (int t = 0; t < 100; t++) {
plt::clf();
Vector2d pos = bezierCommon(Ps, (double)t/100);
x_.push_back(pos[0]);
y_.push_back(pos[1]);
plt::plot(x_, y_, "r");
plt::plot(x_ref, y_ref);
plt::pause(0.01);
}
// save figure
const char* filename = "./bezier_demo.png";
plt::save(filename);
plt::show();
return 0;
}
运行结果:
四阶贝塞尔
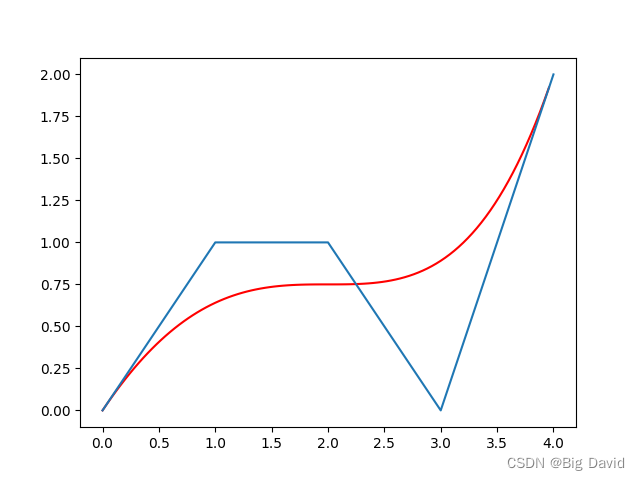 三阶贝塞尔
三阶贝塞尔
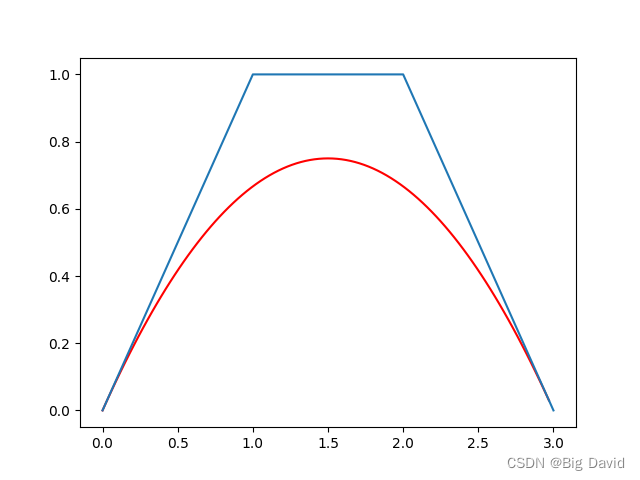 二阶贝塞尔
二阶贝塞尔
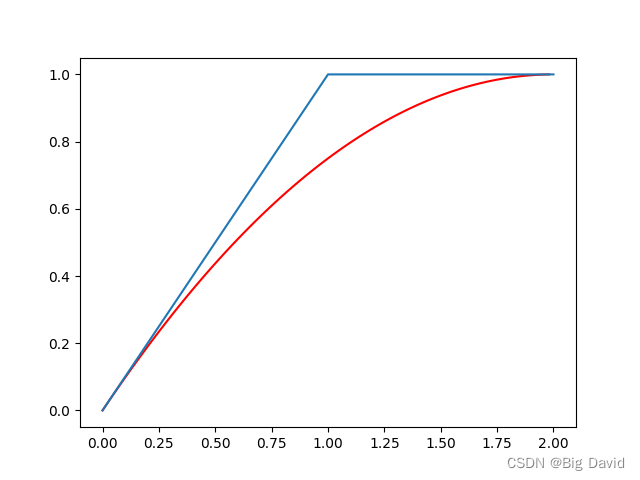 一阶贝塞尔
一阶贝塞尔

贝塞尔讲解正式结束,不正之处望读者指出