20240316-1-向量化搜索

向量化搜索

在高维空间内快速搜索最近邻（Approximate Nearest Neighbor）。召回中，Embedding向量的搜索。

FAISS、kd-tree、局部敏感哈希、【Amnoy、HNSW】

FAISS

faiss是Facebook的AI团队开源的一套用于做聚类或者相似性搜索的软件库，底层是用C++实现。Faiss因为超级优越的性能，被广泛应用于推荐相关的业务当中。

faiss工具包一般使用在推荐系统中的向量召回部分。在做向量召回的时候要么是u2u，u2i或者i2i，这里的u和i指的是user和item。我们知道在实际的场景中user和item的数量都是海量的，最容易想到的基于向量相似度的召回就是使用两层循环遍历user列表或者item列表计算两个向量的相似度，但是这样做在面对海量数据是不切实际的，faiss就是用来加速计算某个查询向量最相似的topk个索引向量。

faiss查询的原理：

faiss使用了PCA和PQ(Product quantization乘积量化)两种技术进行向量压缩和编码，当然还使用了其他的技术进行优化，但是PCA和PQ是其中最核心部分。

主要流程

构建索引index
根据不同索引的特性，对索引进行训练（train）
add 添加xb数据到索引
针对xq进行搜索search操作

Example

1、数据集

d = 64                           # dimension
nb = 100000                      # 完整数据集
nq = 10000                       # 查询数据
np.random.seed(1234)             
xb = np.random.random((nb, d)).astype('float32')
xb[:, 0] += np.arange(nb) / 1000.
xq = np.random.random((nq, d)).astype('float32')
xq[:, 0] += np.arange(nq) / 1000.

2、构建索引

Faiss围绕Index对象构建。它封装了数据库向量集，并可选地对其进行预处理以提高搜索效率。索引的类型很多，我们将使用最简单的索引，它们仅对它们执行暴力L2距离搜索：IndexFlatL2。

d在我们的例子中，所有索引都需要知道何时建立索引，即它们所操作的向量的维数

index = faiss.IndexFlatL2(d)   # build the index

3、对索引进行训练

然后，大多数索引还需要训练阶段，以分析向量的分布。对于IndexFlatL2，我们可以跳过此操作。

4、添加数据到索引

构建和训练索引后，可以对索引执行两项操作：add和search。

将元素添加到索引，我们称之为add上xb。我们还可以显示索引的两个状态变量：is_trained，指示是否需要训练的布尔值，以及ntotal索引向量的数量。

一些索引还可以存储与每个向量相对应的整数ID（但不能存储IndexFlatL2）。如果未提供ID，则add只需将向量序号用作ID，即。第一个向量为0，第二个为1，依此类推。

index.add(xb)                  # add vectors to the index

5、对查询数据进行搜索操作

可以对索引执行的基本搜索操作是k-最近邻搜索，即。对于每个查询向量，k在数据库中找到其最近的邻居。

该操作的结果可以方便地存储在一个大小为nq-by-的整数矩阵中k，其中第i行包含查询向量i的邻居ID（按距离递增排序）。除此矩阵外，该search操作还返回一个具有相应平方距离的nq按k浮点矩阵。

k = 4                          # we want to see 4 nearest neighbors
D, I = index.search(xb[:5], k) # sanity check, 首先搜索一些数据库向量，以确保最近的邻居确实是向量本身
print(I)
print(D)
D, I = index.search(xq, k)     # actual search
print(I[:5])                   # neighbors of the 5 first queries
print(I[-5:])                  # neighbors of the 5 last queries

索引方式

Faiss中的稠密向量各种索引都是基于 Index实现的，主要的索引方法包括： IndexFlatL2、IndexFlatIP、IndexHNSWFlat、IndexIVFFlat、IndexLSH、IndexScalarQuantizer、IndexPQ、IndexIVFScalarQuantizer、IndexIVFPQ、IndexIVFPQR等，每个方法的具体介绍。

IndexFlatL2：

基于L2距离的暴力全量搜索，速度较慢，不需要训练过程。

IndexIVFFlat：

先聚类再搜索，可以加快检索速度；
先将xb中的数据进行聚类（聚类的数目是超参），nlist: 聚类的数目
nprobe: 在多少个聚类中进行搜索，默认为1, nprobe越大，结果越精确，但是速度越慢

def IndexIVFFlat(nlist):
    quantizer = faiss.IndexFlatL2(d)
    index = faiss.IndexIVFFlat(quantizer, d, nlist)
    print(index.is_trained)
    index.train(xb)
    print(index.is_trained)
    index.add(xb)
    return index

IndexIFVPQ

基于乘积量化（product quantizers）对存储向量进行压缩，节省存储空间
m：乘积量化中，将原来的向量维度平均分成多少份，d必须为m的整数倍
bits: 每个子向量用多少个bits表示

def IndexIVFPQ(nlist, m, bits):
    quantizer = faiss.IndexFlatL2(d)
    index = faiss.IndexIVFPQ(quantizer, d, nlist, m, bits)
    index.train(xb)
    index.add(xb)
    return index

kd树

kd树是一种对k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构。kd树是二叉树，表示对k维空间的一个划分（partition）。构造kd树相当于不断地用垂直于坐标轴的超平面将k维空间切分，构成一系列的k维超矩形区域。kd树的每个结点对应于一个k维超矩形区域。

kd树的结构

kd树是一个二叉树结构，它的每一个节点记载了【特征坐标，切分轴，指向左枝的指针，指向右枝的指针】。

其中，特征坐标是线性空间 $\mathbf{R}^n$ 的一个点 $x_1,...,x_n)$ 。

切分轴由一个整数 $r$ 表示，这里 $1\leq r\leq n$ ，是我们在 $n$ 维空间中沿第 $n$ 维进行一次分割。

节点的左枝和右枝分别都是 kd 树，并且满足：如果 y 是左枝的一个特征坐标，那么 $y_r \leq x_r$ 并且如果 z 是右枝的一个特征坐标，那么$x_r \leq z_r $。

kd树的构造

通过数据集来构造kd树存储空间，在推荐系统中即用物品Embedding池进行构建。

输入：k维空间数据集 $T=\left\{x_{1}, x_{2}, \cdots, x_{N}\right\}$ ，其中 $x_{i}=\left(x_{i}^{(1)}, x_{i}^{(2)}, \cdots, x_{i}^{(k)}\right)^{\mathrm{T}},i=1,2,...,N$ ；
输出：kd树；
（1）开始：构造根结点，根结点对应于包含 $T$ 的 $k$ 维空间的超矩形区域。

选择 $x^{(1)}$ 为坐标轴，以 $T$ 中所有实例的 $x^{(1)}$ 坐标的中位数为切分点【若超平面上没有切分点，可以适当移动位置，使得超平面上有点】，将根结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^{(1)}$ 垂直的超平面实现。

由根结点生成深度为1的左、右子结点：左子结点对应坐标 $x^{(1)}$ 小于切分点的子区域，右子结点对应于坐标 $x^{(1)}$ 大于切分点的子区域。
将落在切分超平面上的实例点保存在根结点。
（2）重复：对深度为 $j$ 的结点，选择 $x^{(l)}$ 为切分的坐标轴， $l=j(\bmod k)+1$ ，以该结点的区域中所有实例的 $x^{(l)}$ 坐标的中位数为切分点，将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 $x^{(l)}$ 垂直的超平面实现。
由该结点生成深度为 $j + 1$ 的左、右子结点：左子结点对应坐标 $x^{(l)}$ 小于切分点的子区域，右子结点对应坐标 $x^{(l)}$ 大于切分点的子区域
将落在切分超平面上的实例点保存在该结点。
（3）直到两个子区域没有实例存在时停止。从而形成kd树的区域划分。

最后每一部分都只剩一个点，将他们记在最底部的节点中。因为不再有未被记录的点，所以不再进行切分。

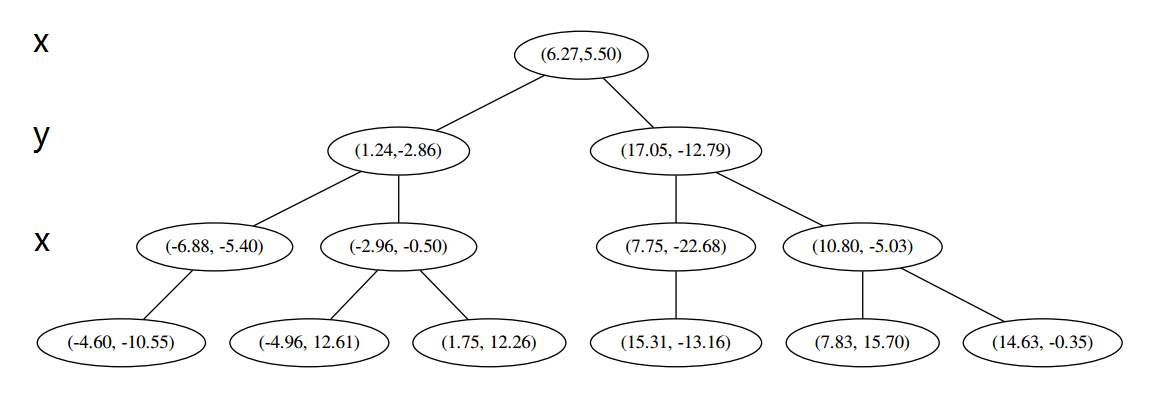
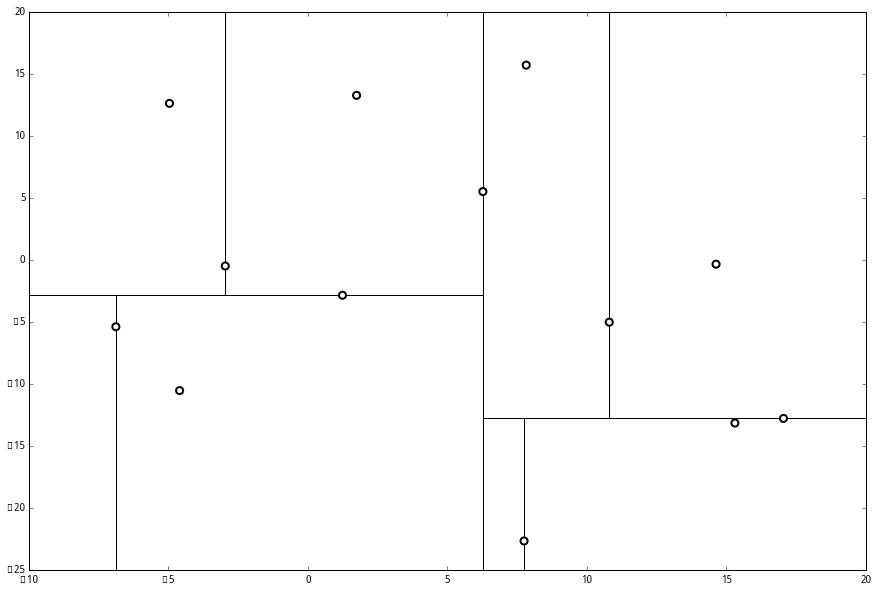
搜索kd树

在推荐系统中，即通过用户的Embedding向量来查找与其近邻的 $K$ 个物品Embedding向量。

输入：已构造的kd树；目标点 $x$ ；
输出： $x$ 的 $k$ 近邻；
设有一个$ k$个空位的列表，用于保存已搜寻到的最近点。
（1）在kd树中找出包含目标点 $x$ 的叶结点：从根结点出发，递归地向下访问树。若目标点 $x$ 当前维的坐标小于切分点的坐标，则移动到左子结点，否则移动到右子结点，直到子结点为叶结点为止；
（2）如果**“当前k近邻点集”元素数量小于 $k$ 或者叶节点距离小于“当前k近邻点集”中最远点距离**，那么将叶节点插入“当前k近邻点集”；
（3）递归地向上回退，在每个结点进行以下操作：
- 如果“当前k近邻点集”元素数量小于k或者当前节点距离小于“当前k近邻点集”中最远点距离，那么将该节点插入“当前k近邻点集”。
- 检查该子结点的父结点的另一子结点对应的区域是否与以目标点为球心、以目标点与于“当前k近邻点集”中最远点间的距离为半径的超球体相交。如果相交，可能在另一个子结点对应的区域内存在距目标点更近的点，移动到另一个子结点，接着，递归地进行最近邻搜索；如果不相交，向上回退；
当回退到根结点时，搜索结束，最后的“当前k近邻点集”即为 $x$ 的k近邻点。

kd树的平均计算复杂度是 $l o g (N)$ 。

参考资料：kd 树算法之详细篇

局部敏感哈希

局部敏感哈希的基本思想：

让相邻对的点落入同一个“桶”，这样在进行最近邻搜索时，仅需要在一个桶内，或相邻的几个桶内的元素中进行搜索即可。如果保持每个桶中的元素个数在一个常数附近，就可以把最近邻搜索的时间复杂度降低到常数级别。

首先需要明确一个概念，

在欧式空间中，将高维空间的点映射到低维空间，原本相近的点在低维空间中肯定依然相近，但原本远离的点则有一定概率变成相近的点。

所以利用低维空间可以保留高维空间相近距离关系的性质，就可以构造局部敏感哈希的桶。

对于Embedding向量，可以用内积操作构建局部敏感哈希桶。假设 $\mathbf{v}$ 是高维空间中的 $k$ 维Embedding向量， $\mathbf{x}$ 是随机生成的 $k$ 维向量。内积操作可以将 $\mathbf{v}$ 映射到1维空间，成为一个数值：
$h(\mathbf{v})=\mathbf{v}\cdot \mathbf{x}$
因此，可以使用哈希函数 $h (v)$ 进行分桶：
$h^{x,b}(\mathbf{v})=\lfloor x \frac{\mathbf{x}\cdot \mathbf{v}+ b}{w}\rfloor x$
其中 $\lfloor \rfloor$ 是向下取整， $w$ 是分桶宽度， $b$ 是0到 $w$ 间的一个均匀分布随机变量，避免分桶边界固化。