文章目录
- 前言
- 46.数据结构介绍
- 47.列表
- 48.栈的介绍
- 49.栈的应用:括号匹配问题
- 50.队列的介绍
- 51.队列的实现
- 52.队列的内置模块
- 总结
前言
学习python数据结构与算法,学习常用的算法,
b站学习链接
46.数据结构介绍
- 数据结构是指相互之间存在着一种或多种关系的数据元素的集合和该结婚钟数据元素之间的关系组成。
- 简单来说,数据结构就是设计数据以何种方式组织并存储在计算机中。
- 比如:列表、集合于字典等都是一种数据结构。
- 程序= 数据结构+算法
数据结构按照其逻辑结构可分为线性结构、树结构、图结构
线性结构:数据结构的元素存在一对一的相互关系
树结构:数据结构中的元素存在一对多的相互关系
图结构:数据结构中的元素存在多对多的相互关系
图结构就相当于地图 去一个地方可以有好几条路径,也可以是一个地方可以去好几个地方。
47.列表
列表(其他语言称是数组)是一种基本数据类型
先讲一下C语言的数组是怎么实现存储的。
先开一个数组int a[7],代表开辟存7个整型的空间

比方说第0个位置存1,这个地址是100,
在32位的机器上,一个整数占4个字节(32/8=4)一个字节8位。
(补充:32位的机器最大内存就是4G,因为一共能存储2^32-1=4,294,967,295个bit,是4g=4,294,967,296)
所以第1个位置的地址是104,这里存2,第2个位置是108,存3
那么我查找这个元素是a[2],底层的实现是先找到这个地址100+2*4=108,再从这个位置取出3这个值,所需要的时间复杂度是O(1)
数组和列表有两点不同:
1.数组元素类型要相同
2.数组长度固定。
再说一下python中的列表是如何实现存储的,首先开一个列表[],C语言需要指定它的数组长度而python不需要,可以无限append。(list.append()在列表后追加一个元素)
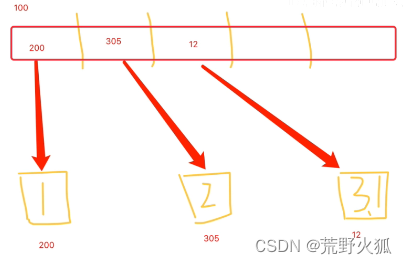
而列表里面元素类型可以不相同,因为列表里存的元素是地址,比方说把1存在地址200这个格子里,再把地址200存在列表第0个位置里,2存在地址305里,再把305存在列表第1个位置里。这样列表里的元素就可以是整型,浮点型,不同的元素类型了,1占用200-203,3.1占用12-19,就可以分别占用地址了。
最后列表比方说还是从地址100开始,那么我们取list[2]这个元素时,就可以和C一样,100+2*4,因为i地址都是整型存储了,所以可以找到108的位置是12,这里就比C多了一步,C到这就可以取出3来,而python还要从12这个地址再取出3.1来,存储上是C花销的两倍。
所以python列表的查找操作的时间复杂度是O(1)
删除和插入操作的复杂度呢,在第0个位置删除1,我们需要把它后面的元素全往前一个位置,所以是O(n)。插入也是一样,先把这个位置的后面的元素往后挪一个元素,再插入,时间复杂度也是O(n)
补充:Python垃圾回收机制之小整数对象池
python里的 假设1存在200,2存在305,3存在12 (python内部解释器已经建好了一个固定的小整数池)
a=1 #a指到200的位置
b=1 #b指到200的位置
b=3 #b重新指到12的位置
48.栈的介绍
栈就相当于一叠便利贴,只支持你把便利贴贴上去,或者完成后,把便利贴取下来。
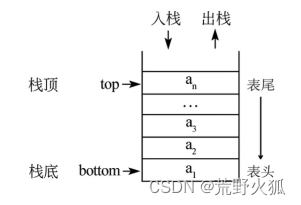
栈(Stack)是一个数据集合,可以理解为智能在一端进行插入或者删除操作的列表。
栈的特点:后进先出LIFO(last-in,first-out)
栈的概念:栈顶、栈底
栈的基本操作:
进栈(压栈):push
出栈:pop
取栈顶:gettop (只是看一下栈顶是什么,不把它丢掉。)
栈实现:一般使用列表结构就能实现
进栈:li.append
出栈:li.pop
取栈顶:li[-1]

49.栈的应用:括号匹配问题
括号匹配问题:给一个字符串,其中包含小括号、中括号、大括号,求该字符中的括号是否匹配
例如:
()()[]{} 匹配
({{[]}})匹配
[]( 不匹配
{(})
思路:
用栈的思想,一个一个遍历字符,如果是左边的括号,就进栈,如果栈顶和遍历的字符匹配,就出栈。最后当栈内没有元素就说明括号是匹配的,否则不匹配。
50.队列的介绍
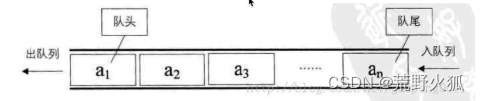
队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。
进行插入的一端称为队尾(rear),插入动作称为进队或者入队
进行删除的一端称为队头(front),删除动作称为出队
队列的性质:先进先出(First-in,First-out)
就可以看作成现实生活中的排队
尝试用列表简单建立队列,发现列表的出队pop是O(n)的复杂度,会将队伍往前挪一个位置,入队append是在队尾再加一个元素,rear指针往后挪一个位置。实现起来复杂度太高了。
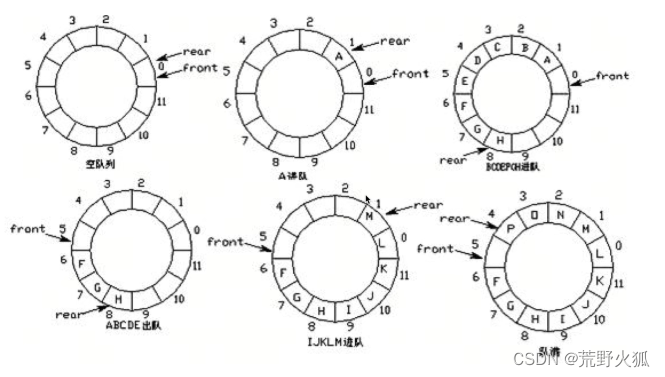
可以用环形队列的实现方式。
环形队列:当队尾或者队首指针 ==MaxSize -1时,再前进一个位置时,就自动到0
队空时:rear == front
进队时:队尾指针前进1 :rear = (rear + 1)%MaxSize 这里就是12
出队时:队首指针前进1:front = (front+1) %MaxSize (取余的操作刚好构成了一个环形)
队满时:(rear+1)%MaxSize ==front (因为如果不空一个,就会使得rear == front 无法判断队空还是队满,当rear为11,front=0时,real+1 不等于front,但是达到了队满,所以加上%MaxSize)
51.队列的实现
队列创建列表,大小为5,当4个有值时说明满了。

有0 1 2 3 4 五个位置,front和rear首先都指向0,先入队0,1,2,3 四个值,入队时,先将rear指向1,在1这个位置存0,然后2位置存1 ,3位置存2 ,4位置存3,现在本来00000,变成00123,然后出队列,把front指向位置1,返回在位置1上的值,是0。

虽然位置0上还有值,但是我们已经不care它是多少了,它会被后来的入队给覆盖掉,就相当于是删除了。最后在队列为空时不能出队,队列为满时不能入队做一个边界判断。
52.队列的内置模块
使用方法:from collections import deque
双向队列:(两边都可以进队,出队)
创建队列: queue= deque()
进队:append()
出队:popleft()
双向队列队首进队:qppendleft()
双向队列队尾出队:pop()
内置的队列,有个特点,当队满时,踢出第一个,所以这里入队了6,保持队伍长度为5,[2,3,4,5,6],再popleft时,就是2出队
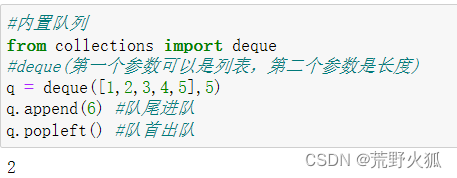
然后队首进队1,队尾出6,队列为deque([1, 3, 4, 5])

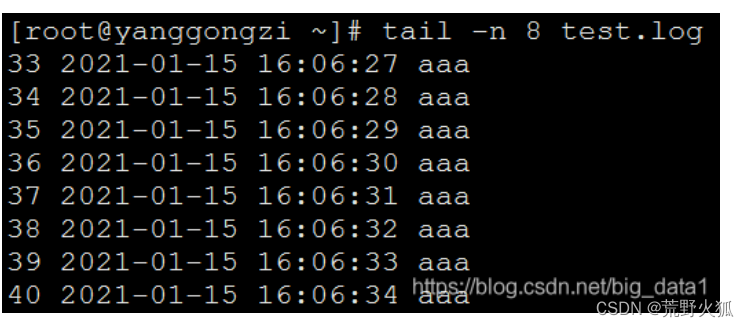
用队列来实现linux的tail命令,tail -n 8 ,就是打印文件的后8行。借用一下别人的图。
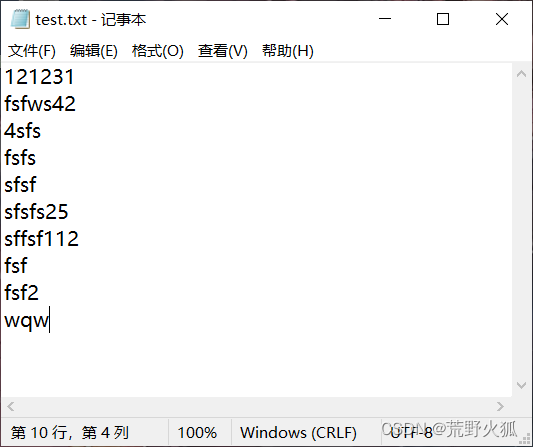
先随便写10行,名叫test.txt,放在.py的同目录下。
 yuan
yuan
原理和刚刚一样,队满时,踢出第一个,将最后一个放入,保持队列为5个元素,所以最后就是后5个元素。

打印一下,因为python打印会自动换行,不让它自动换行,加end=“”

总结
学习了基础的数据结构,列表,栈,队列。
文章目录
- 前言
- 46.数据结构介绍
- 47.列表
- 48.栈的介绍
- 49.栈的应用:括号匹配问题
- 50.队列的介绍
- 51.队列的实现
- 52.队列的内置模块
- 总结

![快速搭建ChatGPT的AI聊天QQ机器人[含问题解决办法]](https://img-blog.csdnimg.cn/1d4fc2ce693c4c63a29ff2309e95e7a5.png)


![P2010 [NOIP2016 普及组] 回文日期————C++](https://img-blog.csdnimg.cn/9b8396dc072b42bea58220973b89dea8.png)