目录
- 前言
- 一、Lagrange(拉格朗日)插值
- 1. 线性插值
- 2. 抛物插值
- 3. 拉格朗日插值多项式
- 二、Lagrange插值算法及matlab代码
- 1. Lagrange 插值算法matlab实现
- 2 实例
- 3. 线性插值示意图代码
- 4. 抛物插值示意图代码
- 三、总结
- 四、插值法专栏
前言
本篇为插值法专栏第三篇内容讲述,此章主要讲述 Lagrange(拉格朗日)插值法及matlab代码,其中也给出详细的例子让大家更好的理解Lagrange插值法
提示 之前已经介绍牛顿插值法和三次样条插值,如果没看过前两篇的可以点击以下链接阅读
- 数值分析(一)牛顿插值法
- 数值分析(二)三次样条插值法
- 数值分析(二续) 三次样条插值二类边界完整matlab代码
- 数值分析(三) Lagrange(拉格朗日)插值法及Matlab代码实现
- 数值分析(四) Hermite(埃尔米特)插值法及matlab代码
一、Lagrange(拉格朗日)插值
为了构造满足插值条件 p ( x i ) = f ( x i ) , ( i = 0 , 1 , 2 , … , n ) p(x_i) = f(x_i), (i=0, 1, 2, \dots, n) p(xi)=f(xi),(i=0,1,2,…,n)的便于使用的插值多项式 P ( x ) P(x) P(x) ,在介绍Lagrange插值前先补充一下 线性插值 和 抛物插值 的知识点。
1. 线性插值
线性插值是代数插值的最简单形式。假设给定了函数
f
(
x
)
f(x)
f(x) 在两个互异的点的值,
x
0
,
x
1
,
y
0
=
f
(
x
0
)
,
y
1
=
f
(
x
1
)
x_0, x_1, y_0 = f(x_0), y_1 = f(x_1)
x0,x1,y0=f(x0),y1=f(x1) ,现要求用线性函数
p
(
x
)
=
a
x
+
b
p(x) = ax+b
p(x)=ax+b 近似的代替
f
(
x
)
f(x)
f(x)。选择参数
a
a
a 和
b
b
b, 使
p
(
x
i
)
=
f
(
x
i
)
,
(
i
=
0
,
1
)
p(x_i) = f(x_i), (i=0, 1)
p(xi)=f(xi),(i=0,1)。称这样的线性函数
P
(
x
)
P(x)
P(x) 为
f
(
x
)
f(x)
f(x) 的线性插值函数。
线性插值的几何意义:用通过点
A
(
x
0
,
f
(
x
0
)
)
A(x_0, f(x_0))
A(x0,f(x0)) 和
B
(
x
1
,
f
(
x
1
)
)
B(x_1, f(x_1))
B(x1,f(x1)) 的直线近似地代替曲线
y
=
f
(
x
)
y=f(x)
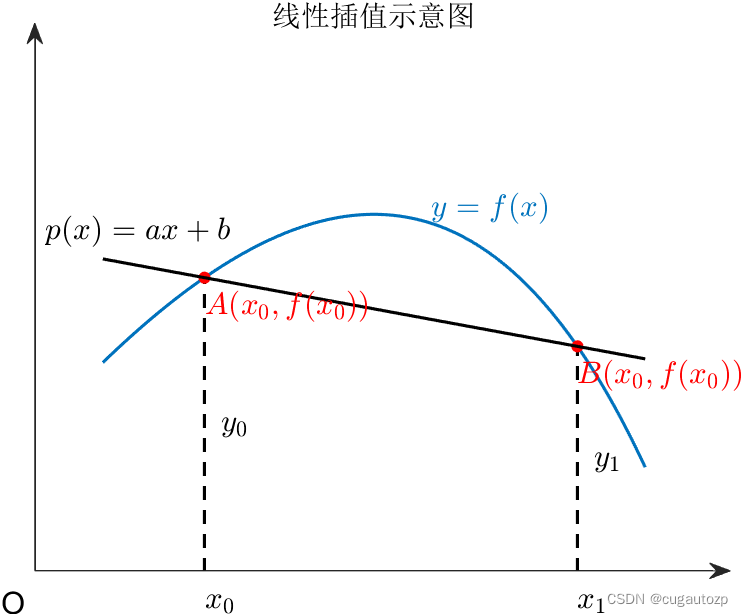
y=f(x) 由解析几何知道,这条直线用点斜式表示为(如下图所示):
p
(
x
)
=
y
0
+
y
1
−
y
0
x
1
−
x
0
(
x
−
x
0
)
→
p
(
x
)
=
x
−
x
1
x
0
−
x
1
y
0
+
x
−
x
0
x
1
−
x
0
y
1
p(x) = {y_0} + \frac{{{y_1} - {y_0}}}{{{x_1} - {x_0}}}(x - {x_0}) \to p(x) = \frac{{x - {x_1}}}{{{x_0} - {x_1}}}{y_0} + \frac{{x - {x_0}}}{{{x_1} - {x_0}}}{y_1}
p(x)=y0+x1−x0y1−y0(x−x0)→p(x)=x0−x1x−x1y0+x1−x0x−x0y1
为了便于推广,那么记
l
0
(
x
)
=
x
−
x
1
x
0
−
x
1
,
l
1
(
x
)
=
x
−
x
0
x
1
−
x
0
l_0(x) = \frac{x-x_1}{x_0-x_1}, l_1(x) = \frac{x-x_0}{x_1-x_0}
l0(x)=x0−x1x−x1,l1(x)=x1−x0x−x0这是一次函数,具有如下性质
l
0
(
x
0
)
=
1
,
l
0
(
x
1
)
=
0
,
l
1
(
x
0
)
=
0
l
1
(
x
1
)
=
1
l
0
(
x
)
+
l
1
(
x
)
=
1
\begin{matrix} l_0(x_0)=1, & l_0(x_1)=0, \\ l_1(x_0) = 0 & l_1(x_1) = 1\end{matrix} \\ l_0(x)+l_1(x) =1
l0(x0)=1,l1(x0)=0l0(x1)=0,l1(x1)=1l0(x)+l1(x)=1
那么可以记为:
l
k
(
x
i
)
=
δ
k
i
=
{
1
(
i
=
k
)
0
(
i
≠
k
)
l_k(x_i) = \delta_{ki}= \left\{\begin{matrix} 1 & (i=k)\\0 &(i \ne k) &\end{matrix}\right.
lk(xi)=δki={10(i=k)(i=k)那么
l
0
(
x
)
l_0(x)
l0(x) 和
l
1
(
x
)
l_1(x)
l1(x) 称为线性插值基函数,且有
l
k
(
x
)
=
∏
j
=
0
,
j
≠
k
1
x
−
x
j
x
k
−
x
j
,
(
k
=
0
,
1
)
l_k(x) = \prod_{j=0,j \ne k}^{1}\frac{x-x_j}{x_k-x_j}, (k=0,1)
lk(x)=j=0,j=k∏1xk−xjx−xj,(k=0,1) 则上述线性插值函数可以表示为与基函数的线性组合
p
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
p(x) = l_0(x)y_0 + l_1(x)y_1
p(x)=l0(x)y0+l1(x)y1
2. 抛物插值
抛物插值又称二次插值,它也是常用的代数插值之一。设已知
f
(
x
)
f(x)
f(x) 在三个互异点
x
0
,
x
1
,
x
2
x_0, x_1, x_2
x0,x1,x2的函数值
y
0
,
y
1
,
y
2
y_0, y_1, y_2
y0,y1,y2,要构造次数不超过二次的多项式
P
(
x
)
=
a
2
x
2
+
a
1
x
+
a
0
P(x) = a_2x^2 + a_1x + a_0
P(x)=a2x2+a1x+a0 使满足二次插值条件:
P
(
x
i
)
=
y
i
(
i
=
0
,
1
,
2
)
P(x_i) = y_i (i=0,1,2)
P(xi)=yi(i=0,1,2) 这就是二次插值问题。其几何意义是用经过3个点
(
x
0
,
y
0
)
,
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
(x{}_0,{y_0}),(x{}_1,{y_1}),(x{}_2,{y_2})
(x0,y0),(x1,y1),(x2,y2) 的抛物线
y
=
P
(
x
)
y=P(x)
y=P(x) 近似代替曲线
y
=
f
(
x
)
y = f(x)
y=f(x) , 如下图所示。因此也称之为抛物插值。
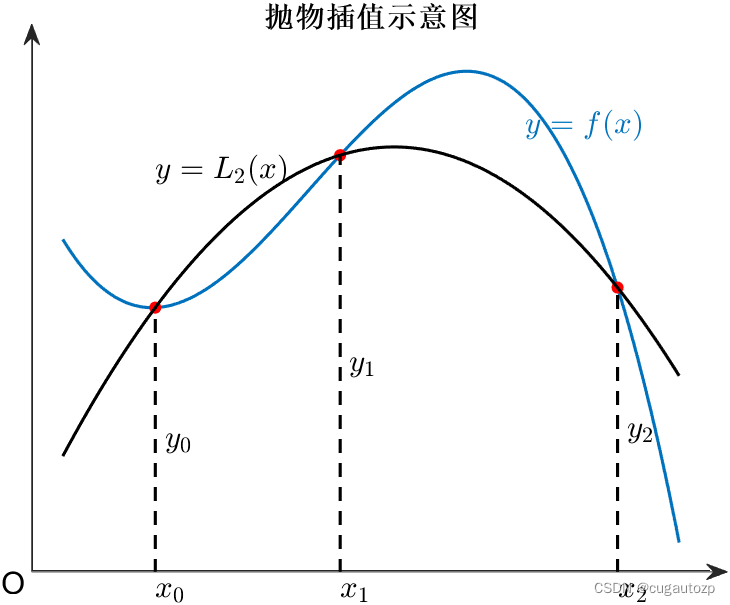
线性插值 和 抛物插值 两个示意图使用matlab绘制,并借助使用了 slandarer 大佬的一个绘制带箭头的坐标轴工具箱,代码将在下方给出
其中 P ( x ) P(x) P(x) 的参数 a 0 , a 1 , a 2 a_0,a_1,a_2 a0,a1,a2 直接由插值条件决定,即 a 0 , a 1 , a 2 a_0,a_1,a_2 a0,a1,a2 满足下面的代数方程组: { a 0 + a 1 x 0 + a 2 x 0 2 = y 0 a 0 + a 1 x 1 + a 2 x 1 2 = y 1 a 0 + a 1 x 2 + a 2 x 2 2 = y 2 \left\{ \begin{array}{l} {a_0} + {a_1}{x_0} + {a_2}x_0^2 = {y_0}\\ {a_0} + {a_1}{x_1} + {a_2}x_1^2 = {y_1}\\ {a_0} + {a_1}{x_2} + {a_2}x_2^2 = {y_2} \end{array} \right. ⎩ ⎨ ⎧a0+a1x0+a2x02=y0a0+a1x1+a2x12=y1a0+a1x2+a2x22=y2 那么其系数矩阵为: [ 1 x 0 x 0 2 1 x 1 x 1 2 1 x 2 x 2 2 ] \left[ {\begin{matrix} 1&{{x_0}}&{x_0^2}\\ 1&{{x_1}}&{x_1^2}\\ 1&{{x_2}}&{x_2^2} \end{matrix}} \right] 111x0x1x2x02x12x22 此行列式是范德蒙行列式,当 x 0 ≠ x 1 ≠ x 2 x_0 \ne x_1 \ne x_2 x0=x1=x2 时,方程组的解唯一,为了与下一节的Lagrange插值公式比较,仿线性插值,用基函数的方法求解方程组,求二次式 l 0 ( x ) l_0(x) l0(x),使其满足条件: l 0 ( x 0 ) = 1 , l 0 ( x 1 ) = 0 , l 0 ( x 2 ) = 0 l_0(x_0)=1, l_0(x_1)=0,l_0(x_2)=0 l0(x0)=1,l0(x1)=0,l0(x2)=0,于是可以知道 x 1 , x 2 x_1,x_2 x1,x2是 l 0 ( x ) l_0(x) l0(x) 的两个零点,则 l 0 ( x ) = c ( x − x 1 ) ( x − x 2 ) {l_0}(x) = c(x - {x_1})(x - {x_2}) l0(x)=c(x−x1)(x−x2)再由另一个条件 l 0 ( x 0 ) = 1 l_0(x_0)=1 l0(x0)=1解得系数为 c = 1 ( x 0 − x 1 ) ( x 0 − x 2 ) c = \frac{1}{{({x_0} - {x_1})({x_0} - {x_2})}} c=(x0−x1)(x0−x2)1从而导出 l 0 ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) {l_0}(x) = \frac{{(x - {x_1})(x - {x_2})}}{{({x_0} - {x_1})({x_0} - {x_2})}} l0(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)类似地可以构造出满足条件: l 0 ( x 0 ) = 0 , l 0 ( x 1 ) = 1 , l 0 ( x 2 ) = 0 l_0(x_0)=0, l_0(x_1)=1,l_0(x_2)=0 l0(x0)=0,l0(x1)=1,l0(x2)=0的插值多项式 l 1 ( x ) = ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) {l_1}(x) = \frac{{(x - {x_0})(x - {x_2})}}{{({x_1} - {x_0})({x_1} - {x_2})}} l1(x)=(x1−x0)(x1−x2)(x−x0)(x−x2)以及满足条件 l 0 ( x 0 ) = 0 , l 0 ( x 1 ) = 0 , l 0 ( x 2 ) = 1 l_0(x_0)=0, l_0(x_1)=0,l_0(x_2)=1 l0(x0)=0,l0(x1)=0,l0(x2)=1 的插值多项式 l 2 ( x ) = ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) {l_2}(x) = \frac{{(x - {x_0})(x - {x_1})}}{{({x_2} - {x_0})({x_2} - {x_1})}} l2(x)=(x2−x0)(x2−x1)(x−x0)(x−x1)这样构造出来的 l 0 ( x ) , l 0 ( x ) , l 0 ( x ) l_0(x), l_0(x),l_0(x) l0(x),l0(x),l0(x)称为抛物插值的基函数,取已知数据 y 0 , y 1 , y 2 {y_0},{y_1},{y_2} y0,y1,y2 作为线性组合系数,将基函数 l 0 ( x ) , l 1 ( x ) , l 2 ( x ) {l_0}(x),{l_1}(x),{l_2}(x) l0(x),l1(x),l2(x)线性组合可得 P ( x ) = ( x − x 1 ) ( x − x 2 ) ( x 0 − x 1 ) ( x 0 − x 2 ) y 0 + ( x − x 0 ) ( x − x 2 ) ( x 1 − x 0 ) ( x 1 − x 2 ) y 1 + ( x − x 0 ) ( x − x 1 ) ( x 2 − x 0 ) ( x 2 − x 1 ) y 2 P(x) = \frac{{(x - {x_1})(x - {x_2})}}{{({x_0} - {x_1})({x_0} - {x_2})}}{y_0} + \frac{{(x - {x_0})(x - {x_2})}}{{({x_1} - {x_0})({x_1} - {x_2})}}{y_1} + \frac{{(x - {x_0})(x - {x_1})}}{{({x_2} - {x_0})({x_2} - {x_1})}}{y_2} P(x)=(x0−x1)(x0−x2)(x−x1)(x−x2)y0+(x1−x0)(x1−x2)(x−x0)(x−x2)y1+(x2−x0)(x2−x1)(x−x0)(x−x1)y2容易看出, P ( x ) P(x) P(x)满足条件 P ( x i ) = y i ( i = 0 , 1 , 2 ) P(x_i)=y_i (i=0,1,2) P(xi)=yi(i=0,1,2)
3. 拉格朗日插值多项式
通过上述描述可以发现,两个插值点可求出一次插值多项式,而三个插值点可求出二次插值多项式。插值点增加到
n
+
1
n+1
n+1 个时,也就是通过
n
+
1
n+1
n+1 个不同的已知点
(
x
i
,
y
i
)
(
i
=
0
,
1
,
⋯
,
n
)
({x_i},{y_i})(i = 0,1, \cdots ,n)
(xi,yi)(i=0,1,⋯,n),来构造一个次数为n的代数多项式
P
(
x
)
P(x)
P(x)。与推导抛物插值的基函数类似,先构造一个特殊
n
n
n 次多项式
l
i
(
x
)
l_i(x)
li(x) 的插值问题,使其在各节点
x
i
x_i
xi 上满足
l
k
(
x
0
)
=
0
,
⋯
,
l
k
(
x
k
−
1
)
=
0
,
l
k
(
x
k
)
=
1
,
l
k
(
x
k
+
1
)
=
0
,
⋯
,
l
k
(
x
n
)
=
0
{l_k}({x_0}) = 0, \cdots ,{l_k}({x_{k - 1}}) = 0,{l_k}({x_k}) = 1,{l_k}({x_{k + 1}}) = 0, \cdots ,{l_k}({x_n}) = 0
lk(x0)=0,⋯,lk(xk−1)=0,lk(xk)=1,lk(xk+1)=0,⋯,lk(xn)=0即
l
k
(
x
i
)
=
δ
k
i
=
{
1
(
i
=
k
)
0
(
i
≠
k
)
l_k(x_i)=\delta _{ki}=\left\{\begin{matrix} 1 & (i=k)\\ 0 & (i\ne k) \end{matrix}\right.
lk(xi)=δki={10(i=k)(i=k)由条件
l
k
(
x
i
)
=
0
,
(
i
≠
k
)
{l_k}({x_i}) = 0,(i \ne k)
lk(xi)=0,(i=k)可知,
x
0
,
x
1
,
⋯
,
x
k
−
1
,
x
k
+
1
,
⋯
,
x
n
{x_0},{x_1}, \cdots ,{x_{k - 1}},{x_{k + 1}}, \cdots ,{x_n}
x0,x1,⋯,xk−1,xk+1,⋯,xn 都是
n
n
n 次
l
k
(
x
)
{l_k}(x)
lk(x) 的零点,故可设
l
k
(
x
)
=
A
k
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
k
−
1
)
(
x
−
x
k
+
1
)
⋯
(
x
−
x
n
)
{l_k}(x) = {A_k}(x - {x_0})(x - {x_1}) \cdots (x - {x_{k - 1}})(x - {x_{k + 1}}) \cdots (x - {x_n})
lk(x)=Ak(x−x0)(x−x1)⋯(x−xk−1)(x−xk+1)⋯(x−xn)其中
A
k
A_k
Ak为待定常数。有条件
l
k
(
x
k
)
=
1
{l_k}({x_k}) = 1
lk(xk)=1,可求得
A
k
{A_k}
Ak为:
A
k
∏
j
=
0
,
j
≠
k
n
(
x
k
−
x
j
)
=
1
{A_k}\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})} = 1
Akj=0,j=k∏n(xk−xj)=1于是
A
k
=
1
∏
j
=
0
,
j
≠
k
n
(
x
k
−
x
j
)
{A_k} = \frac{1}{\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})}}
Ak=∏j=0,j=kn(xk−xj)1代入上式,得
l
k
(
x
)
=
∏
j
=
0
,
j
≠
k
n
(
x
−
x
j
)
∏
j
=
0
,
j
≠
k
n
(
x
k
−
x
j
)
=
∏
j
=
0
,
j
≠
k
n
x
−
x
j
x
k
−
x
j
l_k(x) = \frac{\prod_{j = 0,j \ne k}^n {({x} - {x_j})}}{\prod_{j = 0,j \ne k}^n {({x_k} - {x_j})}} = \prod_{j = 0,j \ne k}^n \frac{{x} - {x_j}}{{x_k} - {x_j}}
lk(x)=∏j=0,j=kn(xk−xj)∏j=0,j=kn(x−xj)=j=0,j=k∏nxk−xjx−xj称
l
k
(
x
)
{l_k}(x)
lk(x)为关于基点
x
i
x_i
xi 的
n
n
n 次插值基函数
(
i
=
0
,
1
,
⋯
,
n
)
(i=0,1,\cdots,n)
(i=0,1,⋯,n),那么以
n
+
1
n+1
n+1个
n
n
n次基本插值多项式
l
k
(
x
)
(
k
=
0
,
1
,
⋯
,
n
)
{l_k}(x)(k = 0,1, \cdots ,n)
lk(x)(k=0,1,⋯,n)为基础,就能直接写出满足插值条件
P
(
x
i
)
=
f
(
x
i
)
(
i
=
0
,
1
,
2
,
⋯
,
n
)
P(x_i)=f(x_i)(i=0,1,2,\cdots,n)
P(xi)=f(xi)(i=0,1,2,⋯,n)的
n
n
n次代数插值多项式
P
(
x
)
=
l
0
(
x
)
y
0
+
l
1
(
x
)
y
1
+
⋯
+
l
n
(
x
)
y
n
P(x) = {l_0}(x){y_0} + {l_1}(x){y_1} + \cdots + {l_n}(x){y_n}
P(x)=l0(x)y0+l1(x)y1+⋯+ln(x)yn其中每个插值基函数
l
k
(
x
)
(
k
=
0
,
1
,
⋯
,
n
)
{l_k}(x)(k = 0,1, \cdots ,n)
lk(x)(k=0,1,⋯,n)都是
n
n
n次值多项式,所以他们的线性组合
P
(
x
)
=
∑
k
=
0
n
l
k
(
x
)
y
k
P(x) = \sum\limits_{k = 0}^n {{l_k}(x){y_k}}
P(x)=k=0∑nlk(x)yk
即为
n
n
n次拉格朗日插值多项式,并记作
L
n
(
x
)
L_n(x)
Ln(x),引入
ω
n
+
1
(
x
)
\omega_{n+1}(x)
ωn+1(x)为
ω
n
+
1
(
x
)
=
(
x
−
x
0
)
(
x
−
x
1
)
⋯
(
x
−
x
n
)
{\omega _{n + 1}}(x) = (x - {x_0})(x - {x_1}) \cdots (x - {x_n}){\rm{ }}
ωn+1(x)=(x−x0)(x−x1)⋯(x−xn)那么得到
ω
′
n
+
1
(
x
k
)
=
(
x
k
−
x
0
)
⋯
(
x
k
−
x
k
−
1
)
(
x
k
−
x
k
+
1
)
⋯
(
x
k
−
x
n
)
{{\omega '}_{n + 1}}({x_k}) = ({x_k} - {x_0}) \cdots ({x_k} - {x_{k - 1}})({x_k} - {x_{k + 1}}) \cdots ({x_k} - {x_n})
ω′n+1(xk)=(xk−x0)⋯(xk−xk−1)(xk−xk+1)⋯(xk−xn) 那么
L
n
(
x
)
L_n(x)
Ln(x)可以转化为
L
n
(
x
)
=
∑
k
=
0
n
y
k
ω
n
+
1
(
x
)
(
x
−
x
k
)
ω
′
n
+
1
(
x
k
)
{L_n}(x) = {\rm{ }}\sum\limits_{k = 0}^n {{y_k}\frac{{{\omega _{n + 1}}(x)}}{{(x - {x_k}){{\omega '}_{n + 1}}({x_k})}}}
Ln(x)=k=0∑nyk(x−xk)ω′n+1(xk)ωn+1(x)
二、Lagrange插值算法及matlab代码
Matlab 版本号 2022b
根据Lagrange 插值算法构建 lagrange.m文件
为了让代码具有可输出性,让大家通俗易懂,编写了一个lab函数,并构建了lab.m文件
1. Lagrange 插值算法matlab实现
下面展示拉格朗日插值函数代码: lagrange.m(复制代码,保存此名称)
function varargout = lagrange(x0,y0,varargin)
% x0 为节点
% y0 为节点对应的函数值
% x 为插值点
m = length(x0);
L1 = zeros(m,m);
l = [];
% step 1 构造基函数lk
for k = 1 : m
V = 1;
for i = 1 : m
if k ~= i
V = conv(V,poly(x0(i))) / (x0(k) - x0(i));
end
end
L1(k,:) = V;
l = cat(1,l,poly2sym(V));
end
fprintf('基函数为:\n');
for k = 1:m
fprintf(['l',lab(k),'(x)=%s\n'],l(k));fprintf('\n');
end
% 通过矩阵乘积求L(x)
L = y0 * l;
L1 = str2sym(['P(x)=',char(L)]);
disp(L1)
% L = simplify(L1);
S = ['$',latex(L1),'$'];
fprintf('拉格朗日多项式为:\nP(x)=%s\n',L);fprintf('\n');
% symdisp(L)
L = matlabFunction(L);
if nargin == 3
varargout{1} = feval(L,varargin{1});
plot(x0,y0,'bo')
hold on
plot(varargin{1},varargout{1},'rp')
plot(min([varargin{1},x0]):0.01:max([varargin{1},x0]),feval(L,min([varargin{1},x0]):0.01:max([varargin{1},x0])),'k-','LineWidth',1)
subtitle(S,'Interpreter','latex','FontSize',14)
title('Lagrange插值','FontSize',14)
legend('原始点','插值点','插值函数P(x)')
else
plot(x0,y0,'bo')
hold on
plot(min(x0):0.01:max(x0),feval(L,min(x0):0.01:max(x0)),'k-','LineWidth',1)
subtitle(S,'Interpreter','latex','FontSize',14)
title('Lagrange插值','FontSize',14)
legend('原始点','插值函数P(x)')
end
end
下面展示lab代码: lab.m(复制代码,保存此名称)
function label = lab(k)
name = {'₀','₁','₂','₃','₄','₅','₆','₇','₈','₉'};
label = '';
k=k-1;
if k == 0
label = name{k+1};
else
while 1
if mod(k,10)==0 && floor(k/10)==0
break
end
j = mod(k,10);
k = floor(k/10);
label = cat(2,name{j+1},label);
end
end
end
2 实例
话不多说,直接讲述lagrange函数使用说明
1.
lagrange(x0,y0): 输入参数只有2个时,x0 为节点,y0 为节点对应的函数值;自动输出:基函数,拉格朗日多项式,插值函数图像
2.y = lagrange(x0,y0,x): 输入参数为3个时,x0 为节点,y0 为节点对应的函数值,x 为插值点;输出:y为插值点对应函数值,自动输出:基函数,拉格朗日多项式,插值函数图像
示例展示一下:
已知
f
(
x
)
f(x)
f(x) 的观测数据为如下表所示,并构造Lagrange插值多项式
| x x x | 0 | 1 | 2 | 4 |
|---|---|---|---|---|
| f ( x ) f(x) f(x) | 1 | 9 | 23 | 3 |
手动计算一下,四个点可构造三次Lagrange插值多项式,其基函数为:
l
0
(
x
)
=
(
x
−
1
)
(
x
−
2
)
(
x
−
4
)
(
0
−
1
)
(
0
−
2
)
(
0
−
4
)
=
−
1
8
x
3
+
7
8
x
2
−
7
4
x
+
1
{l_0}(x) = \frac{{(x - 1)(x - 2)(x - 4)}}{{(0 - 1)(0 - 2)(0 - 4)}} = - \frac{1}{8}{x^3} + \frac{7}{8}{x^2} - \frac{7}{4}x + 1
l0(x)=(0−1)(0−2)(0−4)(x−1)(x−2)(x−4)=−81x3+87x2−47x+1
l
1
(
x
)
=
(
x
−
0
)
(
x
−
2
)
(
x
−
4
)
(
1
−
0
)
(
1
−
2
)
(
1
−
4
)
=
1
3
x
3
−
2
x
2
+
8
3
x
{l_1}(x) = \frac{{(x - 0)(x - 2)(x - 4)}}{{(1 - 0)(1 - 2)(1 - 4)}} = \frac{1}{3}{x^3} - 2{x^2} + \frac{8}{3}x
l1(x)=(1−0)(1−2)(1−4)(x−0)(x−2)(x−4)=31x3−2x2+38x
l
2
(
x
)
=
(
x
−
0
)
(
x
−
1
)
(
x
−
4
)
(
2
−
0
)
(
2
−
1
)
(
2
−
4
)
=
−
1
4
x
3
+
5
4
x
2
−
x
{l_2}(x) = \frac{{(x - 0)(x - 1)(x - 4)}}{{(2 - 0)(2 - 1)(2 - 4)}} = - \frac{1}{4}{x^3} + \frac{5}{4}{x^2} - x
l2(x)=(2−0)(2−1)(2−4)(x−0)(x−1)(x−4)=−41x3+45x2−x
l
3
(
x
)
=
(
x
−
0
)
(
x
−
1
)
(
x
−
2
)
(
4
−
0
)
(
4
−
1
)
(
4
−
2
)
=
1
24
x
3
−
1
8
x
2
+
1
12
x
{l_3}(x) = \frac{{(x - 0)(x - 1)(x - 2)}}{{(4 - 0)(4 - 1)(4 - 2)}} = \frac{1}{{24}}{x^3} - \frac{1}{8}{x^2} + \frac{1}{{12}}x
l3(x)=(4−0)(4−1)(4−2)(x−0)(x−1)(x−2)=241x3−81x2+121x那么Lagrange插值多项式为:
L
3
(
x
)
=
∑
k
=
0
3
y
k
l
k
(
x
)
=
l
0
(
x
)
+
9
l
1
(
x
)
+
23
l
2
(
x
)
+
3
l
3
(
x
)
=
−
11
4
x
3
+
45
4
x
2
−
1
2
x
+
1
\begin{array}{c} {L_3}(x) = \sum\limits_{k = 0}^3 {{y_k}} {l_k}(x) = {l_0}(x) + 9{l_1}(x) + 23{l_2}(x) + 3{l_3}(x) = - \frac{{11}}{4}{x^3} + \frac{{45}}{4}{x^2} - \frac{1}{2}x + 1 \end{array}
L3(x)=k=0∑3yklk(x)=l0(x)+9l1(x)+23l2(x)+3l3(x)=−411x3+445x2−21x+1
接下来利用上述lagrange(x0,y0),检验一下,先构建一个叫demo.m文件,接下来复制此代码放入其中,切记要将demo.m`文件、lagrange.m文件和lab.m文件放在一个文件内(新手注意!!!)
x0 = [0 1 2 4];
y0 = [1 9 23 3];
lagrange(x0,y0);
直接启动运行,输出结果如下,发现和手动计算结果一摸一样
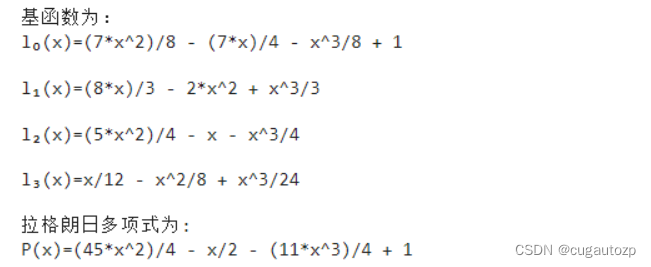
这里代码中还给出了此插值函数的图像
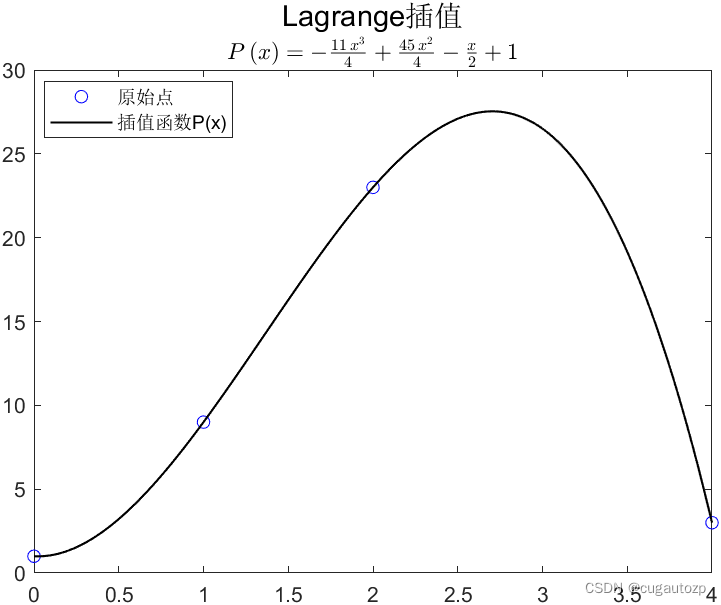
在上述的基础上需要求出当 x = 1.5 , 2.5 , 3 , 3.5 x={1.5, 2.5, 3, 3.5} x=1.5,2.5,3,3.5时,对应的函数值是什么?复制如下代码直接运行看看结果。
x0 = [0 1 2 4];
y0 = [1 9 23 3];
x = [1.5 2.5 3 3.5];
y = lagrange(x0,y0,x)
输出函数值为:

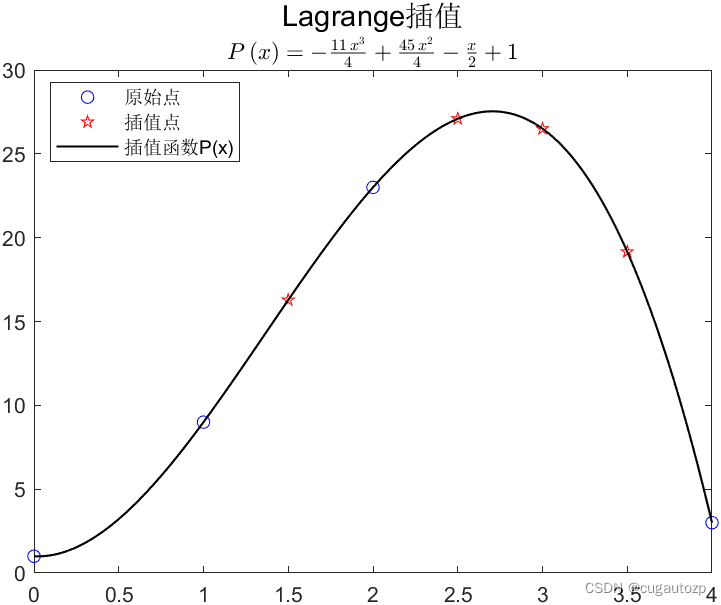
3. 线性插值示意图代码
注意:一定需要有坐标轴工具箱函数否则会报错,请前往上述链接下载。
% 使用了CSDN: Slandarer大佬开源的带箭头的坐标函数包
% 剩余代码由本人撰写
% 此代码为CSDN文章中线性插值示意图代码
% @Author
% Copyright© 2024.3.12
% CSDN name: cugautozp
% GitHub: https://github.com/cug-auto-zp
clc
clear
close all
x=0.2:0.01:1.8;
y=x-exp(x-1);
plot(x,y,'LineWidth',1.5)
% 修改坐标轴属性
ax=gca;
ax.XLim = [0,2];
ax.YLim = [-0.6,0.3];
ax.YTick = [];
ax.XTick = [];
arrowAxes(ax)
x0 = [0.5,1.6];
y0 = x0-exp(x0-1);
hold on
for i=1:length(x0)
plot(x0(i)*[1,1],[-0.6,y0(i)],'LineStyle','--','LineWidth',1.5,'Color',[0,0,0])
text(x0(i)+0.05,(-0.6+y0(i))/2,['$y_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
text(x0(i),-0.65,['$x_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
end
plot(x0,y0,'LineStyle','none','Marker','.','MarkerSize',20,'Color',[1,0,0])
t=polyfit(x0,y0,1);
plot(x,polyval(t,x),'-k','LineWidth',1.5)
text(1,0.1,'$y = f(x)$','Interpreter','latex','FontSize',15,'Color',[0.00,0.45,0.74])
text(0.1,0,'$p(x)=ax+b$','Interpreter','latex','FontSize',15,'Color',[0,0,0])
text(x0(1),y0(1)-0.05,'$A(x_0,f(x_0))$','Interpreter','latex','FontSize',15,'Color',[1,0,0])
text(x0(2),y0(2)-0.05,'$B(x_0,f(x_0))$','Interpreter','latex','FontSize',15,'Color',[1,0,0])
title('线性插值示意图','FontSize',14)
text(-0.1,-0.65,'O','FontSize',15,'Color',[0,0,0])
4. 抛物插值示意图代码
% 使用了CSDN: Slandarer大佬开源的带箭头的坐标函数包
% 剩余代码由本人撰写
% 此代码为CSDN文章中抛物插值示意图代码
% @Author
% Copyright© 2024.3.12
% CSDN name: cugautozp
% GitHub: https://github.com/cug-auto-zp
clc
clear
close all
x=0:0.1:20;
y=-0.5*(x-4).^3+15*(x-4)+6*(x-4).^2+5;
plot(x,y,'LineWidth',1.5)
ax=gca;
ax.XLim = [-1,21];
ax.YLim = [-300,300];
ax.YTick = [];
ax.XTick = [];
arrowAxes(ax)
x0 = [3,9,18];
y0 = -0.5*(x0-4).^3+15*(x0-4)+6*(x0-4).^2+5;
hold on
plot(x0,y0,'LineStyle','none','Marker','.','MarkerSize',20,'Color',[1,0,0])
text(-2,-310,'O','FontSize',15,'Color',[0,0,0])
for i=1:length(x0)
plot(x0(i)*[1,1],[-300,y0(i)],'LineStyle','--','LineWidth',1.5,'Color',[0,0,0])
text(x0(i)+0.3,(-300+y0(i))/2,['$y_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
text(x0(i),-320,['$x_',num2str(i-1),'$'],'Interpreter','latex','FontSize',15,'Color',[0,0,0])
end
t=polyfit(x0,y0,2);
plot(x,polyval(t,x),'-k','LineWidth',1.5)
text(15,200,'$y = f(x)$','Interpreter','latex','FontSize',15,'Color',[0.00,0.45,0.74])
text(3,150,'$y = L_2(x)$','Interpreter','latex','FontSize',15,'Color',[0,0,0])
title('抛物插值示意图')
三、总结
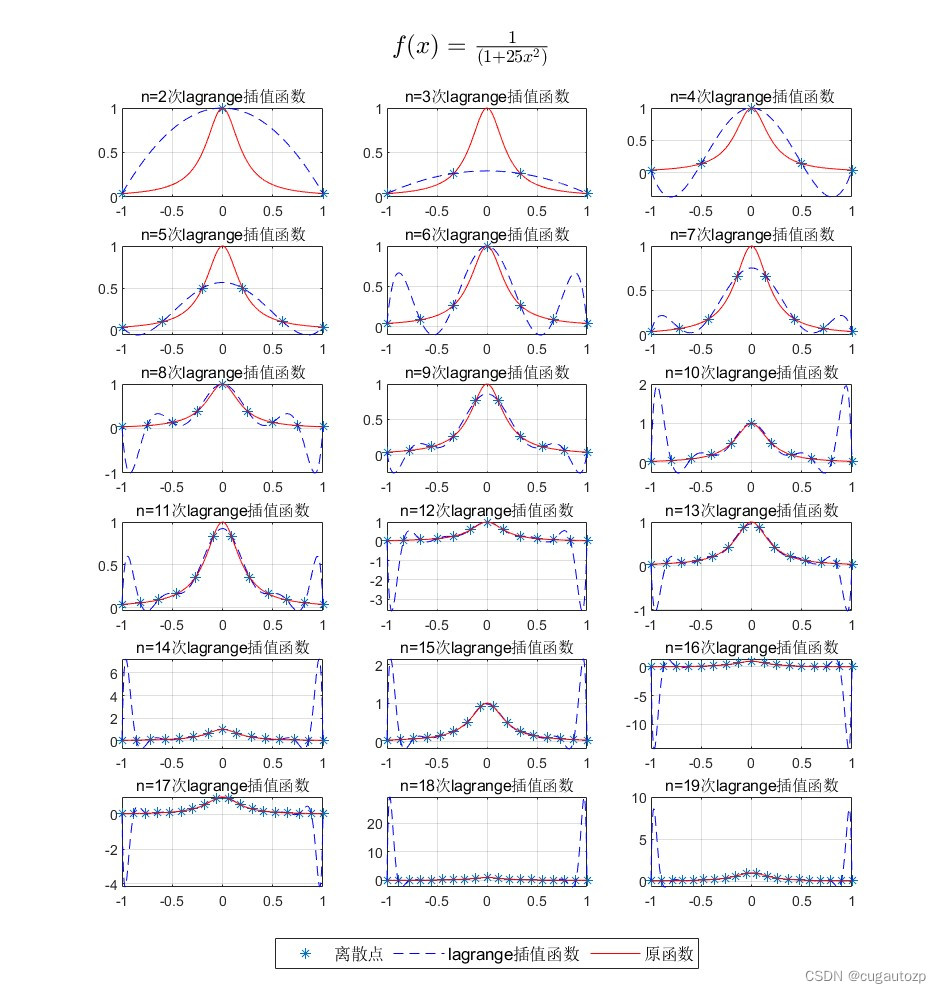
此次内容主要讲的是拉格朗日插值的原理,及根据原理利用matlab编写一个通用计算公式函数,然后举例来验证代码的正确性。为了方便,这里直接将函数图像,以及中间过程的基函数和最后的插值函数都自动输出,非常方便。如果对拉格朗日插值有兴趣的话可以更加深入的做一做一下实验,还蛮有意思的。
四、插值法专栏
专栏链接:插值法专栏,如果对你有帮助的话可以点个赞,点个订阅,我将完善此专栏
- 数值分析(一) 牛顿插值法及matlab代码
- 数值分析(二) 三次样条插值法matlab程序
- 数值分析(二续) 三次样条插值二类边界完整matlab代码
- 数值分析(三) Lagrange(拉格朗日)插值法及Matlab代码实现
- 数值分析(四) Hermite(埃尔米特)插值法及matlab代码