目录

引言

一、线性数据结构

1. 1 数组（Array）

1.2 链表（Linked List）

1.3 栈（Stack）

1.4 队列（Queue）

二、图形数据结构

2.1 深度优先搜索（DFS）：

2.2 广度优先搜索（BFS）：

2.3 Dijkstra算法：

2.4 Floyd-Warshall算法：

2.5 Prim算法和Kruskal算法：

2.6 拓扑排序：

2.7 强连通分量：

2.8 贝尔曼-福特算法（Bellman-Ford）：

三、树形数据结构

3.1 树的遍历算法：

3.2 二叉树相关算法：

3.3 构建算法：

3.4 平衡二叉树算法：

1 AVL树

2 红黑树

3 B树和B+树算法：

4 并查集（Disjoint Set）算法：

5 表达式树算法：

四、经典算法

4.1 常见的经典算法

4.1.1线性算法

4.1.2 对数算法

4.1.3 平方算法

4.1.4 指数算法

4.2 分类

4.2.1 排序算法

4.1.2 动态规划算法

4.3 机器学习和数据挖掘领域

4.3.1贝叶斯算法

4.3.2 决策树

4.3.3 KNN算法

4.3.4 神经网络

4.4 特定问题算法

4.4.1 Dijkstra算法

4.4.2 单纯型算法

4.4.3 分支界定算法

总结

---

 

引言

算法与数据结构是计算机科学中的两个核心概念，它们共同构成了计算机程序设计和实现的基础。简单来说，数据结构是组织和管理数据的方式，而算法则是解决问题的方法和步骤。

数据结构主要关注数据元素之间的关系以及数据的存储和访问方式。通过合理地组织数据，数据结构可以大大提高程序的效率和性能。常见的数据结构包括数组、链表、栈、队列、树和图等，每种数据结构都有其特定的应用场景和优势。

而算法则是解决特定问题的步骤和方法的描述。一个好的算法应该具备高效性、正确性和可读性等特点。算法的设计和实现需要考虑到问题的性质、数据的规模以及计算机的性能等因素。常见的算法包括排序算法、查找算法、图算法等，这些算法在各个领域都有着广泛的应用。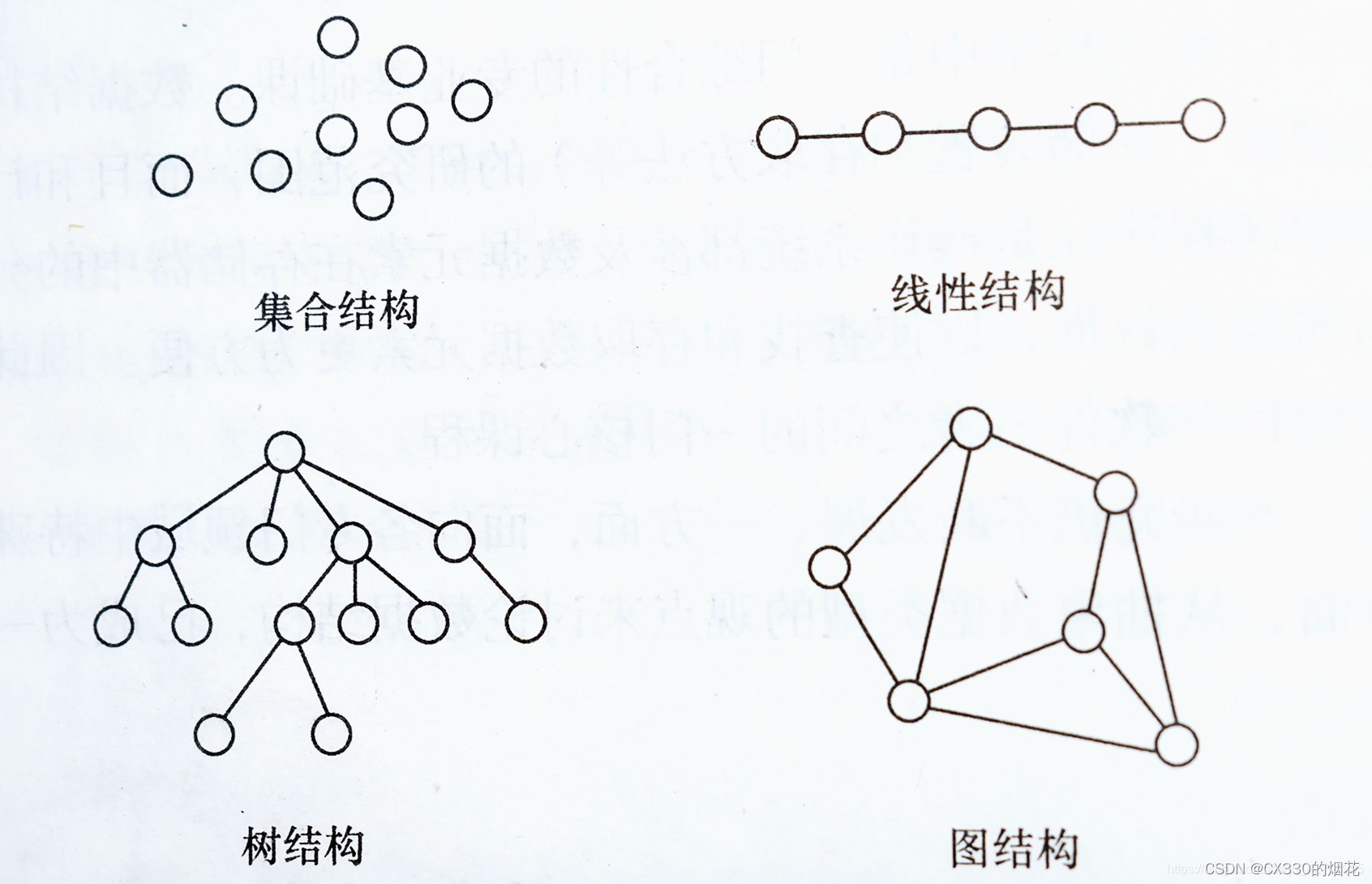

一、线性数据结构

1. 1 数组（Array）

数组是一种线性数据结构，用于存储相同类型的元素。数组中的每个元素都可以通过索引直接访问，这使得数组在随机访问元素时非常高效。然而，数组的大小在创建时是固定的，如果需要添加或删除元素，可能需要重新分配内存并复制数据，这可能会导致性能开销。

1.2 链表（Linked List）

链表也是线性数据结构的一种，由一系列节点组成。每个节点包含数据和指向下一个节点的指针。链表可以动态地添加和删除元素，只需要修改相应节点的指针即可。链表克服了数组大小固定的缺点，但访问特定元素需要从头节点开始遍历，因此随机访问的效率较低。

1.3 栈（Stack）

栈是一种后进先出（LIFO）的线性数据结构。它只允许在一端（称为栈顶）进行插入和删除操作。栈在函数调用、撤销操作、括号匹配等场景中有着广泛的应用。

1.4 队列（Queue）

队列是一种先进先出（FIFO）的线性数据结构。它允许在一端（称为队尾）插入元素，在另一端（称为队头）删除元素。队列在缓冲区管理、任务调度等场景中非常有用。

二、图形数据结构

 

图形数据结构相关的算法多种多样，每种算法都针对图形数据结构的特定问题提供了解决方案。以下是一些常见的图形数据结构算法：

2.1 深度优先搜索（DFS）：

1. 用于遍历或搜索树或图的算法。这个算法会尽可能深地搜索图的分支。
2. 应用：用于检测图中的环、拓扑排序、求解迷宫问题等。

2.2 广度优先搜索（BFS）：

1. 从图的某一顶点出发，访问所有相邻的顶点，然后再访问这些顶点的相邻顶点，如此类推。
2. 应用：用于求解最短路径问题（在无权图中）、查找最小生成树（在某些算法中）。

2.3 Dijkstra算法：

1. 用于带权有向图中单源最短路径问题的求解。
2. 应用：在路由选择、物流规划等领域有广泛应用。

2.4 Floyd-Warshall算法：

1. 用于求解所有顶点对之间的最短路径问题。
2. 应用：在需要计算图中任意两点间最短路径的场景下非常有用，如社交网络中的距离计算。

2.5 Prim算法和Kruskal算法：

1. 用于构建图的最小生成树。最小生成树是连接图中所有顶点的边权和最小的树。
2. 应用：在通信网络、电路设计等领域，用于寻找成本最低的连接方案。

2.6 拓扑排序：

1. 对有向无环图（DAG）的顶点进行线性排序，使得对每一条有向边(u, v)，均有u（在排序记录中）比v先出现。
2. 应用：常用于任务调度、课程安排等场景。

2.7 强连通分量：

1. 在有向图中，如果任意两个顶点都存在从一方到另一方的路径，则称该有向图是强连通的。强连通分量是图的最大强连通子图。
2. 应用：在社交网络分析、程序依赖关系分析等中有重要作用。

2.8 贝尔曼-福特算法（Bellman-Ford）：

1. 用于在带权有向图中计算单源最短路径。与Dijkstra算法不同，它可以处理带有负权边的图。
2. 应用：在网络路由、交通规划等领域。

这些算法为图形数据结构提供了强大的支持，使我们能够解决各种问题，从简单的遍历到复杂的优化问题。不同的算法针对特定的问题和场景，选择合适的算法对于问题的有效解决至关重要。

三、树形数据结构

树形数据结构相关的算法丰富多样，每种算法都针对树形数据结构的特定问题提供了解决方案。以下是一些常见的树形数据结构算法：

3.1 树的遍历算法：

1. 前序遍历：先访问根节点，然后遍历左子树，最后遍历右子树。
2. 中序遍历：先遍历左子树，然后访问根节点，最后遍历右子树。在二叉搜索树中，中序遍历的结果是有序的。
3. 后序遍历：先遍历左子树，然后遍历右子树，最后访问根节点。
4. 层次遍历：按树的层次，从上到下、从左到右遍历节点。这通常通过队列实现。

3.2 二叉树相关算法：

1. 查找特定值的节点：通过遍历树来查找具有特定值的节点。
2. 插入节点：在二叉搜索树中插入新节点，同时保持树的搜索属性。
3. 删除节点：从二叉搜索树中删除指定节点，同时保持树的搜索属性。

3.3 构建算法：

1. 构建哈夫曼树：用于数据压缩的算法，根据字符出现的频率构建最优二叉树。
2. 构建堆：将无序数组构造成最大堆或最小堆，以便进行堆排序或实现优先队列。

3.4 平衡二叉树算法：

1 AVL树

通过旋转操作来保持树的平衡，确保树的高度为O(log n)。

2 红黑树

一种自平衡的二叉搜索树，通过颜色和一系列调整操作来保持树的平衡。

3 B树和B+树算法：

用于数据库和文件系统的索引结构，能够保持数据有序，同时支持高效的插入、删除和查找操作。

4 并查集（Disjoint Set）算法：

用于处理一些不相交集合（Disjoint Sets）的合并及查询问题。常常使用树（森林）来表示集合。

5 表达式树算法：

用于表示和计算数学表达式，树中的每个节点代表一个运算符或操作数。

这些算法为处理树形数据结构提供了强大的支持，从基本的遍历操作到复杂的构建和优化算法，都为我们解决实际问题提供了有效的手段。根据具体的应用场景和需求，选择合适的算法对于问题的有效解决至关重要。

四、经典算法

4.1 常见的经典算法

4.1.1线性算法

这类算法的时间复杂度为O(n)，执行时间随问题规模线性增长。例如，遍历一个数组就是一个线性算法的例子。

4.1.2 对数算法

这类算法的时间复杂度为O(log n)，执行时间随问题规模呈对数增长。二分查找就是一个典型的对数算法。

4.1.3 平方算法

这类算法的时间复杂度为O(n^2)，执行时间随问题规模呈平方增长。冒泡排序是一个平方算法的例子。

4.1.4 指数算法

这类算法的时间复杂度为O(2^n)，执行时间随问题规模呈指数增长。求解旅行商问题就是一种指数算法。

4.2 分类

4.2.1 排序算法

用于将一组数据按照一定的顺序排列。常见的排序算法包括冒泡排序、快速排序、插入排序、选择排序和归并排序等。

4.1.2 动态规划算法

通过将一个问题分解为子问题来求解原问题。子问题的解被存储和重用以减少计算量。

4.3 机器学习和数据挖掘领域

4.3.1贝叶斯算法

用于概率建模和推理，常被用于垃圾邮件过滤、情感分析、股票市场预测、文档分类等。

4.3.2 决策树

常用于分类和回归问题，比如客户分群、贷款审批、营销策略等。

4.3.3 KNN算法

可以用于聚类分析、预测分析、搜索引擎、文本分类等场景。

4.3.4 神经网络

可以用于图像识别、语音识别、自然语言理解等，以及股票市场预测、智能推荐、自动驾驶等。

4.4 特定问题算法

4.4.1 Dijkstra算法

针对没有负值权重边的有向图，计算其中的单一起点最短路径。

4.4.2 单纯型算法

在数学的优化理论中，用于找到线性规划问题的数值解。

4.4.3 分支界定算法

在多种最优化问题中寻找特定最优化解决方案的算法，特别是针对离散、组合的最优化问题。

这些经典算法在计算机科学、数学、统计学等多个领域中都发挥着重要的作用，为解决各种复杂问题提供了有效的工具和方法。

总结

算法和数据结构是相辅相成的。数据结构为算法提供了基础，而算法则利用数据结构来解决实际问题。在学习算法和数据结构时，我们需要掌握它们的基本概念、原理和应用方法，以便能够灵活地运用它们来解决实际问题。

在现代社会中，算法和数据结构的应用已经渗透到各个领域。无论是互联网、人工智能、大数据还是其他领域，都需要借助算法和数据结构来解决复杂的问题。因此，掌握算法和数据结构的知识对于计算机专业人士来说至关重要。

综上所述，算法与数据结构是计算机科学中不可或缺的两个概念。它们不仅是我们理解计算机程序运行原理的关键，更是我们解决实际问题的重要工具。通过学习算法和数据结构，我们可以提高程序的效率和性能，为解决各种复杂问题提供有力的支持。