目录
选择题
编程题
寻找奇数
寻找峰值
选择题
1、有如下代码,则*(p[0]+1)所代表的数组元素是
int a[3][2] = {1, 2, 3, 4, 5, 6}, *p[3];
p[0] = a[1];- A
a[0][1] - B
a[1][0] - C
a[1][1] - D
a[1][2]
答案:C
解析:
本题定义了一个3行2列的二维数组,那么一行最多只能有两个元素,所以按数组元素顺序排列如下图所示
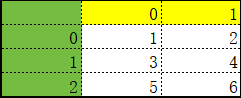
因为数组p为元素类型是指针类型数组,并且第一个元素为二维数组第二行的第一个元素的地址,即a[1][0]的地址,所以*(p[0]+1)为第二行第二列的的元素,
即p[0][1] == a[1][1]
2、(多选题)关于指针下列说法正确的是
- A 任何指针都可以转化为
void * - B
void *可以转化为任何指针 - C 指针的大小为8个字节
- D 指针虽然高效、灵活但可能不安全
答案:ABD
解析:
C选项,指针占几个字节要看平台,64位环境下8个字节,32位环境下4个字节,其余选项正确
3、以下scanf函数调用选项中, 错误的是
struct T
{
char name[20];
int age;
int sex;
} a[5], *pa=a;- A
scanf("%s",a[0].name); - B
scanf("%d", &pa[0].age); - C
scanf("%d",&(pa->age)); - D
scanf("%d", pa->age);
答案:D
解析:
该题考察的是通过scanf函数的调用对结构体数据类型进行初始化。scanf("输入控制符", 输入参数);功能:将从键盘输入的字符转化为“输入控制符”所规定格式的数据,然后存入以输入参数的值为地址的变量中。scanf输入时要通过地址找空间,B、C用了&是正确的。name属于字符数组的数组名,相当于数组的首地址,A正确。单独的pa->age可用于输出语句获取值的形式,用在scanf中的时候需要&操作符,D错误
4、如下函数fun计算prod=1*2*3*…*n,并返回计算结果值。但当n>12时,返回值不正确。要找出该程序的错误,正确的调试方法是
int fun(int n)
{
int prod = 1 , i = 0;
for(i = 1;i <= n;i++)
{
prod *= i;
}
return prod;
}- A 监视变量
prod的值,在prod *= i;行处设置断点,然后单步运行,直到发现错误原因 - B 监视变量
prod的值,在return prod;行处设置断点,程序中断后,即可发现错误原因 - C 在
prod=1;处设置断点,然后在函数调用堆栈中即可发现错误原因 - D 监视变量
i的值,在for (i=1; i<=n; i++)行处设置断点,然后单步运行,直到发现错误原因
答案:A
解析:
依题目已知情况,当n<=12时结果是正确的,说明是随着参数的变大计算过程中哪里出了问题,故而要在prod *= i;处设断点,查看原因。错误原因是数据过大时整型溢出
5、下列给定程序中,函数fun的功能是:把形参a所指数组中的奇数按原顺序依次存放到a[0]、a[1]、a[2]…中,把偶数从数组中删除,奇数个数通过函数值返回。 例如,若a所指数组中的数据最初排列为:9,1,4,2,3,6,5,8,7,删除偶数后,a所指数组中的数据为:9,1,3,5,7,返回值为5。请在程序的下画线处填入正确的内容并将下画线删除,使程序得出正确的结果
int fun(int a[], int n)
{
int i, j;
j=0;
for (i=0; i<n; i++)
if (a[i]%2== _________ )
{
a[j]=a[i];
_________;
}
return _________;
}- A
0 j++ j - B
1 j++ j+1 - C
0 j++ j+1 - D
1 j++ j
答案:D
解析:
代码实现的思路应该是arr[i]是奇数的时候要存储起来,所以第一个空是1,最开始j是0,每次找到一个奇数就存储到arr[j]的位置,那接下里j需要+1,所以得第二个空是j++,当循环停止的时候,j其实就是奇数的个数。所以最后返回j,第三个空是j。所以选D。
编程题
寻找奇数
题目链接:寻找奇数_牛客题霸_牛客网 (nowcoder.com)
描述
现在有一个长度为 n 的正整数序列,其中只有一种数值出现了奇数次,其他数值均出现偶数次,请你找出那个出现奇数次的数值。
数据范围: 1≤ n≤
输入描述:
第一行:一个整数n,表示序列的长度。第二行:n个正整数ai,两个数中间以空格隔开。
输出描述:
一个数,即在序列中唯一出现奇数次的数值。
思路解析:
本题注意到题目说出现奇数次的数值只有一个,其余数值均出现偶数次,可以考虑对数组整体进行异或
参考代码:
#include <stdio.h>
#include <stdlib.h>
int main() {
int num = 0;
int ret = 0;
scanf("%d",&num);
int* data = (int*)malloc(sizeof(int)*num);
for (int i = 0; i < num; i++) {
scanf("%d", &data[i]);
ret ^= data[i];
}
printf("%d",ret);
return 0;
}寻找峰值
题目链接:寻找峰值_牛客题霸_牛客网 (nowcoder.com)
描述
给定一个长度为n的数组nums,请你找到峰值并返回其索引。数组可能包含多个峰值,在这种情况下,返回任何一个所在位置即可。
1.峰值元素是指其值严格大于左右相邻值的元素。严格大于即不能有等于
2.假设nums[-1] = nums[n] = −∞
3.对于所有有效的i都有nums[i] != nums[i + 1]
4.你可以使用O(logN)的时间复杂度实现此问题吗?
数据范围:
1≤ nums. length≤
<= nums[ i]<=
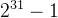
思路解析:
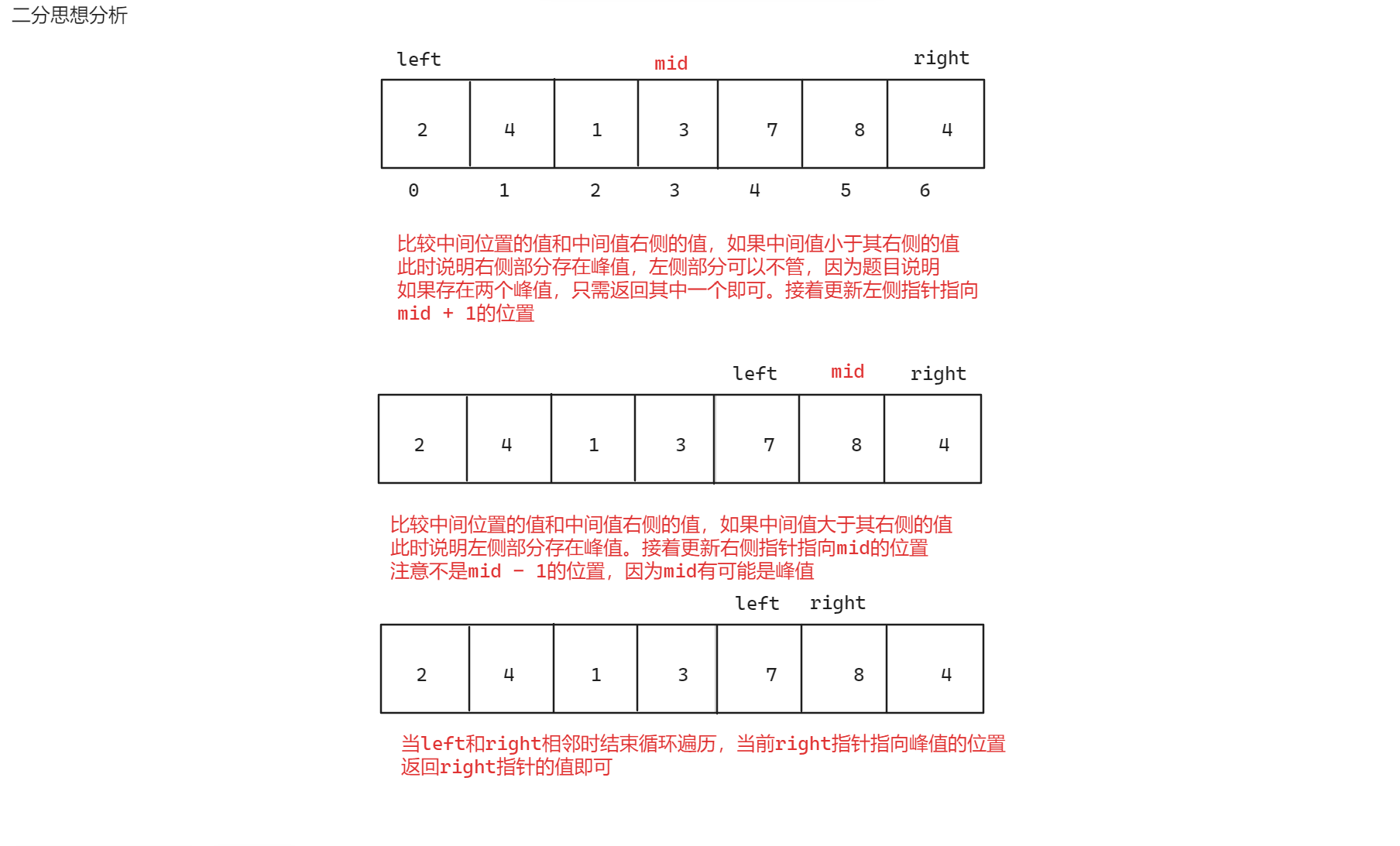
本题可以采用暴力求解找到峰值,但是题目规定使用O(logN)的时间复杂度,而暴力求解的时间复杂度为O(N),所以考虑采用二分查找的思想或者递归
首先考虑递归思想,在递归思想中,使用两个指针left和right分别控制左区间和右区间,以每一个区间的中间位置为界限将数组数值分为两部分,当left和right指针同时指向同一个位置时递归结束返回当前下标,当递归结束返回后比较两个下标对应数值的大小,返回较大值的下标,具体过程如下:(当前区间为[left, mid][mid + 1, right])
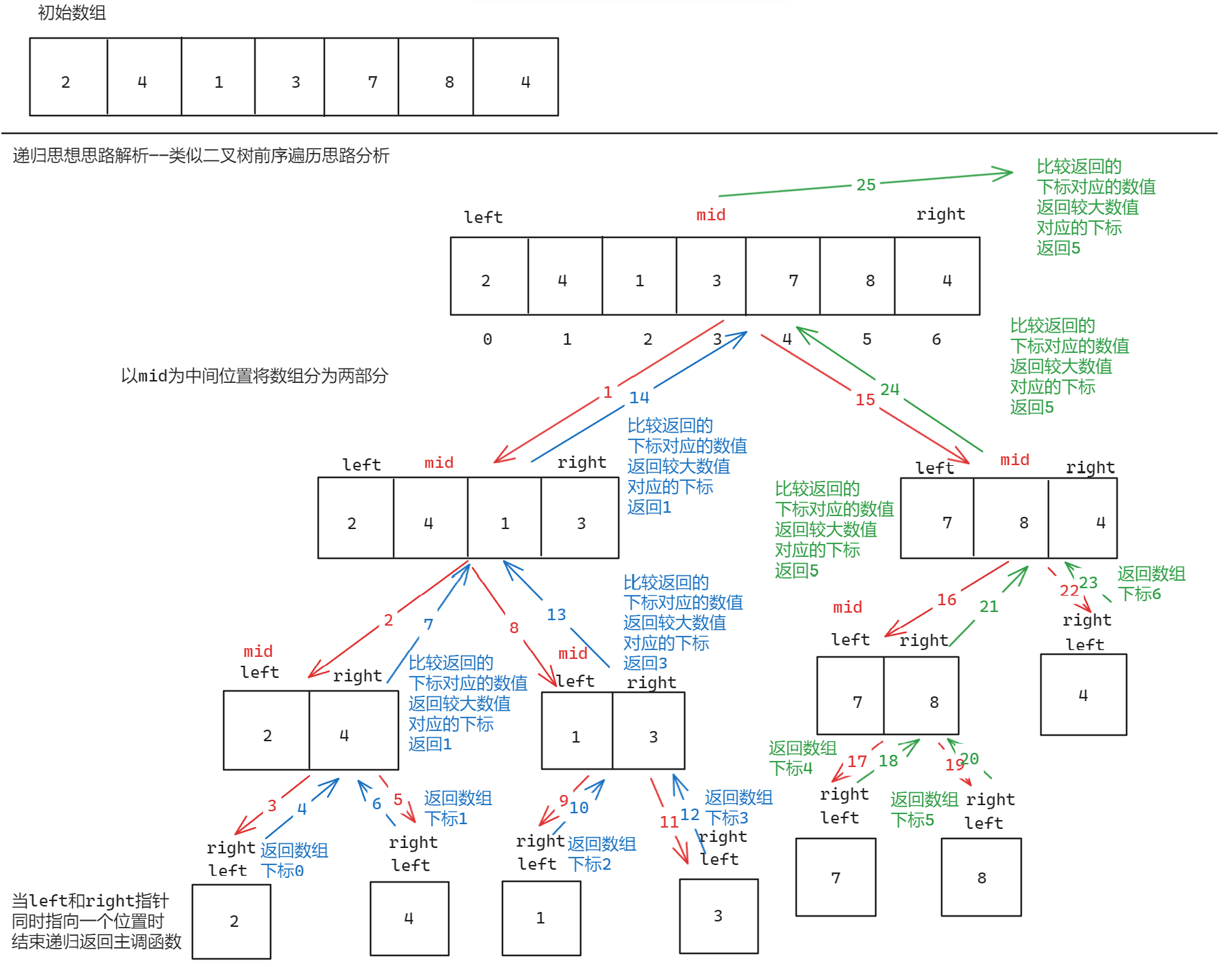
需要注意的是,分割后的区间不可以是[left, mid - 1][mid, right],因为会出现无穷递归,具体原因如下:

第二个是二分查找的思想,具体思路如下:
需要注意的是,使用二分查找思想需要判断当峰值出现在第一个元素和最后一个元素的位置
参考代码
二分查找思想
int findPeakElement(int* nums, int numsLen) {
if(numsLen == 1 || nums[0] > nums[1])
{
return 0;
}
if(nums[numsLen - 1] > nums[numsLen - 2])
{
return numsLen - 1;
}
int left = 0;
int right = numsLen - 1;
while (left < right) {
int mid = (left + right) / 2;
if(nums[mid] > nums[mid + 1])
{
right = mid;
}
else {
left = mid + 1;
}
}
return right;
}递归思想
int _findPeakElement(int* nums, int left, int right) {
if (left >= right) {
return left;
}
int mid = (left + right) / 2;
int leftSummit = _findPeakElement(nums, left, mid);
int rightSummit = _findPeakElement(nums, mid + 1, right);
return nums[leftSummit] > nums[rightSummit] ? leftSummit : rightSummit;
}
int findPeakElement(int* nums, int numsLen) {
int ret = _findPeakElement(nums, 0, numsLen - 1);
return ret;
}