本笔记简单记录链式法则的原理，关于链式法则，本身和高等数学中的链式求导法则是一样的，深度学习中相关资料可以参考这里：

【深度学习之美22】BP算法详解之链式法则 - 知乎10.5 什么是计算图？我们知道， 神经网络的学习本质，就是找到网络中神经元之间的最佳连接权值。如何快速找到这个最佳权值，是有学问的。通常我们利用数值微分来计算神经网络权值参数的梯度，用梯度下降等策略来确…https://zhuanlan.zhihu.com/p/44138371        

import tensorflow as tf
import numpy as np

tf.__version__

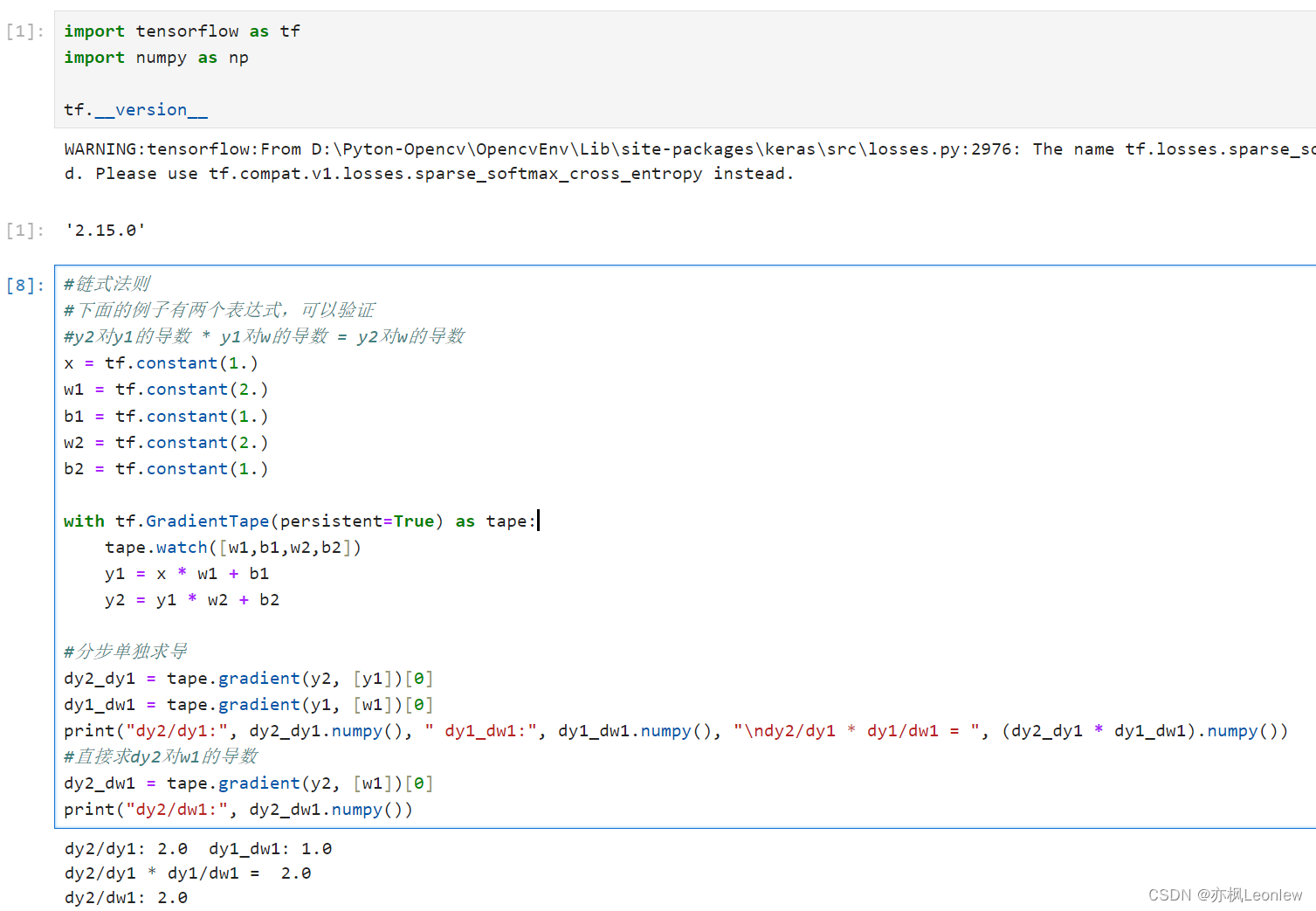
#链式法则
#下面的例子有两个表达式，可以验证
#y2对y1的导数 * y1对w的导数 = y2对w的导数
x = tf.constant(1.)
w1 = tf.constant(2.)
b1 = tf.constant(1.)
w2 = tf.constant(2.)
b2 = tf.constant(1.)

with tf.GradientTape(persistent=True) as tape:
    tape.watch([w1,b1,w2,b2])
    y1 = x * w1 + b1
    y2 = y1 * w2 + b2

#分步单独求导
dy2_dy1 = tape.gradient(y2, [y1])[0]
dy1_dw1 = tape.gradient(y1, [w1])[0]
print("dy2/dy1:", dy2_dy1.numpy(), " dy1_dw1:", dy1_dw1.numpy(), "\ndy2/dy1 * dy1/dw1 = ", (dy2_dy1 * dy1_dw1).numpy())
#直接求dy2对w1的导数
dy2_dw1 = tape.gradient(y2, [w1])[0]
print("dy2/dw1:", dy2_dw1.numpy())

运行结果如下：