在学习并查集的应用之前,请大家先学习第六期-并查集的入门 ,这样会比较好理解
真题训练1
合根植物2017年第八届决赛,lanqiao0J题号110
【题目描述】
w 星球的一个种植园,被分成 m×n 个小格子(东西方向 m 行,南北方向 n 列)。每个格子里种了一株合根植物。这种植物有个特点,它的根可能会沿着南北或东西方向伸展,从而与另一个格子的植物合成为一体。如果我们告诉你哪些小格子间出现了连根现象,你能说出这个园中一共有多少株合根植物吗?
【输入描述】
第一行,两个整数 m,n,用空格分开,表示格子的行数、列数(1≤m,n≤1000)。
接下来一行,一个整数 k (0≤k≤10^5 ),表示下面还有 k 行数据。
接下来 k 行,每行两个整数 a,b,表示编号为 a 的小格子和编号为 b 的小格子合根了。
格子的编号一行一行,从上到下,从左到右编号。
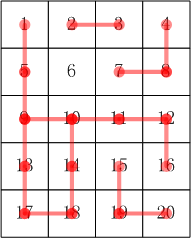
比如:5×4 的小格子,编号:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20【输出描述】
输出植物数量。
【输入输出样式】
输入
5 4 16 2 3 1 5 5 9 4 8 7 8 9 10 10 11 11 12 10 14 12 16 14 18 17 18 15 19 19 20 9 13 13 17输出
5样例说明
其合根情况参考下图:
【解题思路】
- 用并查集处理所有的合并
- 法一:处理完后,检查所有S[i]= i的数量,也就是集等于自己的数量,就是答案
- 法二:总共有m*n棵植物,记为ans。每合并一次ans就减一。完成k次合根后的ans就是答案。
【代码】
法一:
def init_set(n): #初始化
for i in range (n):
s. append(i)
def find_set(x): #有路径压缩优化的查询
if x != s[x]: # 不等于自己的集
s[x] = find_set(s[x]) # 把集改成根节点的集
return s[x]
def merge_set(x,y): #合并
x = find_set(x)
y = find_set(y)
if x != y: s[x] = s[y]
n,m = map(int,input().split())
k = int(input())
# s = [i for i in range(0,n*m+1)] # 替代初始化函数
s = []
init_set(n*m+1)
for i in range(k):
x,y = map(int,input().split())
merge_set(x,y)
# print(s)
ans = 0
for i in range(1,n*m+1):
if i == s[i]:
ans +=1
print(ans)法二:
def find_set(x): #有路径压缩优化的查询
if x != s[x]: # 不等于自己的集
s[x] = find_set(s[x]) # 把集改成根节点的集
return s[x]
def merge_set(x,y): #合并
x = find_set(x)
y = find_set(y)
if x == y: return False
s[x] = s[y]
return True
m,n =map(int,input ().split())
k = int (input())
s = list(range (m*n))
ans = m*n
for i in range(k):
x,y = map (int,input (). split() )
if merge_set(x,y):
ans -= 1
print(ans)真题训练2
修改数组2019年第十届省赛,lanqiaoOJ题号185
题目描述
给定一个长度为 N 的数组 A=[A1,A2,⋅⋅⋅,AN],数组中有可能有重复出现的整数。现在小明要按以下方法将其修改为没有重复整数的数组。小明会依次修改A2,A3,⋅⋅⋅,AN。
当修改 Ai 时,小明会检查Ai 是否在 中出现过。如果出现过,则小明会给 Ai 加上 1 ;如果新的 Ai 仍在之前出现过,小明会持续给 Ai 加 1 ,直 到 Ai 没有在中出现过。
当 AN 也经过上述修改之后,显然 A 数组中就没有重复的整数了。
现在给定初始的 A 数组,请你计算出最终的 A 数组。
输入描述
第一行包含一个整数 N(1≤N≤100000)第二行包含 N 个整数 A1,A2,⋅⋅⋅,AN*(1≤Ai≤1000000)
输出描述
输出 N 个整数,依次是最终的 A1,A2,⋅⋅⋅,AN。输入输出样例
输入5
2 1 1 3 4
输出2 1 3 4 5
【题目提取】
功能:把数组的数字转换为都不重复·数组A=[A1,A2,... ,AN]
- 依次修改A2,A3,... ,AN
- 修改Ai时,检查A;是否在
中出现过。如果出现过,给Ai加上1;
- 如果新的Ai仍在之前出现过,持续给A;加1,直到Ai没有在
中出现过。
【问题解析】
法一:暴力法
数据规模:1≤N≤100000
每读入一个新的数,就检查前面是否出现过,每一次需要检查前面所有的数。共有n个数,每个数检查O(n)次,总复杂度O(n^3),超时。
下面有两种写法:
n = int(input ())
a = [int(i) for i in input(). split()]
for i in range(1, n) : #从第2个开始: a[1]
for k in range(i) :# 有些数与前面不止做一次检查;有的需要加1后再检查,与同一个数做k次检查
for j in range(i): # 与前面的数做检查
if a[i] == a[j]:
a[i]+=1
for i in range(n): print(a[i], end=' ')
#for i in a: print(i, end=' ')第二种写法比较好理解
n = int(input())
a = [int(i) for i in input ().split()]
for i in range(1, n): #从第2个开始: a[1]
for j in range(i): #检查它前面的所有数
while a[i] in a[0:i]: # 前面存在过就加一
a[i]+=1
for i in a:
print(i, end=' ')可以通过30%的测试。
法二:查重,hash或set ()
- 改进,用hash。定义vis[ ]数组,vis[i]表示数字i是否已经出现过。这样就不用检查前面所有的数了,基本上可以在O(1)的时间内定位到。
- 或:直接用set判断是否重复,也是O(1)。
复杂度:O(n^2)
n = int (input())
a = [int (i) for i in input ().split()]
s = set()
for i in range (n):
while a[i] in s:
a[i] += 1
s.add(a[i])
for i in a: print (i, end=' ')可以通过60%的测试。
法三:并查集求解
本题特殊要求:“如果新的Ai仍在之前出现过,小明会持续给Ai加1,直到A,没有在中出现过。”这导致在某些情况下,仍然需要大量的检查。
以5个6为例:A={6,6,6,6,6}。
- 第一次读A[1]=6,设置vis[6]=1。
- 第二次读A[2]=6,先查到vis[6]=1,则把A[2]加1,变为A[2]=7;再查vis[7]=0,设置vis[7]=1。检查了2次。
- 第三次读A[3]=6,先查到vis[6]=1,则把A[3]加1得A[3]=7﹔再查到vis[7]=1,再把A[3]加1得A[3]=8,设置vis[8]=1;最后查vis[8]=0,设置vis[8]=1。检查了3次。
每次读一个数,仍需检查O(n)次,总复杂度O(n^2)。
本题用Hash,在特殊情况下仍然需要大量的检查。
问题出在“持续给A;加1,直到Ai没有在中出现过”。
也就是说,问题出在那些相同的数字上。当处理一个新的Ai时,需要检查所有与它相同的数字。
如果把这些相同的数字看成一个集合,就能用并查集处理。
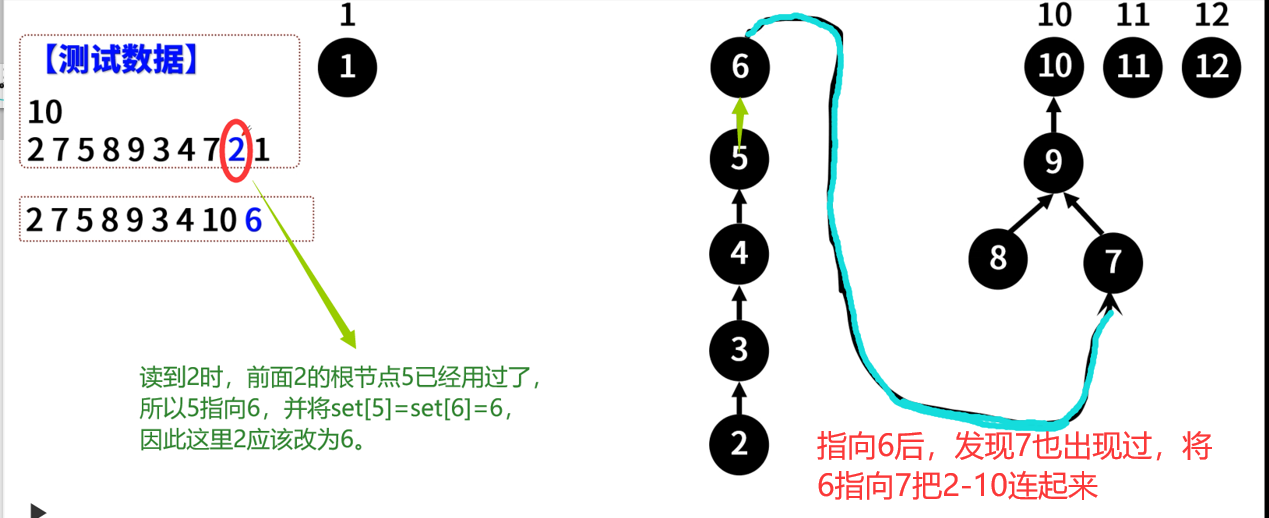
这个算法的优化方向:对每个A,如果出现过,必须快速找到比Ai大的、连续的数的最大值,例如,如果前面的整数依次为2,7,5,8,9,3,4,再读入一个整数7,则前面的7、8、9是连续的,应该把新出现的7改成10。——用并查集来实现。
首先设置一个set数组,这个数组所有的元素都指向自身(初始化),s[i]表示当你访问到 i 个数时应该把他换成什么。
(1)、一开始都是s[ i ] 指向i ,也就说明都没访问过
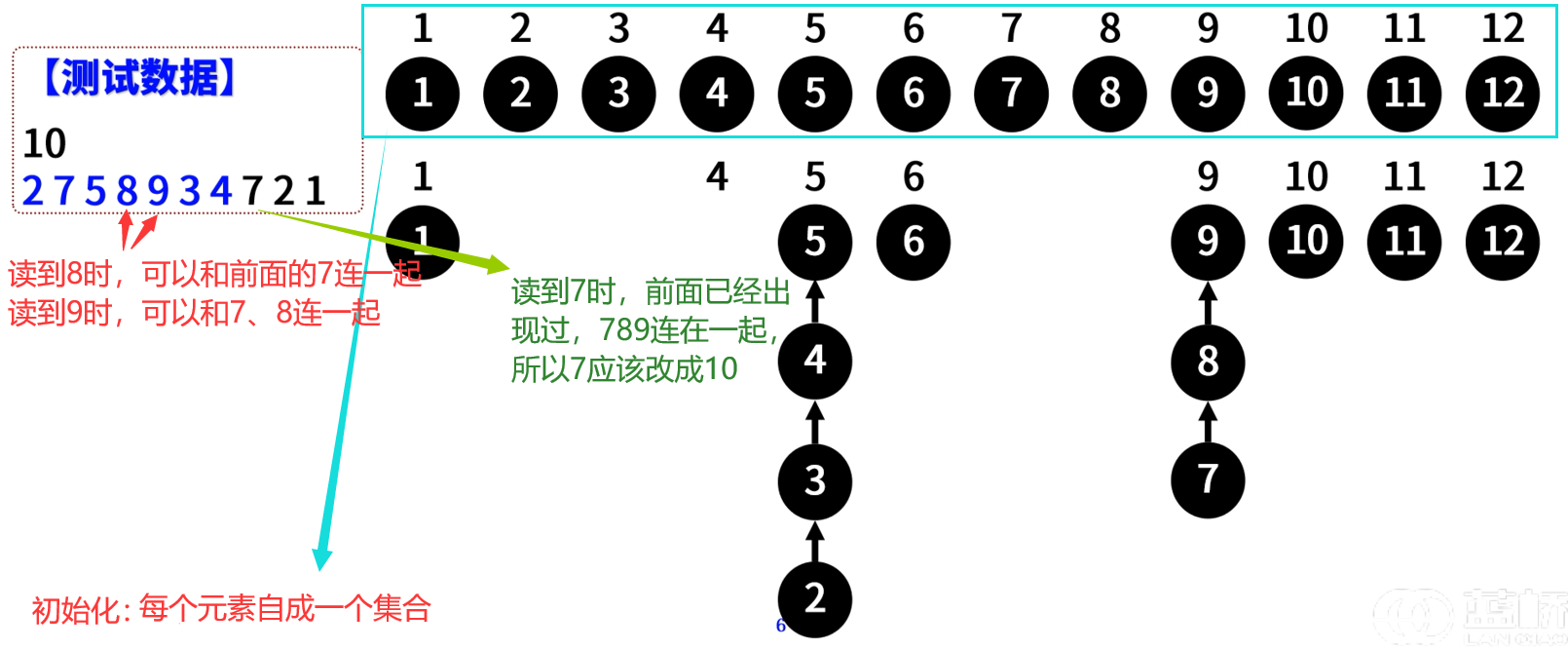
(2)、当你访问了 i 以后,就需要进行更新,更新s[i] = s[i+1](下图中为指向下一个结点)。因为有时候有些数据是重复的(例如下图中7这个数据),所以当我们再次访问到i(下图中的7)的时候,i已经输出过了,这时候我们需要输出的i+1,但是i+1也有可能输出过了,所以说我们就输出的是s[i+1] (递归:s[i+1]=s[8]=s[9]=s[10]=10)
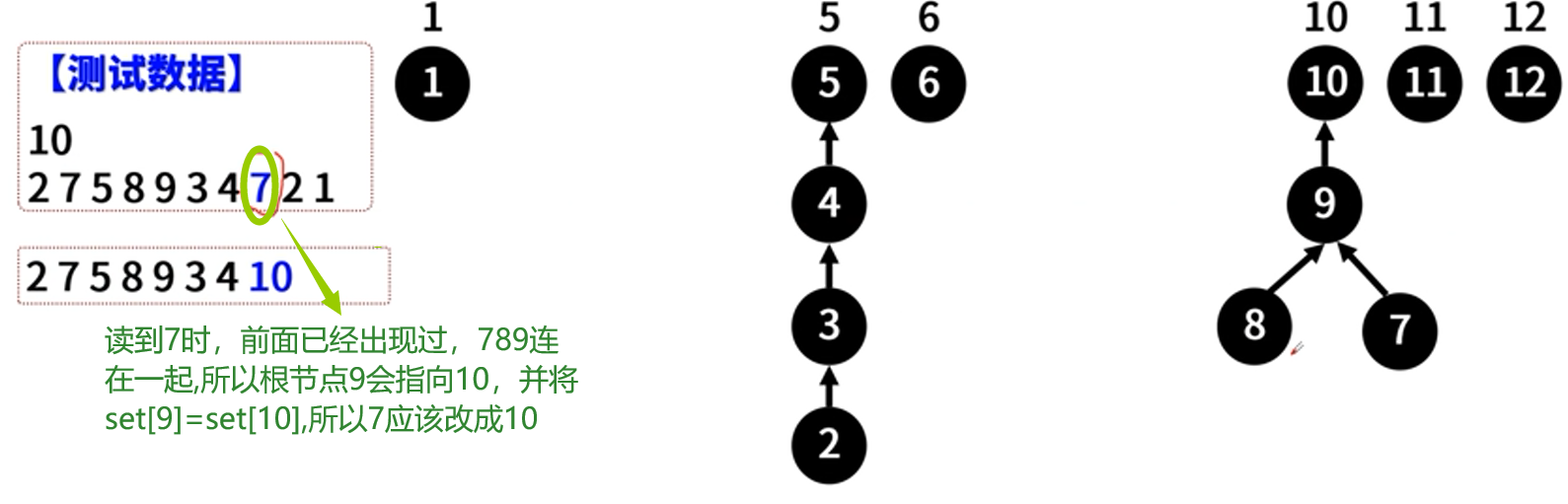
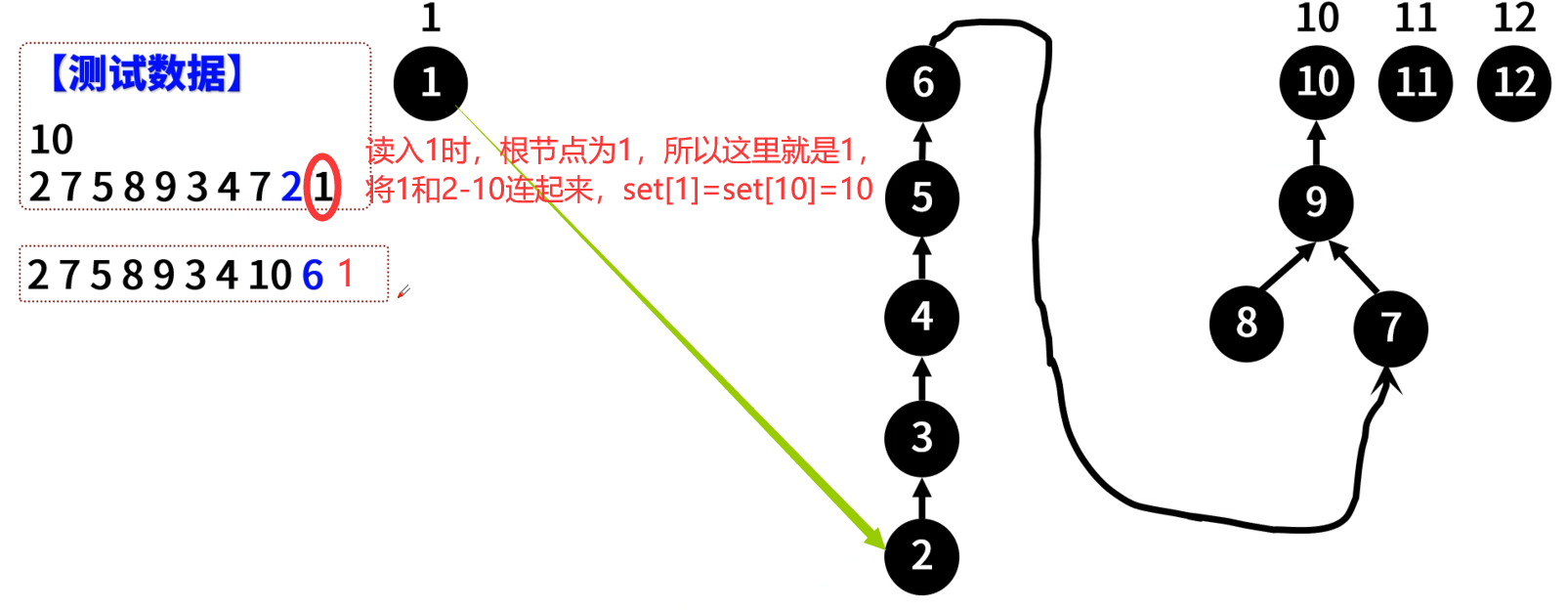
【图解思路】
用并查集s[i]表示访问到i这个数时应该将它换成的数字。以A={6,6,6,6,6}为例。初始化set[i] =i。

图(1)读第一个数A[0]=6。6的集set[6]=6。因为6已经用过了,所以更新set[6]= set[7]=7,作用是后面再读到某个A[k]=6时,可以直接赋值A[k] = set[6]=7。
图(2)读第二个数A[1]=6。6的集set[6]=7,更新A[1]=7。紧接着更新set[7] = set[8]=8。如果后面再读到A[k]=6或7时,可以直接赋值A[k] = set[6]=8或者A[k]=set[7]=8。
图(3)读第三个数A[2]=6。6的集set[6]=8,更新A[2]=8。紧接着更新set[8] = set[9]=9。如果后面再读到A[k]=7或8时,可以直接赋值A[k] = set[7]=9或者A[k]=set[8]=9。
只用到并查集的查询,没用到合并。
必须是“路径压缩”优化的,才能加快查询速度。没有路径压缩的并查集,仍然超时。
复杂度O(n)
【代码】
def find_set(x): #有路径压缩优化的查询
if x != s[x]: s[x] = find_set(s[x])
return s[x]
N=1000002 # 数据规模大一点
s = list(range(N)) #并查集,定义、初始化 s=[0,1,2,3,……]
n = int (input ())
a = [int(i) for i in input ().split()]
for i in range(n) :
root = find_set(a[i]) # 查找到该根节点的集合
a[i] = root # 将根节点赋值给a[i]
s[root] = find_set(root+1) # 这个根节点的集合用过了,s[root]更新为下一个集合:s[root+1]
for i in a: print(i, end = ' ')复杂度:O(n) ,可以通过100%测试
真题训练3:七段码
七段码2020年第十一届蓝桥杯省赛,填空题,lanqiao0J题号595
【问题描述】
七段数码管,一共有7个发光二极管,问能表示多少种不同的字符,要求发光的二极管是相连的。
【思路】
连通性检查可以用DFS、BFS和并查集来做
标准思路:“灯的组合+连通性检查”
编码:“DFS + 并查集”
- a b c d e f g字符用数字表示1 2 3 4 5 6 7
- 灯的所有组合用DFS得到,用“自写组合算法”。
- 选或不选第k个灯,就实现了各种组合。
- check( )函数判断一种组合的连通性。
- 连通性检查用并查集。
- 判断灯i、j都在组合中且相连,那么合并到一个并查集。
def init():
for i in range(N):
s[i]=i
def find_set(x):
if x != s[x]: s[x] = find_set(s[x])
return s[x]
def merge_set(x,y):
x = find_set(x)
y = find_set(y)
if x != y:s[x] = s[y]
def check():
global ans
init()
for i in range(1,8):
for j in range(1,8):
if e[i][j]==1 and vis[i]==1 and vis[j]==1:
merge_set(i,j)
flag = 0
for j in range (1,8):
if vis[j]==1 and s[j]==j: flag +=1
if flag==1:
ans += 1
def dfs (k):#深搜到第k个灯
if k == 8:check()#检查连通性
else:
vis[k] = 1 #点亮这个灯
dfs(k + 1) #继续搜下一个灯
vis[k] = 0 #关闭这个灯
dfs(k + 1)#继续搜下一个灯
N= 10
e=[[0]*N for i in range(N)]
s=[0]*N
vis=[0]*N
ans = 0
e[1][2] = e[1][6]= 1
e[2][1] = e[2][3] = e[2][7]=1
e[3][2] = e[3][4] = e[3][7]= 1
e[4][3] = e[4][5]= 1
e[5][4] = e[5][6] = e[5][7]= 1
e[6][1] = e[6][5] = e[6][7]= 1
e[7][2] = e[7][3] = e[7][5] = e[7][6]= 1
dfs (1) #从第一个灯开始深搜
print(ans)