目录
开篇引言
题目描述
代码实现
题目拓展
拓展解读
一类
100. 相同的树
226. 翻转二叉树
104. 二叉树的最大深度
110. 平衡二叉树
543. 二叉树的直径
617. 合并二叉树
572. 另一个树的子树
965. 单值二叉树
二类
101. 对称二叉树
解题总结
开篇引言
力扣上很多树的题目都是可以用递归很快地解决的,而这一系列递归解法中蕴含了一种很强大的递归思维:对称性递归(symmetric recursion) 什么是对称性递归?就是对一个对称的数据结构(这里指二叉树)从整体的对称性思考,把大问题分解成子问题进行递归,即不是单独考虑一部分(比如树的左子树),而是同时考虑对称的两部分(左右子树),从而写出对称性的递归代码。
题目描述
输入两棵二叉树A和B,判断B是不是A的子结构。(约定空树不是任意一个树的子结构)
B是A的子结构, 即 A中有出现和B相同的结构和节点值。
例如:
给定的树 A:
3
/ \
4 5
/ \
1 2
给定的树 B:
4
/
1
返回 true,因为 B 与 A 的一个子树拥有相同的结构和节点值。
示例 1:
输入:A = [1,2,3], B = [3,1] 输出:false
示例 2:
输入:A = [3,4,5,1,2], B = [4,1] 输出:true
代码实现
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode(int x) { val = x; }
* }
*/
class Solution {
/*
* 死死记住isSubStructure()的定义:判断B是否为A的子结构
*/
public boolean isSubStructure(TreeNode A, TreeNode B) {
// 若A与B其中一个为空,立即返回false
if(A == null || B == null) {
return false;
}
// B为A的子结构有3种情况,满足任意一种即可:
// 1.B的子结构起点为A的根节点,此时结果为recur(A,B)
// 2.B的子结构起点隐藏在A的左子树中,而不是直接为A的根节点,此时结果为isSubStructure(A.left, B)
// 3.B的子结构起点隐藏在A的右子树中,此时结果为isSubStructure(A.right, B)
return recur(A, B) || isSubStructure(A.left, B) || isSubStructure(A.right, B);
}
/*
判断B是否为A的子结构,其中B子结构的起点为A的根节点
*/
private boolean recur(TreeNode A, TreeNode B) {
// 若B走完了,说明查找完毕,B为A的子结构
if(B == null) {
return true;
}
// 若B不为空并且A为空或者A与B的值不相等,直接可以判断B不是A的子结构
if(A == null || A.val != B.val) {
return false;
}
// 当A与B当前节点值相等,若要判断B为A的子结构
// 还需要判断B的左子树是否为A左子树的子结构 && B的右子树是否为A右子树的子结构
// 若两者都满足就说明B是A的子结构,并且该子结构以A根节点为起点
return recur(A.left, B.left) && recur(A.right, B.right);
}
}题目拓展
可以用对称性递归解决的二叉树问题大多是判断性问题(bool类型函数),这一类问题又可以分为以下两类:
1、不需要构造辅助函数。这一类题目有两种情况:第一种是单树问题,且不需要用到子树的某一部分(比如根节点左子树的右子树),只要利用根节点左右子树的对称性即可进行递归。第二种是双树问题,即本身题目要求比较两棵树,那么不需要构造新函数。该类型题目如下:
100. 相同的树
226. 翻转二叉树
104. 二叉树的最大深度
110. 平衡二叉树
543. 二叉树的直径
617. 合并二叉树
572. 另一个树的子树
965. 单值二叉树
2、需要构造辅助函数。这类题目通常只用根节点子树对称性无法完全解决问题,必须要用到子树的某一部分进行递归,即要调用辅助函数比较两个部分子树。形式上主函数参数列表只有一个根节点,辅助函数参数列表有两个节点。该类型题目如下:
101. 对称二叉树
剑指 Offer 26. 树的子结构
拓展解读
一类
100. 相同的树
public boolean isSameTree(TreeNode p, TreeNode q) {
if(p==q && p==null){
return true;
}
if(p==null && q!=null){
return false;
}
if(p!=null && q==null){
return false;
}
TreeNode lleft = p.left;
TreeNode lright = p.right;
TreeNode rleft = q.left;
TreeNode rright = q.right;
if(p.val!=q.val){
return false;
}
return isSameTree(lleft,rleft) && isSameTree(lright,rright);
}226. 翻转二叉树
public TreeNode invertTree(TreeNode root) {
if(root==null) {
return null;
}
//下面三句是将当前节点的左右子树交换
TreeNode tmp = root.right;
root.right = root.left;
root.left = tmp;
invertTree(root.left);
invertTree(root.right);
return root;
}104. 二叉树的最大深度
public int maxDepth(TreeNode root) {
int leftDepth = 0;
int rightDepth = 0;
if(root==null){
return 0;
}
if(root.left==null && root.right==null){
return 1;
}
if(root.left!=null){
leftDepth = maxDepth(root.left)+1;
}
if(root.right!=null){
rightDepth = maxDepth(root.right)+1;
}
return Math.max(leftDepth,rightDepth);
}
110. 平衡二叉树
public boolean isBalanced(TreeNode root) {
if(root==null){
return true;
}
return Math.abs(getHeght(root.left)-getHeght(root.right))<2 && isBalanced(root.left) && isBalanced(root.right);
}
public int getHeght(TreeNode root){
if(root==null){
return 0;
}
return Math.max(getHeght(root.left),getHeght(root.right))+1;
}543. 二叉树的直径
int diameter;
public int diameterOfBinaryTree(TreeNode root) {
diameter = 0;
traverse(root);
return diameter;
}
// 返回树的深度
int traverse(TreeNode root) {
if (root == null) {
return 0;
}
int left = traverse(root.left); // 左子树的深度
int right = traverse(root.right); // 右子树的深度
// 直接访问全局变量
diameter = Math.max(diameter, left + right);
return 1 + Math.max(left, right);
}
在这道题中,全局变量计算的是路径的最大值(max)。计算 max 的方式不是一次性求出来的,而是在二叉树遍历的过程中,每出现一个值,就把这个值和全局变量比较计算,算一个最大值。最终全局变量能得到全局的最大值。
实际上这利用了 max 的性质,max 是一种在线算法。简单来说,在线算法就是在计算的时候,所有的输入数据以“流”的形式一个个进来,算法每次只处理一条数据,不需要保存全部的数据。
除了 max 之外,sum、all 也都属于在线算法(all 指的是 x1 && x2 && ... && xn 这样的计算)。可以举几个其他的二叉树题目例子:
二叉树的坡度:563. Binary Tree Tilt(sum)
public int findTilt(TreeNode root) {
if(root==null){
return 0;
}
int leftSum = getSum(root.left);
int rightSum = getSum(root.right);
root.val= Math.abs(leftSum -rightSum);
return root.val + findTilt(root.left) + findTilt(root.right);
}
public int getSum(TreeNode root){
if(root==null){
return 0;
}
return root.val + getSum(root.left) + getSum(root.right);
}判断平衡二叉树:110. Balanced Binary Tree(all)
二叉树路径数字:129. Sum Root to Leaf Numbers(sum)
617. 合并二叉树
把root1作为返回树
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
if(root1==null && root2==null){
return root1;
}else if((root1==null && root2!=null) || (root1!=null && root2==null)){
if(root1==null){
root1 =new TreeNode(root2.val);
root1.left = mergeTrees(null,root2.left);
root1.right = mergeTrees(null,root2.right);
}else{
root1.left = mergeTrees(root1.left,null);
root1.right = mergeTrees(root1.right,null);
}
}else{
root1.val= root1.val + root2.val;
root1.left = mergeTrees(root1.left,root2.left);
root1.right = mergeTrees(root1.right,root2.right);
}
return root1;
}返回一个新的树,可以简化代码
public TreeNode mergeTrees(TreeNode t1, TreeNode t2) {
if (t1 == null) {
return t2;
}
if (t2 == null) {
return t1;
}
TreeNode merged = new TreeNode(t1.val + t2.val);
merged.left = mergeTrees(t1.left, t2.left);
merged.right = mergeTrees(t1.right, t2.right);
return merged;
}
572. 另一个树的子树
注意子树和子结构的区别:
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。
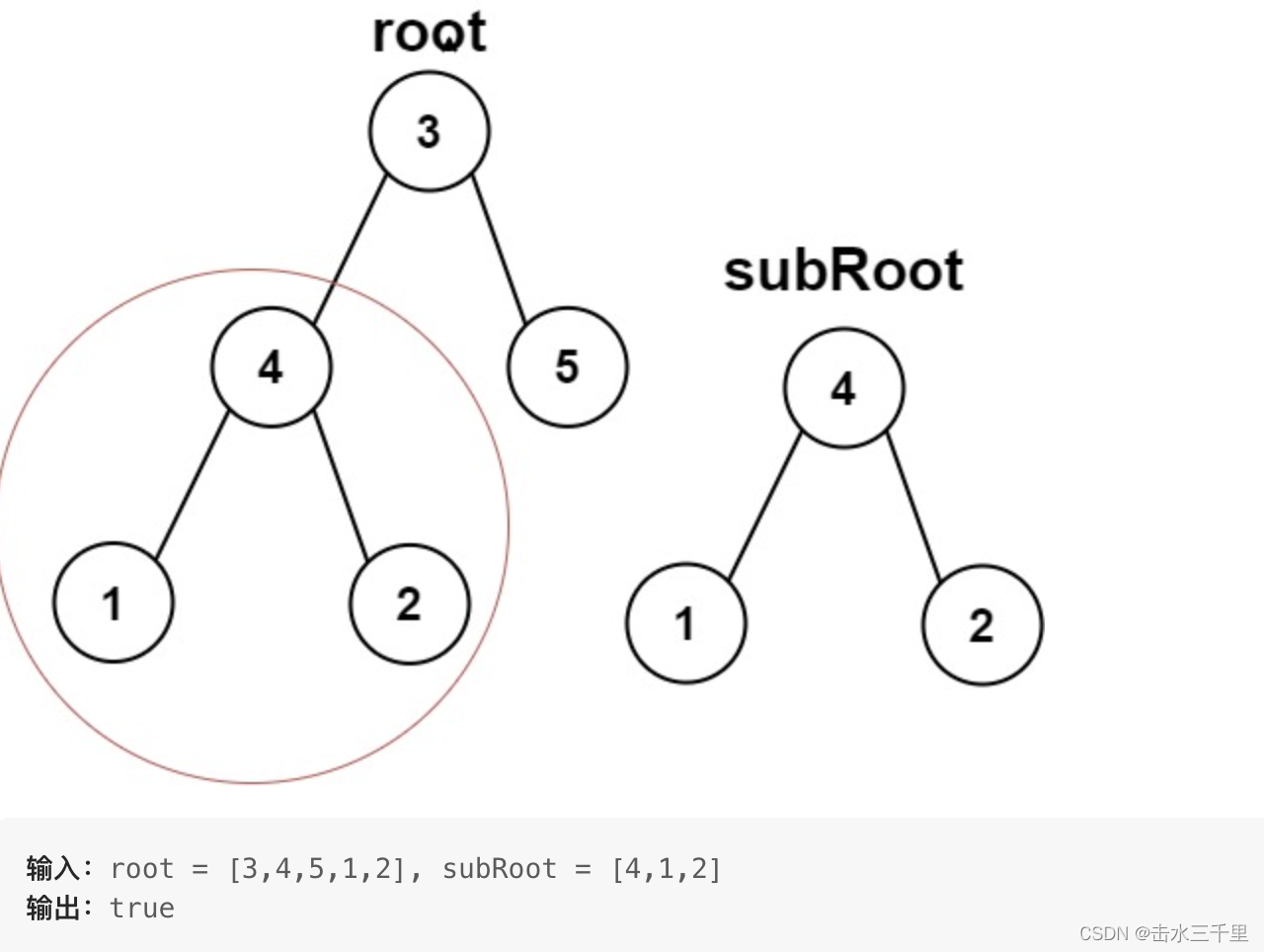
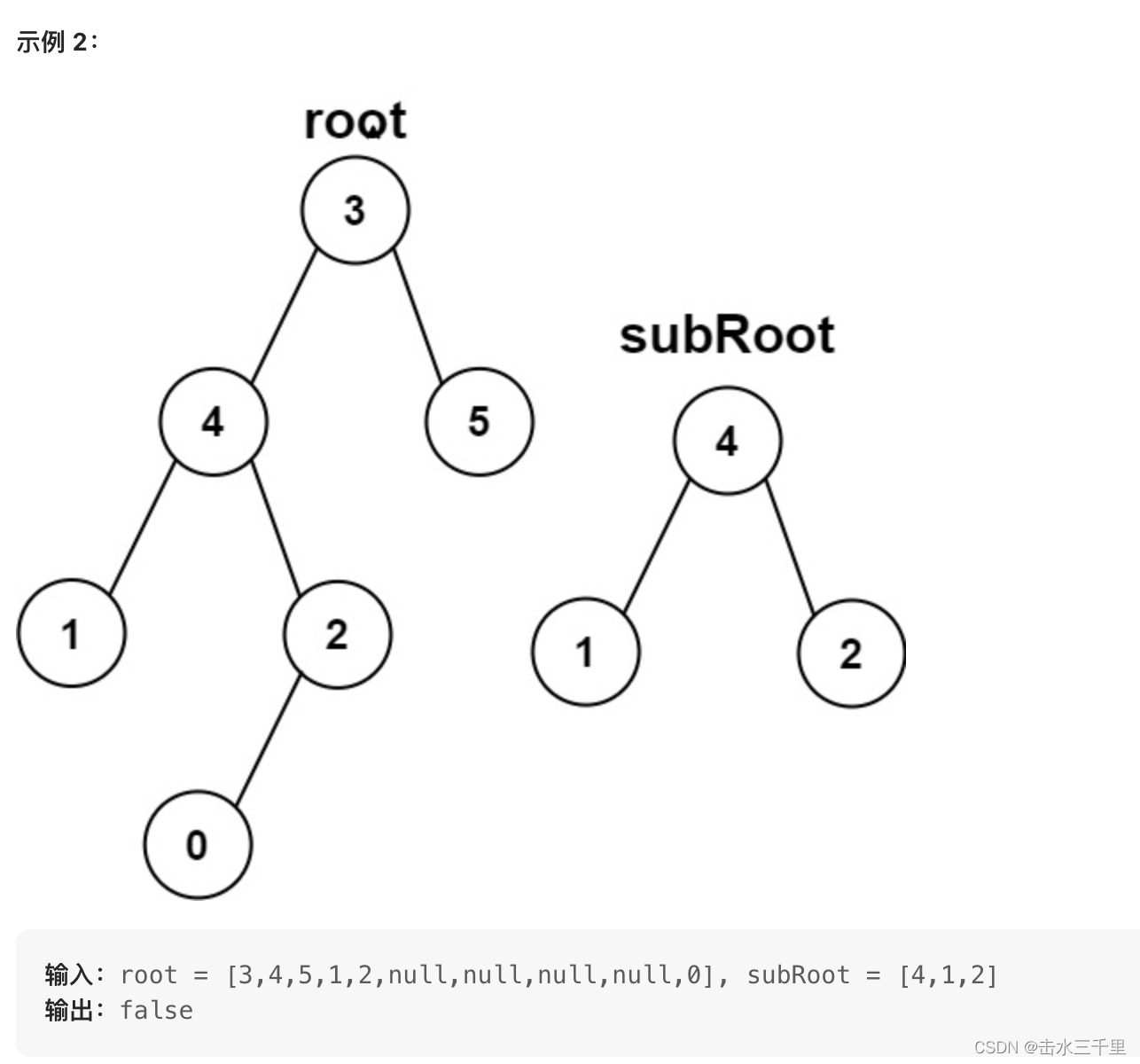
代码可以在本文主题目的基础上删稍作修改就可以使用
965. 单值二叉树
int univalVal=-1;
public boolean isUnivalTree(TreeNode root) {
Boolean flag = true;
if(root!=null){
if(univalVal==-1){
univalVal = root.val;
}
if(root.val!=univalVal){
flag =false;
}
return flag && isUnivalTree(root.left) && isUnivalTree(root.right);
}
return true;
}二类
101. 对称二叉树
public boolean isSymmetric(TreeNode root) {
if(root==null) {
return true;
}
//调用递归函数,比较左节点,右节点
return dfs(root.left,root.right);
}
boolean dfs(TreeNode left, TreeNode right) {
//递归的终止条件是两个节点都为空
//或者两个节点中有一个为空
//或者两个节点的值不相等
if(left==null && right==null) {
return true;
}
if(left==null || right==null) {
return false;
}
if(left.val!=right.val) {
return false;
}
//再递归的比较 左节点的左孩子 和 右节点的右孩子
//以及比较 左节点的右孩子 和 右节点的左孩子
return dfs(left.left,right.right) && dfs(left.right,right.left);
}解题总结
- 一般来说思维越奇特代码越简洁,官方题解一般代表了“最优代码”,普通的思维不一定可以马上领会,可以退而求其次再优化“思维”简化代码。
- 在练习中插入两个以上的主题或技能,也是一种胜过集中练习的学 习方法
- 与集中练习相比,穿插练习与多样化练习的一个显著优点是,它们有助于我们更好地学习如何评估背景,以及辨识问题间的差异,从一系列可选的答案中选择并应用正确的解决方案。
- 人们顽固地相信,自己把心思放在一件事上,拼命重复就能学得更好,认为这些观点经受住了时间的考验,而且“练习,练习,再练习”的明显收效再次证明了这种方法的好处。但是,科学家们把习得技能阶段的这种成绩称为“暂时的优势”,并把它同“潜在的习惯优势”区分开来。形成习惯优势有种种技巧,例如有间隔的练习、有穿插内容的练习,引出努力的动力。 及多样化练习,这些技巧恰恰会放缓有明显成果的学习进程,它们不会在练习中提高我们的表现。我们从表面上看不到成绩提高,也就没有付出的动力
- 心智模型可以 被调整,可以在复杂多变的环境中发挥作用。专业的表现,源自在不同
环境下、在专长领域进行的数千小时的练习。通过这些练习,你可以积 累大量类似的心智模型,从而保证自己在特定环境下做出正确分析,立 刻挑选出正确的应对方案并加以执行。