一、判断线段是否相交需要下面两步：

（1）快速排斥实验
（2）跨立实验

二、第一步快速排斥实验

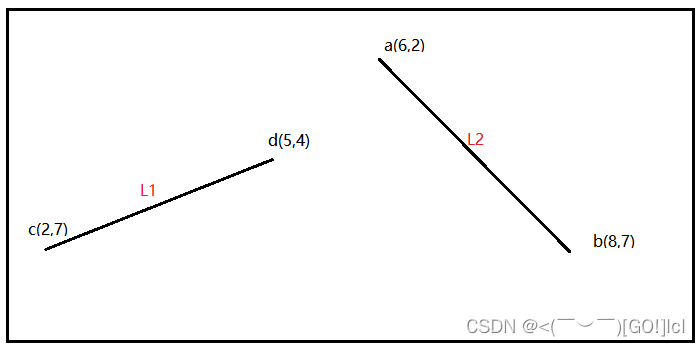
在这里插入图片描述
对上图两条L1,L2线段来说，L1 x的最大值为d端点x=5，L2 x的最小值为a端点x=6，这就说明这两条线段肯定没有相交。
其他情况类似，代码表示如下：

max(C.x,D.x)<min(A.x,B.x) || max(C.y,D.y)<min(A.y,B.y) ||
max(A.x,B.x)<min(C.x,D.x) || max(A.y,B.y)<min(C.y,C.y)

如果上面的四条判断有一个为真，则代表两条线段不相交；否则进行第二步判断。

三、第二步跨立实验

1、向量叉乘的几何意义

（1）二维向量叉乘公式
二维向量叉乘公式a（x1，y1），b（x2，y2），则a×b＝（x1y2－x2y1），不需要证明的就是定义的运算。三维叉乘是行列式运算，也是叉积的定义，你把第三维看做0代入就行了。
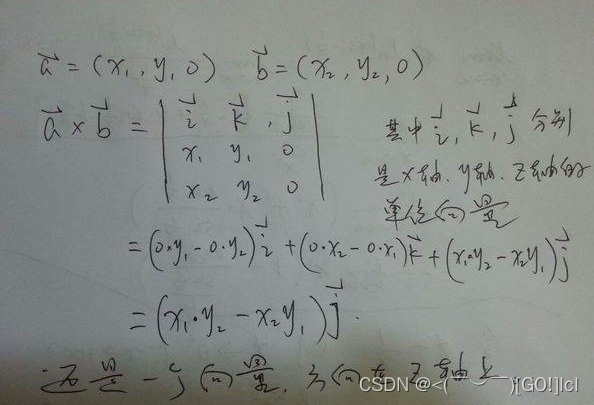
在这里插入图片描述
（2）叉积与线段方向关系
两个坐标A(x1,y1),B(x2,y2),那么AxB的向量积就是x1y2-y1x2。
我们假定一个向量积R，R=x1y2-y1x2。
R<0 说明A在B的逆时针方向。
R=0 说明A与B共线，可能正向也可能反向。
R>0 说明A在B的顺时针方向。

2、举例说明

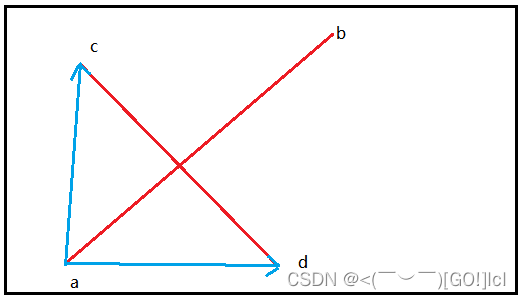
证明两条线段相交就要证明两条线段相互跨立，如果两条线段相交，那么一条线段两边的两个点要位于另一条线段的两边。
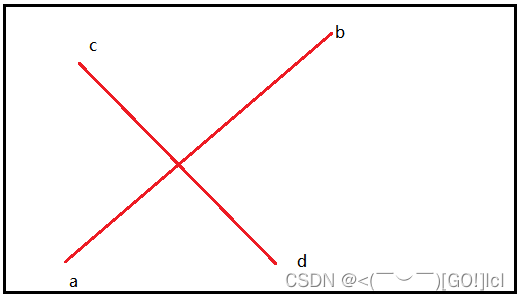
在这里插入图片描述
相交的情况下，我们从a点出发，分别沿ac，ad方向，得到两个向量，可以得到R>0;

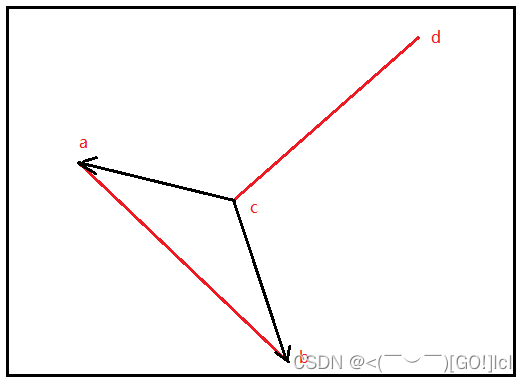
不相交的情况下，我们从c点出发，分别沿ca，cb方向，得到两个向量，可以得到R<0;

代码表示如下：

struct Line {
    double x1;
    double y1;
    double x2;
    double y2;
};
 
bool intersection(const Line &l1, const Line &l2)
{
    //快速排斥实验
    if ((l1.x1 > l1.x2 ? l1.x1 : l1.x2) < (l2.x1 < l2.x2 ? l2.x1 : l2.x2) ||
        (l1.y1 > l1.y2 ? l1.y1 : l1.y2) < (l2.y1 < l2.y2 ? l2.y1 : l2.y2) ||
        (l2.x1 > l2.x2 ? l2.x1 : l2.x2) < (l1.x1 < l1.x2 ? l1.x1 : l1.x2) ||
        (l2.y1 > l2.y2 ? l2.y1 : l2.y2) < (l1.y1 < l1.y2 ? l1.y1 : l1.y2))
    {
        return false;
    }
    //跨立实验
    if ((((l1.x1 - l2.x1)*(l2.y2 - l2.y1) - (l1.y1 - l2.y1)*(l2.x2 - l2.x1))*
        ((l1.x2 - l2.x1)*(l2.y2 - l2.y1) - (l1.y2 - l2.y1)*(l2.x2 - l2.x1))) > 0 ||
        (((l2.x1 - l1.x1)*(l1.y2 - l1.y1) - (l2.y1 - l1.y1)*(l1.x2 - l1.x1))*
        ((l2.x2 - l1.x1)*(l1.y2 - l1.y1) - (l2.y2 - l1.y1)*(l1.x2 - l1.x1))) > 0)
    {
        return false;
    }
    return true;
}