【机器学习300问】39、高斯分布模型如何实现异常检测？

news2024/11/24 0:39:32

一、异常检测是什么？

（1）举几个例子

① 信用卡交易异常检测

在信用卡交易数据分析中，如果某个用户的消费习惯通常是小额且本地化消费，那么突然出现一笔大额且跨国的交易就可能被标记为异常。

② 电机温度异常检测

在电机运行数据分析中，如果一台电机的历史温度数据显示其在正常负载和冷却条件下通常保持在一个稳定的中低温区间，那么突然出现一次大幅度升温或高温持续不退的现象，会被标记为潜在的异常情况，可能预示着电机存在过载、散热不良或其他机械故障的风险。

（2）异常检测的定义

异常检测指的是识别并标记那些显著偏离常规模式或预期行为的数据点的过程。它关注的是找出与大多数数据显著不同的个体或事件。异常检测通常应用于安全监控、故障预测、信用欺诈检测等诸多场景中，它的目标不是划分数据，而是找出潜在的异常现象。

二、高斯分布的基本知识

（1）高斯分布是什么？

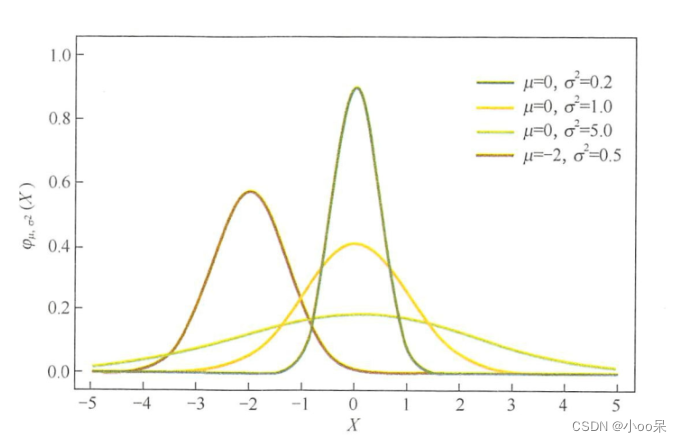
高斯分布（Gaussian distribution），也称为正态分布（Normal distribution），是一种连续概率分布，高斯分布的图形是对称的，关于均值μ对称，当μ=0且σ=1时，分布被称为标准正态分布。如果我们有一组数 $x_1, x_2, \dots, x_n$

均值（ $\mu$ ）：高斯分布的中心点，也是数据集的平均值，所有观测值围绕此点集中分布。

$\mu = \frac{1}{n}\sum_{i=1}^{n}x_i$

标准差（ $\sigma$ ）：衡量数据相对于均值分散的程度。

$\sigma = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2}$

方差（ $\sigma ^2$ ）：是各个数据点与它们的平均数（均值）差的平方的平均数。

$\sigma ^2 = \frac{1}{n}\sum_{i=1}^{n}(x_i - \mu)^2$

高斯分布的重要性质在于它在自然界和社会科学中的普遍适用性，很多随机过程在一定条件下都会趋向于高斯分布，这被称为中心极限定理。

【注】机器学习中方差通常除以n而非统计学中的n-1。在实际使用中区别很小，几乎可以忽略不计。在机器学习领域大部分人更习惯使用n-1。

（2）它的概率密度函数长什么样？

高斯分布的概率密度函数是一个关于变量x的函数公式为：

$p(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi\sigma^2}} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$

其中 $x$ 是随机变量， $\mu$ 是期望值（均值） $\sigma ^2$ 是方差， $\sigma$ 是标准差。

（3）什么是多维高斯分布？

多维高斯分布（Multivariate Gaussian Distribution），也称为多元正态分布或多变量正态分布，是一种在多维空间中的概率分布模型，它扩展了一维正态分布的概念到多个变量的情况。在多维空间中，每个观察数据点都是一个向量而不是单个数值。概率密度函数（Probability Density Function, PDF）公式如下：

$p(\mathbf{x}; \boldsymbol{\mu}, \mathbf{\Sigma}) = \frac{1}{\sqrt{(2\pi)^d |\mathbf{\Sigma}|}} \exp\left(-\frac{1}{2}(\mathbf{x} - \boldsymbol{\mu})^\top \mathbf{\Sigma}^{-1} (\mathbf{x} - \boldsymbol{\mu})\right)$

假设我们正在研究一所大学新生入学考试成绩的数据，其中包括了数学（Math）和英语（English）两门科目的成绩。我们可以假设这些成绩整体上服从多维高斯分布。如果新录取的一名学生的成绩向量为 $X_{new}=[x_m,x_e]$ ，我们可以通过多维高斯分布计算出这个成绩向量的概率密度函数值，然后与预设的阈值比较，以判断这个成绩组合是否异常，即是否显著偏离大部分学生的成绩分布。

多维高斯分布的特点是其概率密度函数呈现出一个椭球状的分布形态，其中椭球的中心对应均值向量，椭球的形状和方向由协方差矩阵决定。

三、高斯分布模型

在实际应用中，高斯分布（正态分布）常被用来开发异常检测算法，尤其是在一维或多维连续数据中。这种情况下，假设数据服从高斯分布（这里埋个坑后续出个文章讲讲为什么要假设符合高斯分布？以及万一数据不符合高斯分布该怎么办呢？），我们可以基于高斯分布的概率密度函数（PDF）来评估数据点的“正常”程度。

（1）高斯分布异常检测算法

利用高斯分布模型来解决异常检测问题，对于给定的数据集 $x_1, x_2, \dots, x_m$ 针对每一个特征计算出 $\mu$ 和 $\sigma^2$ 的估计值：

$\mu_j = \frac{1}{m}\sum_{i=1}^{m}x_j^{(i)}$

$\sigma ^2_j = \frac{1}{m}\sum_{i=1}^{m}(x_j^{(i)} - \mu_j)^2$

模型的公式为：

$p(x)=\prod_{j=1}^{n}p(x_j|\mu_j,\sigma_j^2)=\prod_{j=1}^{n}\frac{1}{\sqrt{2\pi }\sigma_j}e^{-\frac{(x_j-\mu_j)^2}{2\sigma_j^2}}$

根据训练集中的样本点计算出了均值和方差后就拟合得到了模型 $p(x)$ （其实就是PDF），然后你如果给定新的一个样本点 $x_{new}$ ，想知道它到底是不是异常的样本数据，就可以把它带入公式计算 $p(x_{new})$ ，当 $p(x_{new})< \varepsilon$ 时说明是异常的数据。