在Matlab中,inv()函数是用来求解矩阵的逆矩阵的函数。逆矩阵是一个与原矩阵相乘后得到单位矩阵的矩阵。在数学中,矩阵A的逆矩阵通常用A^-1表示。
什么是逆矩阵
在数学中,对于一个n阶方阵A,如果存在一个n阶方阵B,使得AB=BA=I(单位矩阵),那么B就是A的逆矩阵,记为A^-1。只有非奇异(可逆)的方阵才有逆矩阵。
逆矩阵的性质如下:
- 若A可逆,则A^-1也可逆,并且(A^-1)^-1 = A
- 若A可逆,则transpose(A)可逆,并且(transpose(A))^-1 = transpose(A^-1)
- 若A和B可逆,则AB也可逆,并且(AB)^-1 = B^-1A^-1
inv()函数调用的注意事项
在调用inv()函数时,需要注意以下几点:
- 输入的矩阵必须是一个方阵,否则会报错。
- 输入的矩阵必须是非奇异的(可逆的),否则会报错。
- 逆矩阵的计算是一个较为复杂和耗时的计算过程,对于大规模的矩阵,可能会耗费较长的时间。
案例:
接下来我们以一个简单案例来描述:
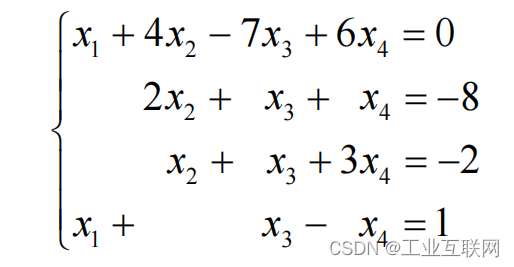
求解以上方程组:
先设
X
=[
x
1
;
x
2
;
x
3
;
x
4
]
为列向量
%矩阵设计
A=[1 4 -7 6;0 2 1 1;0 1 1 3;1 0 1 -1],
B=[0;-8;-2;1],
X=A\B
A
B
X
inv(A)*B

图:结果
根据以上结果,我们可以看出来A\B 与 inv(A)*B 相等。
然后设 X=[x1 x2 x3 x4]为行向量
%矩阵设计
A=[1 0 0 1;4 2 1 0;-7 1 1 1;6 1 3 -1],
B=[0 -8 -2 1],
X=B/A
A
B
X
B*inv(A)
图:结果
由此可见,A/B
的确与
B*inv(A)相等