文章目录
- 回顾
- RNN
- RNN Cell
- RNNCell的使用
- RNN的使用
- RNN例子
- 使用RNN Cell实现
- 使用RNN实现
- 嵌入层 Embedding
- 独热向量的缺点
- Embedding
- LSTM
- GRU(门控循环单元)
- 练习
回顾
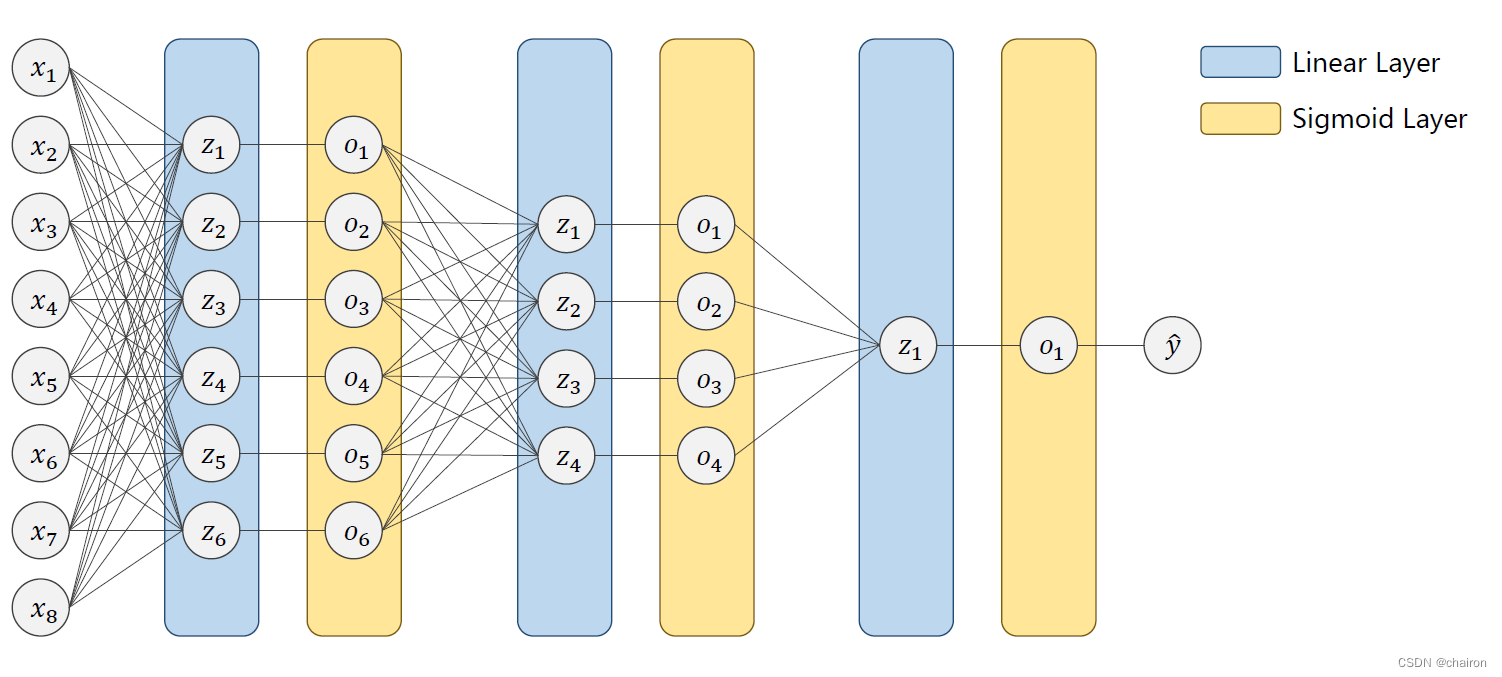
DNN(全连接):和CNN相比,拥有巨大的参数量,CNN权重共享因此参数量小很多。
RNN
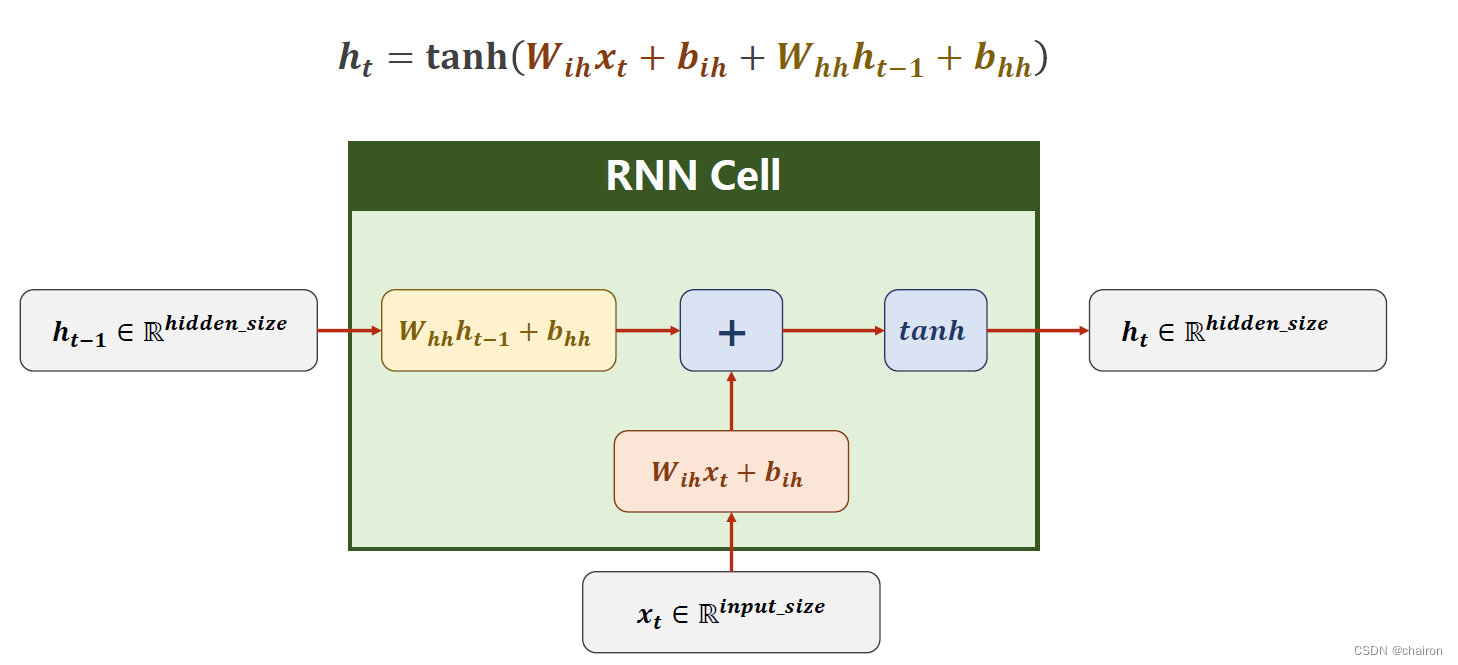
RNN Cell
RNN主要是处理带有时间序列特征的数据(前后文拥有逻辑关系)
- 自然语言:依赖于词的顺序
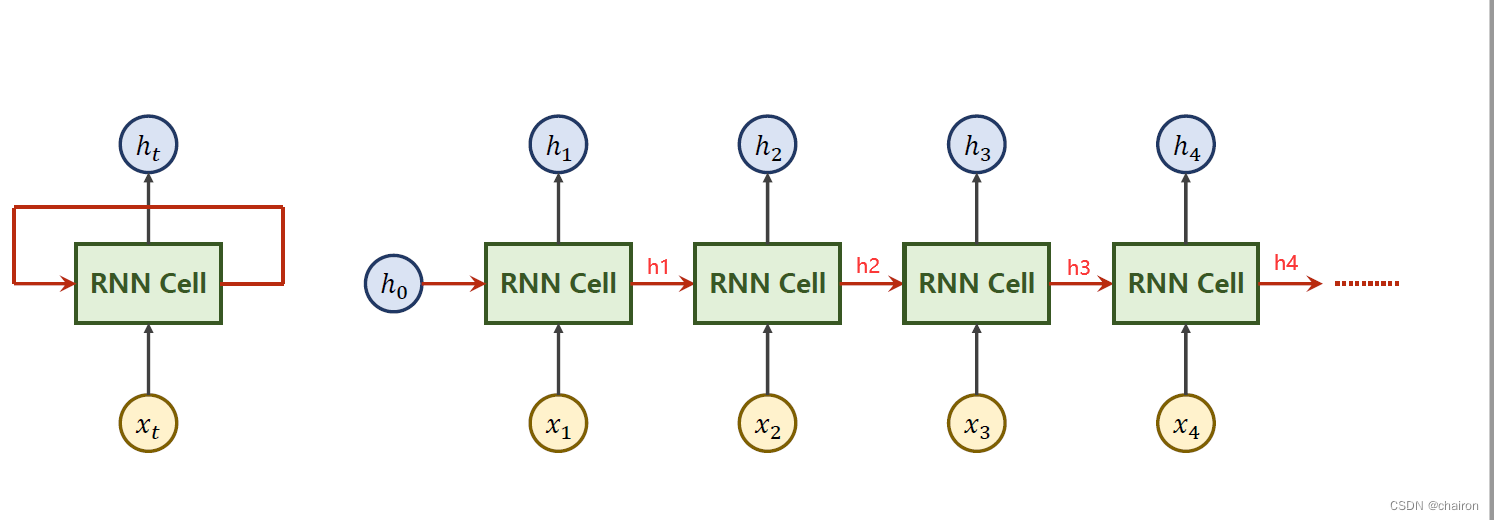
以上的RNN cell为同一个线形层(处理一个序列),其实以上是一个循环:
RNN Cell具体计算过程如下:
RNNCell的使用
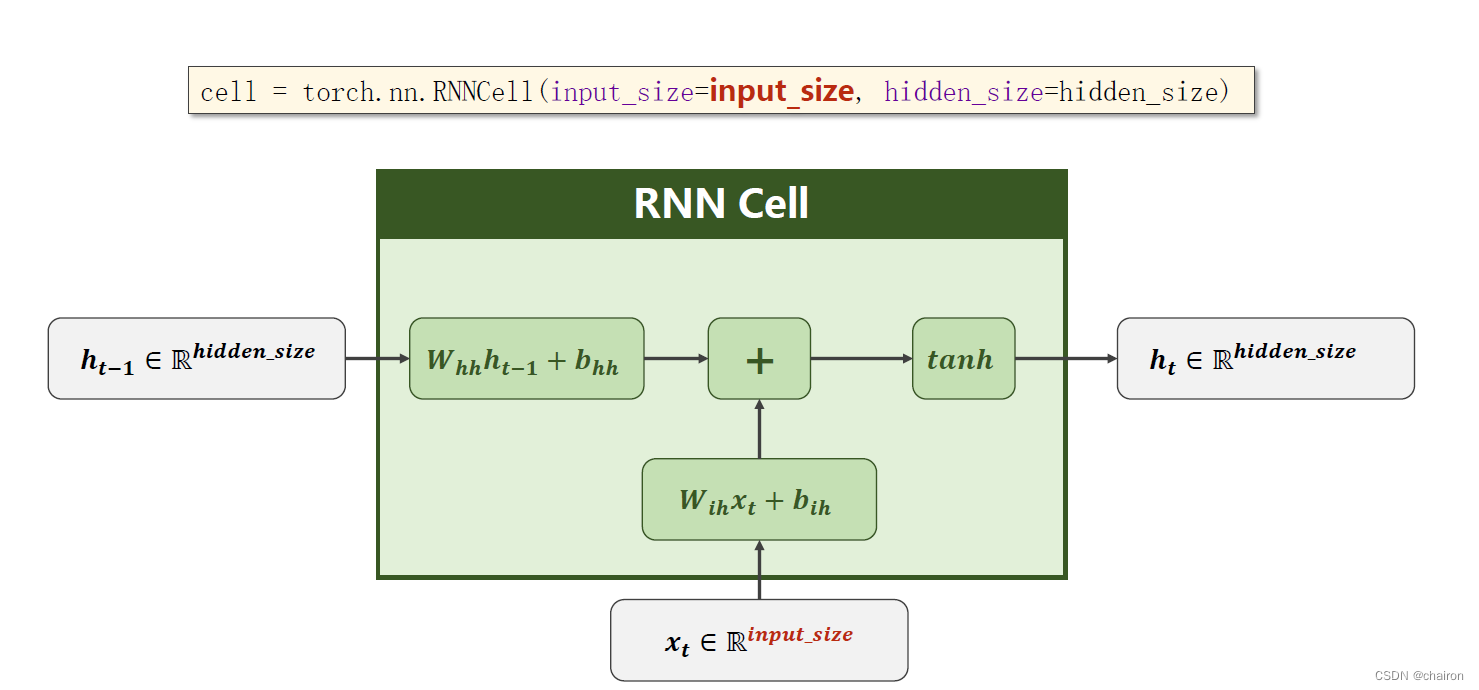

假设有以下这些条件: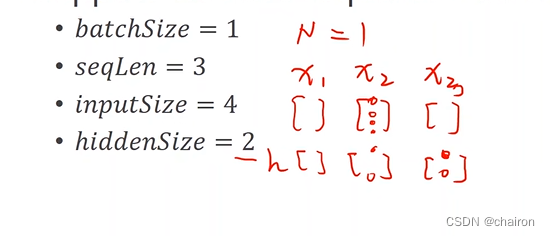
RNNCell的输入、输出的维度就应该是:

数据集的形状应该是:
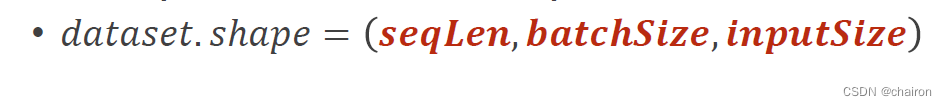
seqLen应该放在最前面,方便循环。
#练习1
import torch
batch_size=1
seq_len=3
input_size=4
hidden_size=2
#构建RNNcell,RNNcell本质是一个Linear层
cell=torch.nn.RNNCell(input_size=input_size,hidden_size=hidden_size)
#(seq,batch,feartures)
#产生形状为(seq_len,batch_size,input_size)的序列
dataset= torch.randn(seq_len,batch_size,input_size)
#初始化hidden为0
hidden =torch.zeros(batch_size,hidden_size)
for idx, input in enumerate (dataset):#遍历datset中的序列
print('='*20,'='*20)
print('Input size:',input.shape)#[1, 4]
hidden=cell(input,hidden)#上一个的output作为下一个的hidden
print('output size:',hidden.shape) #[1, 2],output size=hidden size,上一个的output作为下一个的hidden
print(hidden)
结果:
==================== ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[-0.4549, 0.6699]], grad_fn=<TanhBackward0>)
==================== ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[-0.7693, 0.1919]], grad_fn=<TanhBackward0>)
==================== ====================
Input size: torch.Size([1, 4])
output size: torch.Size([1, 2])
tensor([[0.2945, 0.8171]], grad_fn=<TanhBackward0>)
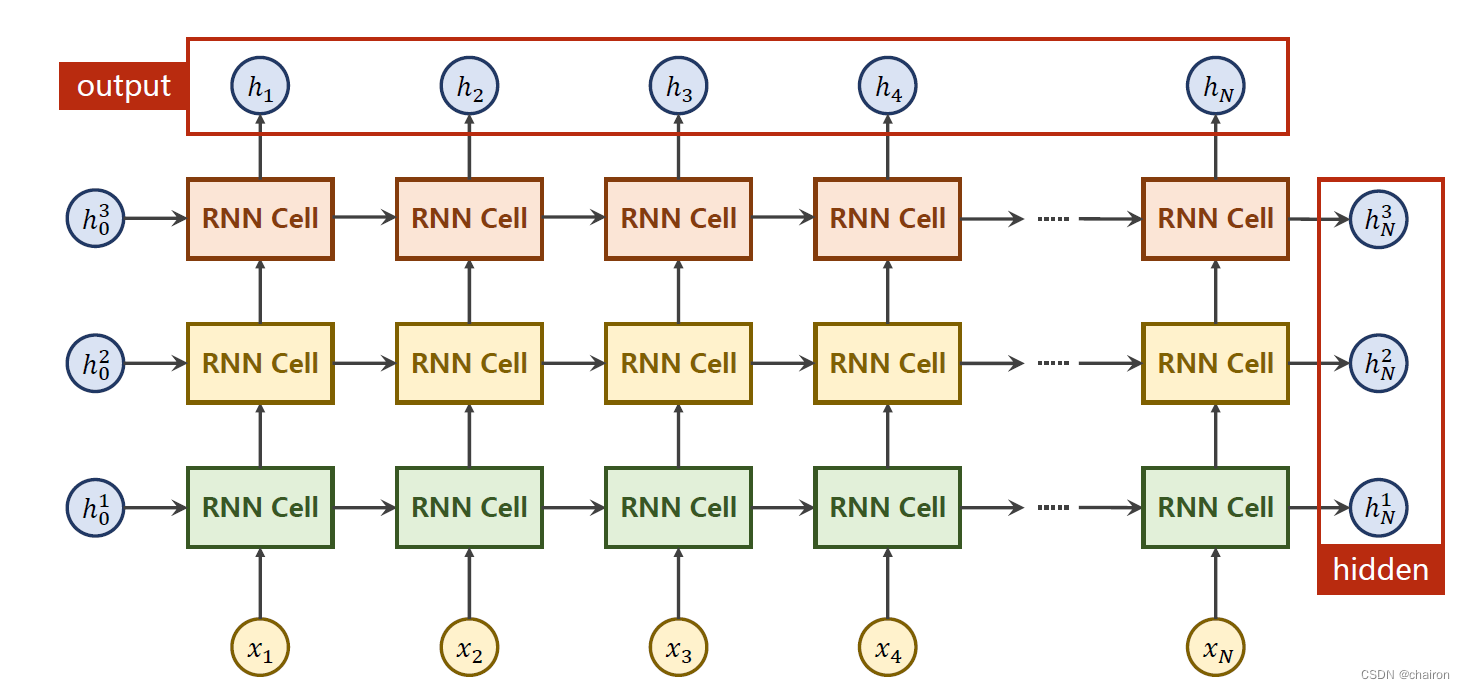
RNN的使用
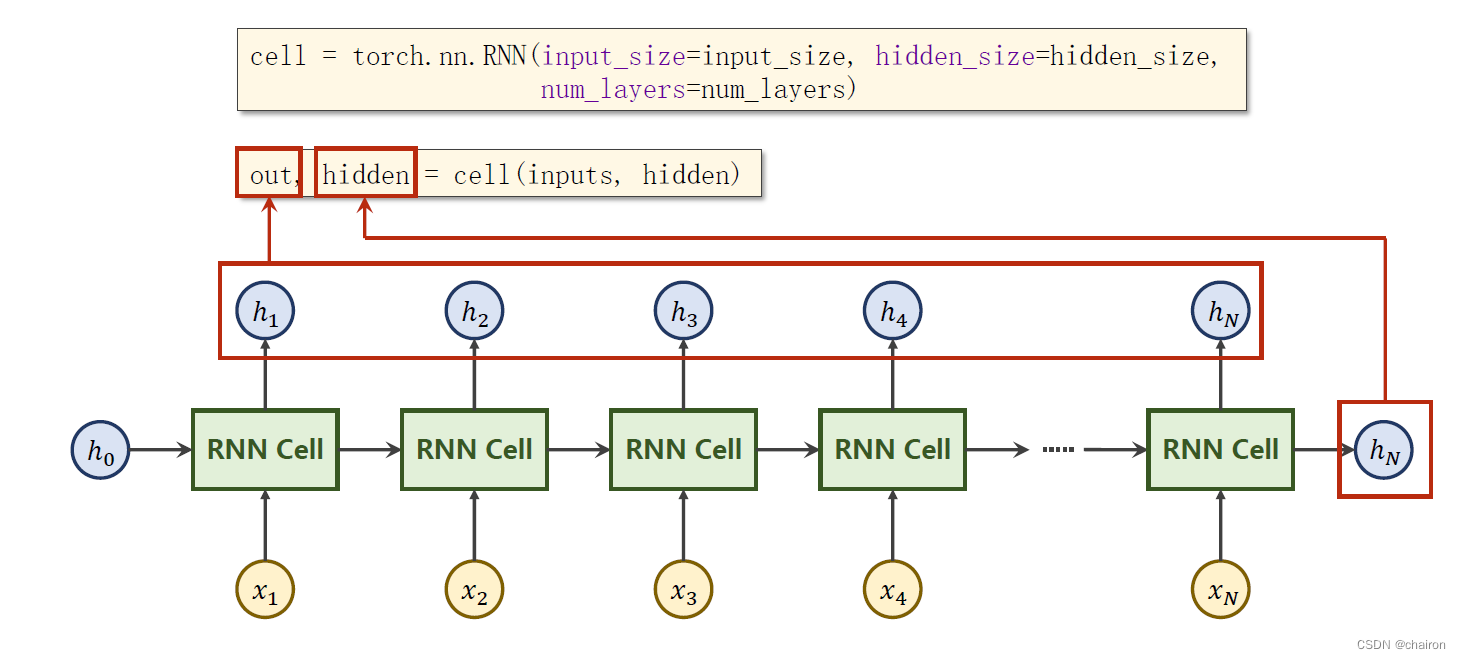
inputs:全部的输入序列;shape=(𝑠𝑒𝑞𝑆𝑖𝑧𝑒,𝑏𝑎𝑡𝑐ℎ,𝑖𝑛𝑝𝑢𝑡_𝑠𝑖𝑧𝑒)
out:全部的隐层输出;shape=(𝑠𝑒𝑞𝐿𝑒𝑛,𝑏𝑎𝑡𝑐ℎ,ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒)
hidden:最后一层的隐层输出;shape=(𝑛𝑢𝑚𝐿𝑎𝑦𝑒𝑟𝑠,𝑏𝑎𝑡𝑐ℎ,ℎ𝑖𝑑𝑑𝑒𝑛_𝑠𝑖𝑧𝑒)
需要的参数:
• 𝑏𝑎𝑡𝑐ℎ𝑆𝑖𝑧𝑒
• 𝑠𝑒𝑞𝐿𝑒𝑛
• 𝑖𝑛𝑝𝑢𝑡𝑆𝑖𝑧𝑒,ℎ𝑖𝑑𝑑𝑒𝑛𝑆𝑖𝑧𝑒,
• 𝑛𝑢𝑚𝐿𝑎𝑦𝑒𝑟𝑠
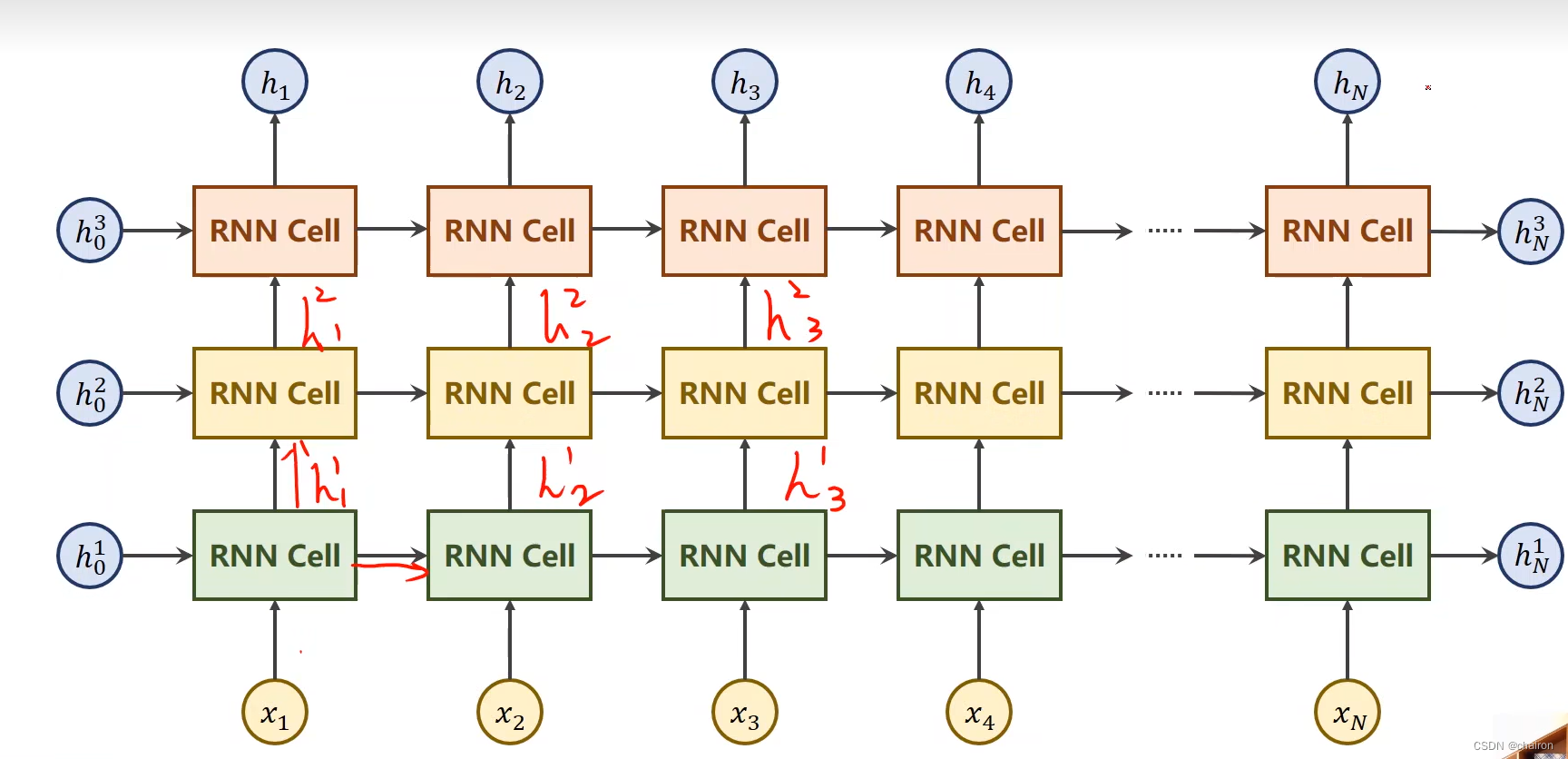
同一层的RNN Cell是同一个,以上其实只有3层。
# 练习2
import torch
batch_size=1
seq_len=3
input_size=4
hidden_size=2
num_layers=1
#Construction of RNN
cell=torch.nn.RNN(input_size,hidden_size,num_layers)
cell1=torch.nn.RNN(input_size,hidden_size,num_layers,batch_first=True)
#(seq,batch,inputSize)
inputs= torch.randn(seq_len,batch_size,input_size)
inputs1=torch.randn(batch_size,seq_len,input_size)
#初始化hidden为0
hidden =torch.zeros(num_layers,batch_size,hidden_size)
out,hidden=cell(inputs,hidden)
# out,hidden=cell1(inputs1,hidden)
print('Output size:',out.shape)#The shape of output is:[𝒔𝒆𝒒𝑺𝒊𝒛𝒆, 𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆, 𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛]
print('Output:',out)
print('Hidden size:',hidden.shape)#The shape of hidden is:[𝒏𝒖𝒎𝑳𝒂𝒚𝒆𝒓𝒔, 𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆, 𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛]
print("Hidden",hidden)
注意:
batch_first=True:输入数据的batch_size需要放在最前面。很多时候batch需要放在最前面。
结果:
Output size: torch.Size([3, 1, 2])
Output: tensor([[[ 0.7220, -0.1743]],
[[-0.2194, -0.1024]],
[[ 0.5668, -0.0651]]], grad_fn=<StackBackward0>)
Hidden size: torch.Size([1, 1, 2])
Hidden tensor([[[ 0.5668, -0.0651]]], grad_fn=<StackBackward0>)
RNN例子
训练一个模型将:“hello” ->“ohlol”(seq to seq)
使用RNN Cell实现
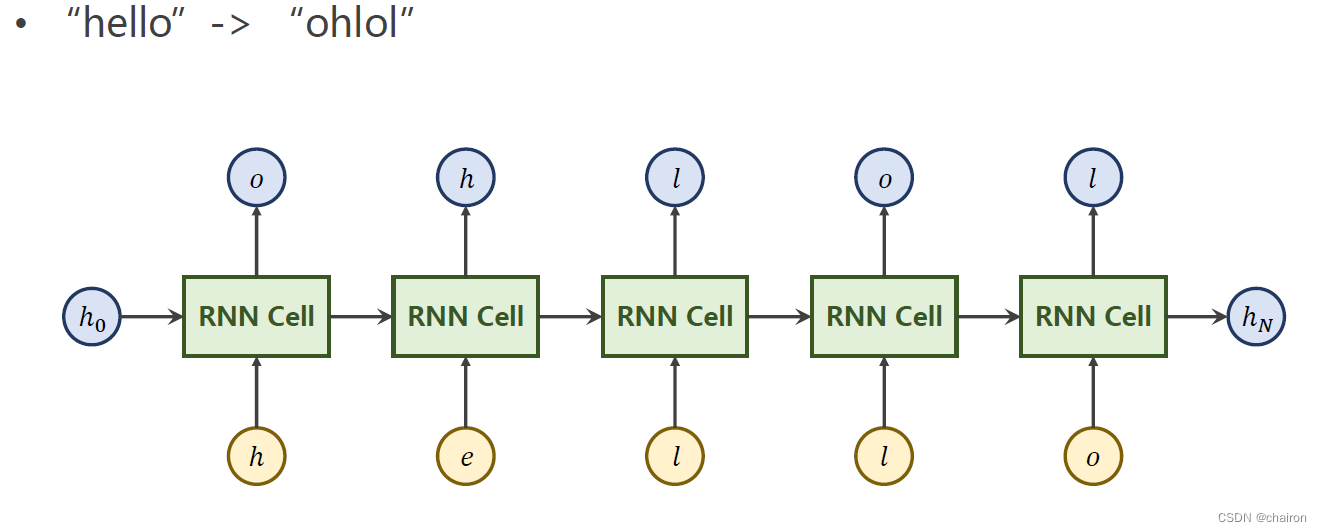
- RNNcell的输入应该是一组向量,我们需要将序列进行转换,转换为独热向量(One-Hot Vectors):
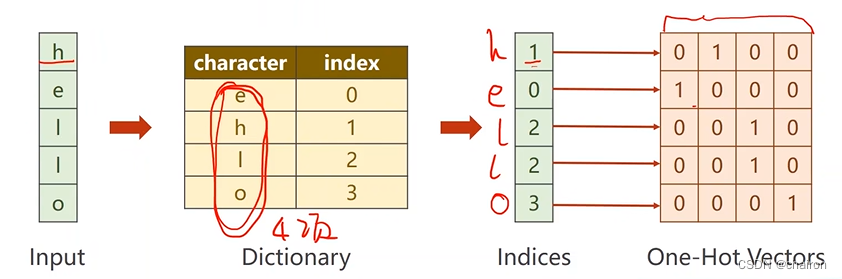
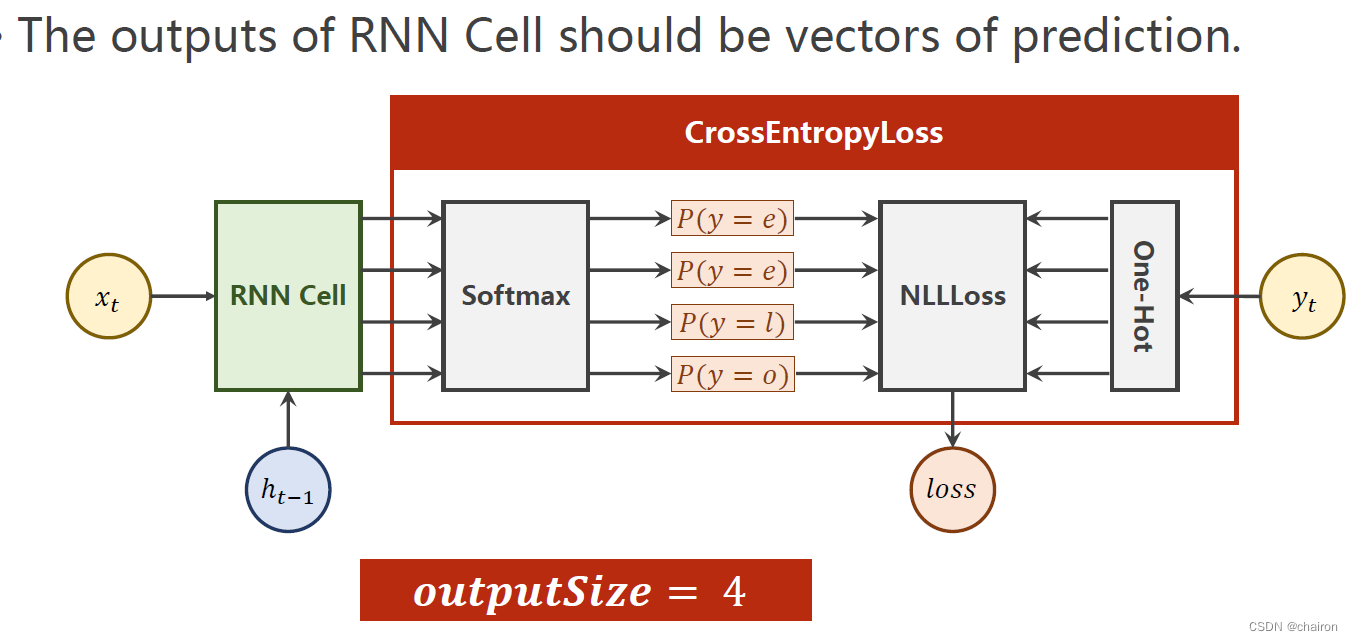
RNNCell结果通过softmax转化为多分类问题,然后计算交叉熵损失。
#练习3 use RNNCell
import torch
# parameters
hidden_size = 4
input_size = 4
batch_size = 1
idx2char = ['e', 'h', 'l', 'o']#字典
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]
one_hot_lookup=[[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]]
x_one_hot=[one_hot_lookup[x]for x in x_data]#将x的索引转换为独热向量
inputs=torch.Tensor(x_one_hot).view(-1,batch_size,input_size)#(𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
labels=torch.LongTensor(y_data).view(-1,1)#(𝒔𝒆𝒒𝑳𝒆𝒏,𝟏)
class Model(torch.nn.Module):
def __init__(self,input_size,hidden_size,batch_size):
super(Model, self).__init__()
#初始化参数
self.batch_size=batch_size
self.input_size=input_size
self.hidden_size=hidden_size
self.rnncell=torch.nn.RNNCell(input_size=input_size,#(𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
hidden_size=hidden_size)#(𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛𝒆)
def forward(self, input,hidden):
hidden=self.rnncell(input,hidden)
return hidden
def init_hidden(self):
return torch.zeros(self.batch_size,self.hidden_size)#初始化隐藏层
net=Model(input_size,hidden_size,batch_size)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.1)
#训练
for epoch in range(15):
loss=0
optimizer.zero_grad()#梯度清零
hidden=net.init_hidden()
print("Predicted string:",end='')
# input:(𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)->input:(𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
for input,label in zip(inputs,labels):
hidden=net(input,hidden)#RNNcell
loss+=criterion(hidden,label)
_,idx=hidden.max(dim=1)
print(idx2char[idx.item()],end='')
loss.backward()#backward
optimizer.step()#更新
print(', Epoch [%d/15] loss = %.3f' % (epoch + 1, loss.item()))
结果:
Predicted string:ooool, Epoch [1/15] loss = 5.873
Predicted string:ooool, Epoch [2/15] loss = 5.184
Predicted string:oooll, Epoch [3/15] loss = 5.083
Predicted string:oolll, Epoch [4/15] loss = 4.925
Predicted string:ollll, Epoch [5/15] loss = 4.669
Predicted string:ollll, Epoch [6/15] loss = 4.335
Predicted string:oooll, Epoch [7/15] loss = 4.070
Predicted string:oholl, Epoch [8/15] loss = 3.936
Predicted string:oholl, Epoch [9/15] loss = 3.841
Predicted string:oholl, Epoch [10/15] loss = 3.739
Predicted string:ohlll, Epoch [11/15] loss = 3.635
Predicted string:ohlll, Epoch [12/15] loss = 3.541
Predicted string:ohlll, Epoch [13/15] loss = 3.459
Predicted string:ohlll, Epoch [14/15] loss = 3.380
Predicted string:ohlll, Epoch [15/15] loss = 3.298
使用RNN实现
#练习4 use RNN
import torch
# parameters
input_size = 4
hidden_size = 4
num_layers = 1
batch_size = 1
seq_len = 5
idx2char = ['e', 'h', 'l', 'o']#字典
x_data = [1, 0, 2, 2, 3]
y_data = [3, 1, 2, 3, 2]
one_hot_lookup=[[1,0,0,0],
[0,1,0,0],
[0,0,1,0],
[0,0,0,1]]
x_one_hot=[one_hot_lookup[x]for x in x_data]#将x的索引转换为独热向量
inputs=torch.Tensor(x_one_hot).view(seq_len,batch_size,input_size)#(𝒔𝒆𝒒𝑳𝒆𝒏,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒊𝒏𝒑𝒖𝒕𝑺𝒊𝒛𝒆)
labels=torch.LongTensor(y_data)#(𝒔𝒆𝒒𝑳𝒆𝒏×𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝟏)变成二维矩阵,方便使用交叉熵损失计算
class Model(torch.nn.Module):
def __init__(self,input_size, hidden_size,batch_size,num_layers=1):
super(Model, self).__init__()
self.input_size=input_size
self.hidden_size=hidden_size
self.batch_size=batch_size
self.num_layers=num_layers
self.rnn = torch.nn.RNN(input_size=input_size,
hidden_size=hidden_size,
num_layers=num_layers)
def forward(self, input):
#hidden:(𝒏𝒖𝒎𝑳𝒂𝒚𝒆𝒓𝒔,𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛𝒆) 初始化隐层
hidden=torch.zeros(self.num_layers,
self.batch_size,
self.hidden_size)
out,_=self.rnn(input,hidden)
return out.view(-1,self.hidden_size)
#reshape:(𝒔𝒆𝒒𝑳𝒆𝒏×𝒃𝒂𝒕𝒄𝒉𝑺𝒊𝒛𝒆,𝒉𝒊𝒅𝒅𝒆𝒏𝑺𝒊𝒛𝒆):变成二维矩阵,方便使用交叉熵损失计算
net = Model(input_size,hidden_size,batch_size,num_layers)
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)
for epoch in range(15):
#Training step
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# _,idx = outputs.max(dim=1)
# idx = idx.data.numpy()
idx = outputs.argmax(dim=1)
idx=idx.data.numpy()
print('Predicted: ', ''.join([idx2char[x] for x in idx]), end='')
print(', Epoch [%d/15] loss = %.3f' % (epoch + 1, loss.item()))
结果:
Predicted: eeeee, Epoch [1/15] loss = 1.440
Predicted: oelll, Epoch [2/15] loss = 1.304
Predicted: oelll, Epoch [3/15] loss = 1.183
Predicted: ohlll, Epoch [4/15] loss = 1.084
Predicted: ohlll, Epoch [5/15] loss = 1.002
Predicted: ohlll, Epoch [6/15] loss = 0.932
Predicted: ohlll, Epoch [7/15] loss = 0.865
Predicted: ohlol, Epoch [8/15] loss = 0.800
Predicted: ohlol, Epoch [9/15] loss = 0.740
Predicted: ohlol, Epoch [10/15] loss = 0.693
Predicted: ohlol, Epoch [11/15] loss = 0.662
Predicted: ohlol, Epoch [12/15] loss = 0.641
Predicted: ohlol, Epoch [13/15] loss = 0.625
Predicted: ohlol, Epoch [14/15] loss = 0.611
Predicted: ohlol, Epoch [15/15] loss = 0.599
嵌入层 Embedding
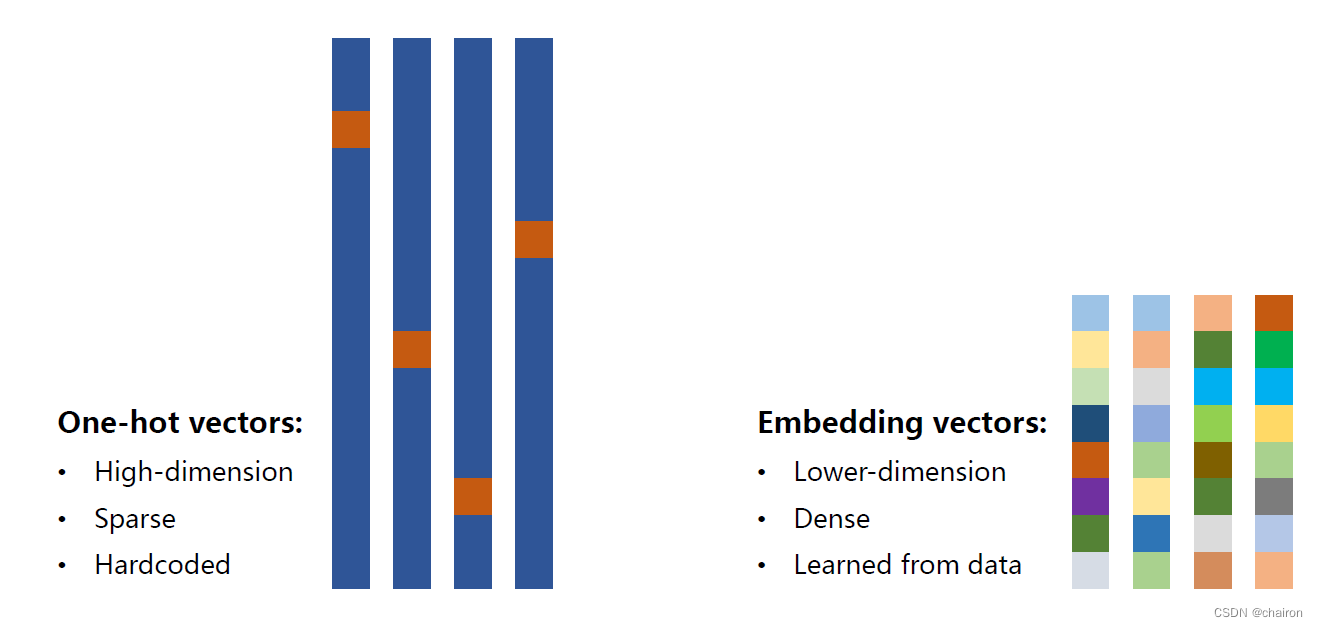
独热向量的缺点
- 维度太高(维度爆炸)
- 稀疏
- 硬编码(每个词对应每个向量,不是学习出来的)
那么能不能找到一个变换,把词的编码变成:
- 低纬
- 稠密
- 从数据中学习
Embedding
将高维的、稀疏向量映射到低纬稠密的空间里。(也就是降维)
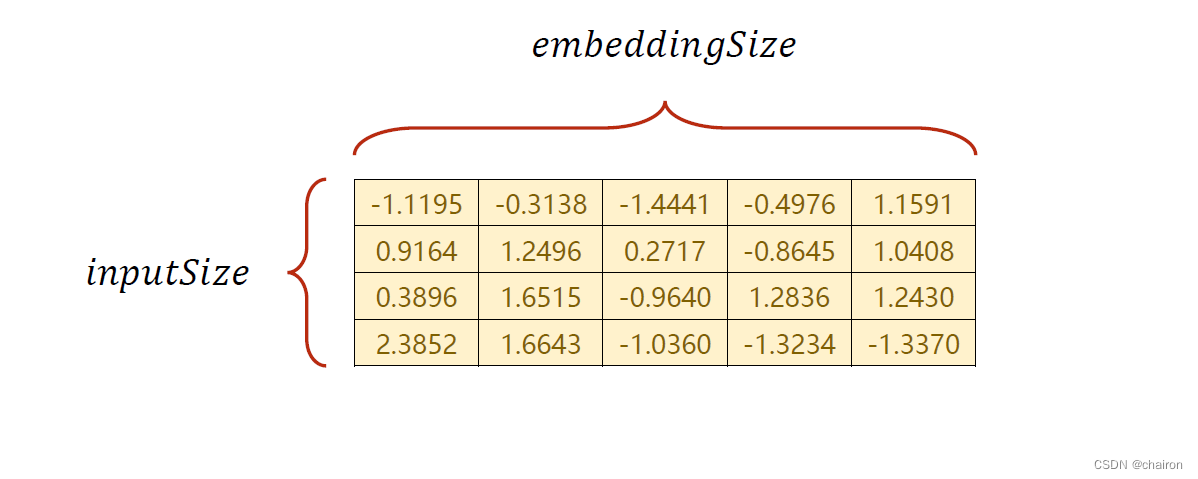
假设输入是4维的,嵌入层是5维,则需要构造如下的矩阵:
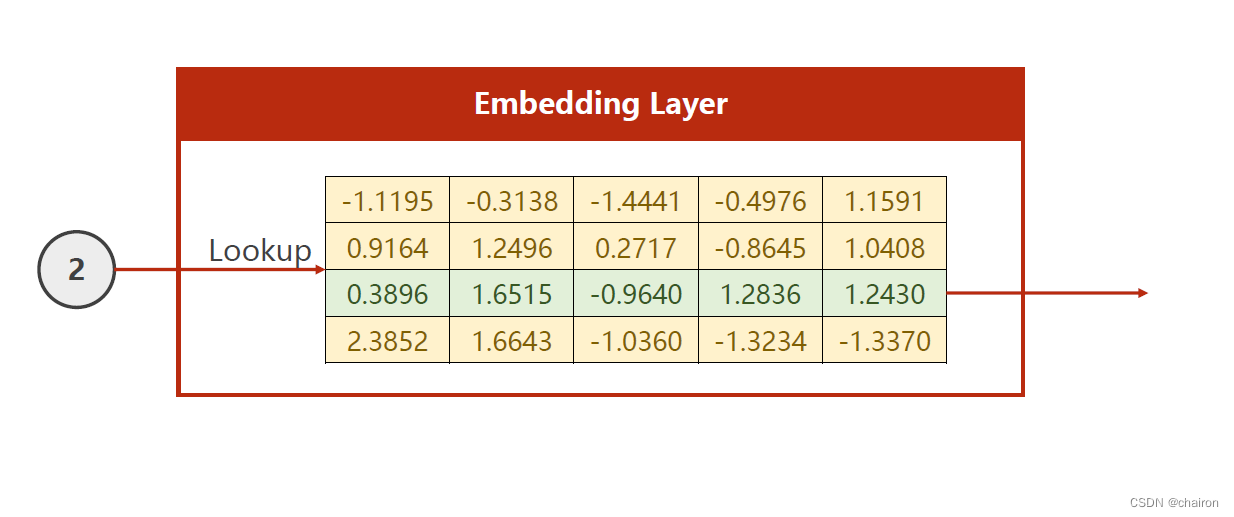
假设要查找的是2:从矩阵中输出对应那一行数据
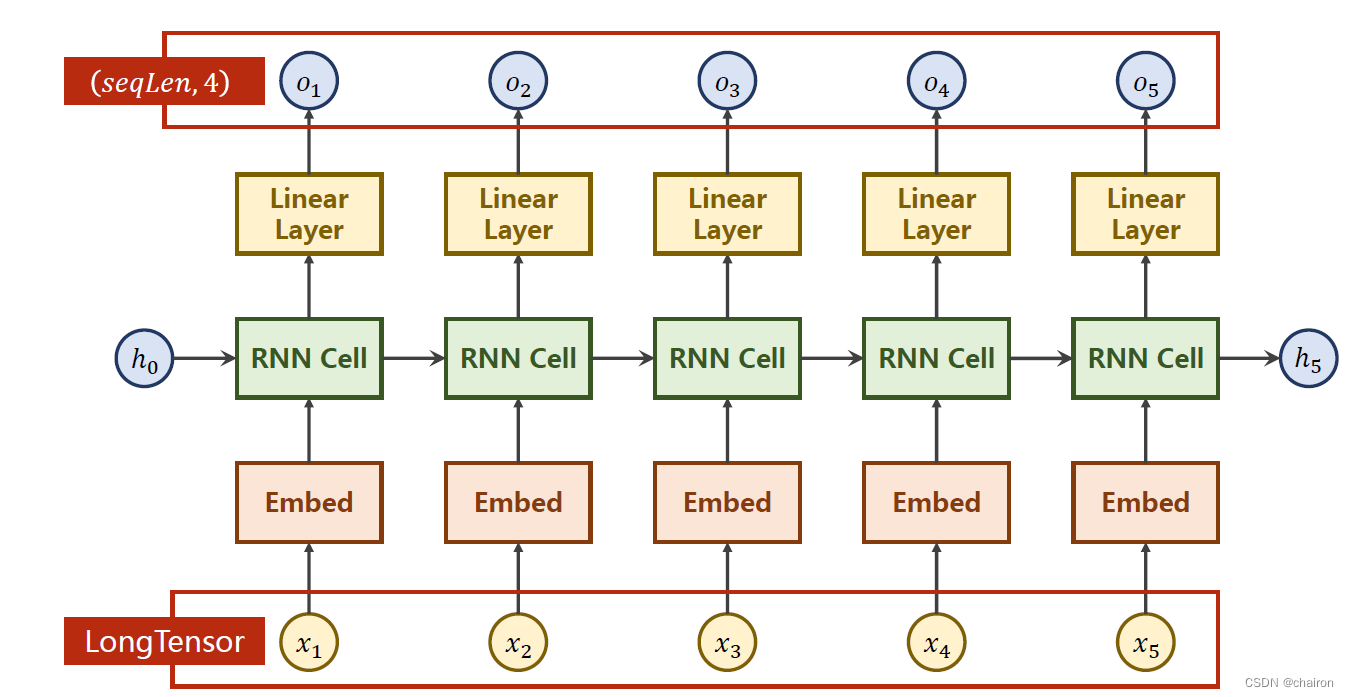
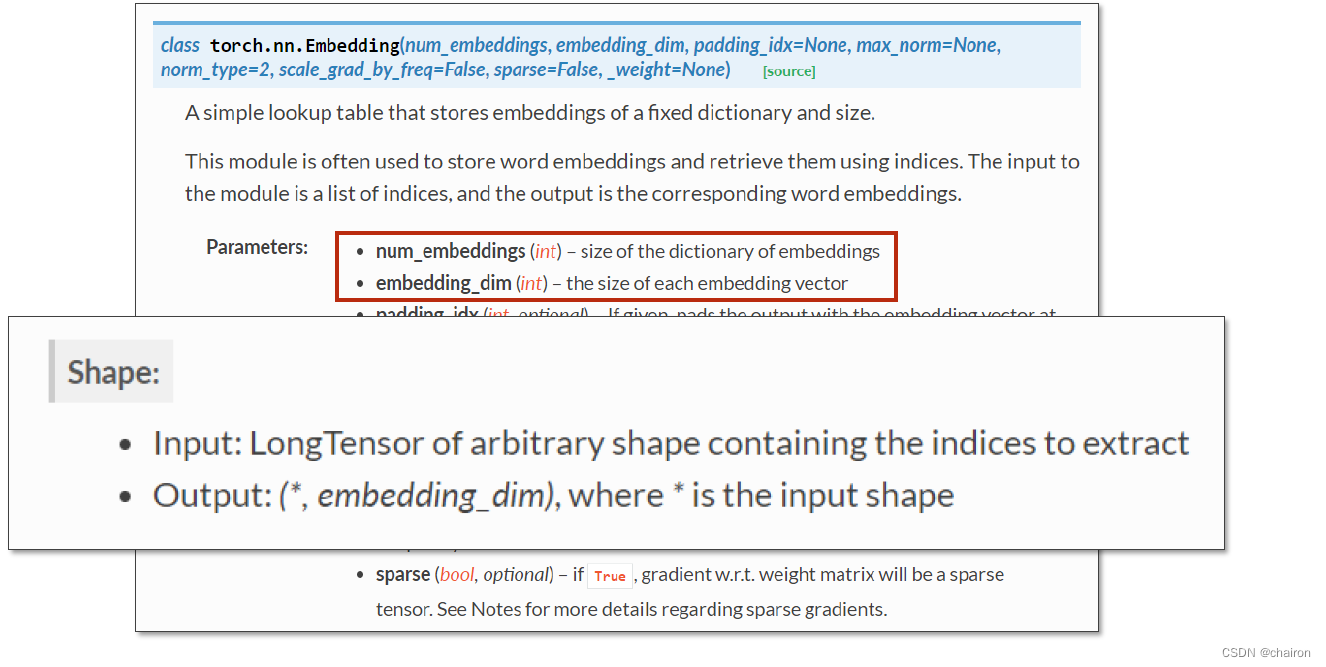
- torch.nn.Embedding:
- num_embeddings:embbeding size,嵌入层的维度()
- embedding_dim:每一个输入数据的向量维度(比如说,x1~x5都是4维)


#练习5 Use Embedding
import torch
# parameters
num_class = 4
input_size = 4
hidden_size = 8
embedding_size = 10
num_layers = 2
batch_size = 1
seq_len = 5
idx2char = ['e', 'h', 'l', 'o']
x_data = [[1, 0, 2, 2, 3]]# (batch, seq_len)
y_data = [3, 1, 2, 3, 2] # (batch * seq_len)
inputs = torch.LongTensor(x_data)
labels = torch.LongTensor(y_data)
class Model(torch.nn.Module):
def __init__(self):
super(Model, self).__init__()
self.emb = torch.nn.Embedding(input_size, embedding_size)
self.rnn = torch.nn.RNN(input_size=embedding_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True)
self.fc = torch.nn.Linear(hidden_size, num_class)
def forward(self, x):
# hidden = (torch.zeros(num_layers, x.size(0), hidden_size),torch.zeros(num_layers, x.size(0), hidden_size))#The LSTM requires two hidden states
hidden=torch.zeros(num_layers, x.size(0), hidden_size)
x= self.emb(x) # (batch, seqLen, embeddingSize)
x,states= self.rnn(x, hidden)#返回类型为tuble,切割tubel by splitting up the tuple so that out is just your output tensor.
#out then stores the hidden states, while states is another tuple that contains the last hidden and cell state.
x = self.fc(x)
return x.view(-1, num_class)
net = Model()
criterion = torch.nn.CrossEntropyLoss()
optimizer = torch.optim.Adam(net.parameters(), lr=0.05)
for epoch in range(15):
optimizer.zero_grad()
outputs = net(inputs)
loss = criterion(outputs, labels)
loss.backward()
optimizer.step()
# _,idx = outputs.max(dim=1)
# idx = idx.data.numpy()
idx = outputs.argmax(dim=1)
idx=idx.data.numpy()
print('Predicted: ', ''.join([idx2char[x] for x in idx]), end='')
print(', Epoch [%d/15] loss = %.3f' % (epoch + 1, loss.item()))
结果:
Predicted: ooooo, Epoch [1/15] loss = 1.441
Predicted: ooooo, Epoch [2/15] loss = 1.148
Predicted: ooool, Epoch [3/15] loss = 1.007
Predicted: olool, Epoch [4/15] loss = 0.884
Predicted: olool, Epoch [5/15] loss = 0.760
Predicted: ohool, Epoch [6/15] loss = 0.609
Predicted: ohlol, Epoch [7/15] loss = 0.447
Predicted: ohlol, Epoch [8/15] loss = 0.313
Predicted: ohlol, Epoch [9/15] loss = 0.205
Predicted: ohlol, Epoch [10/15] loss = 0.135
Predicted: ohlol, Epoch [11/15] loss = 0.093
Predicted: ohlol, Epoch [12/15] loss = 0.066
Predicted: ohlol, Epoch [13/15] loss = 0.047
Predicted: ohlol, Epoch [14/15] loss = 0.033
Predicted: ohlol, Epoch [15/15] loss = 0.024
LSTM
- 现在常用的memory管理方式叫做长短期记忆(Long Short-term Memory),简称LSTM
- LSTM对信息进行选择性的保留,是通过门控机制进行实现的。(即可以选择保留觉得有用的信息,遗忘觉得没用的信息。)
- 冷知识:可以被理解为比较长的短期记忆,因此是short-term,而非是long-short term
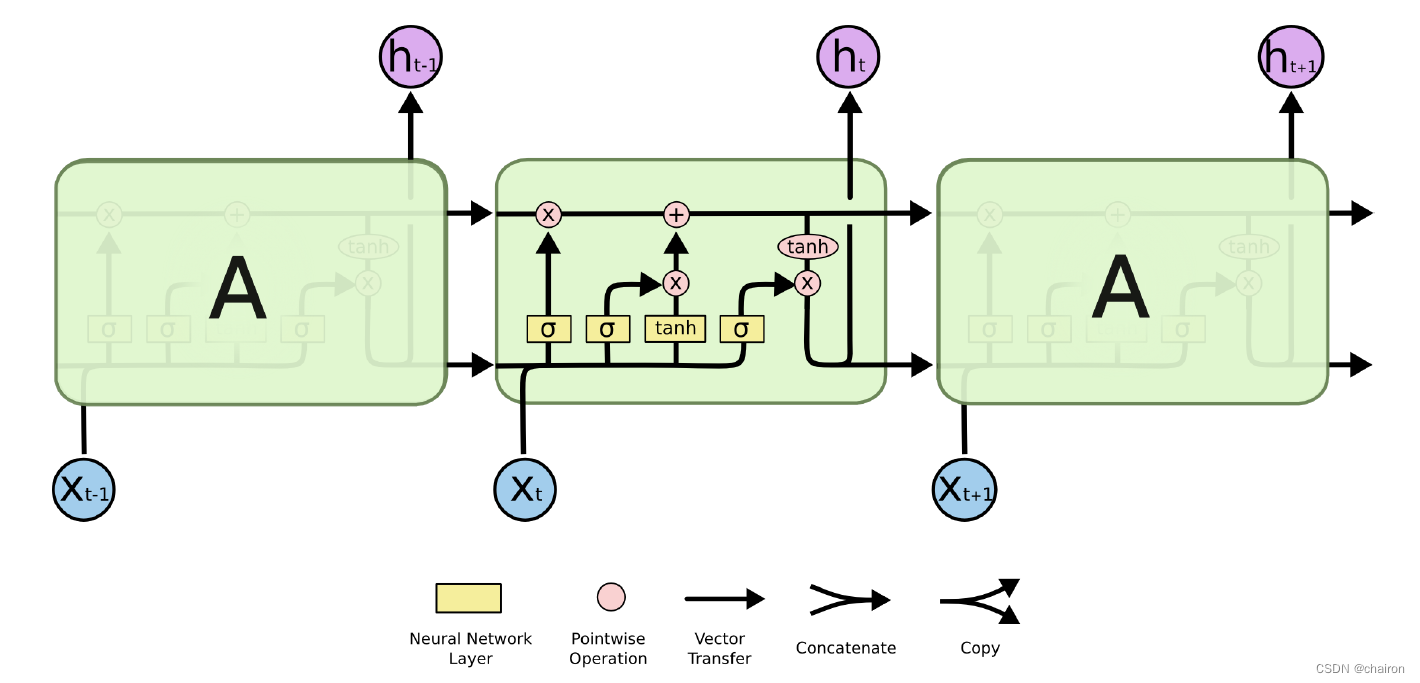

官网文档
self.rnn=torch.nn.LSTM(input_size=embedding_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True)
LSMT学习能力比RNN强,但是时间复杂度高,训练时间长!
GRU(门控循环单元)
GRU 旨在解决标准 RNN 中出现的梯度消失问题。GRU 也可以被视为 LSTM 的变体,因为它们基础的理念都是相似的,且在某些情况能产生同样出色的结果。
GRU 背后的原理与 LSTM 非常相似,即用门控机制控制输入、记忆等信息而在当前时间步做出预测:
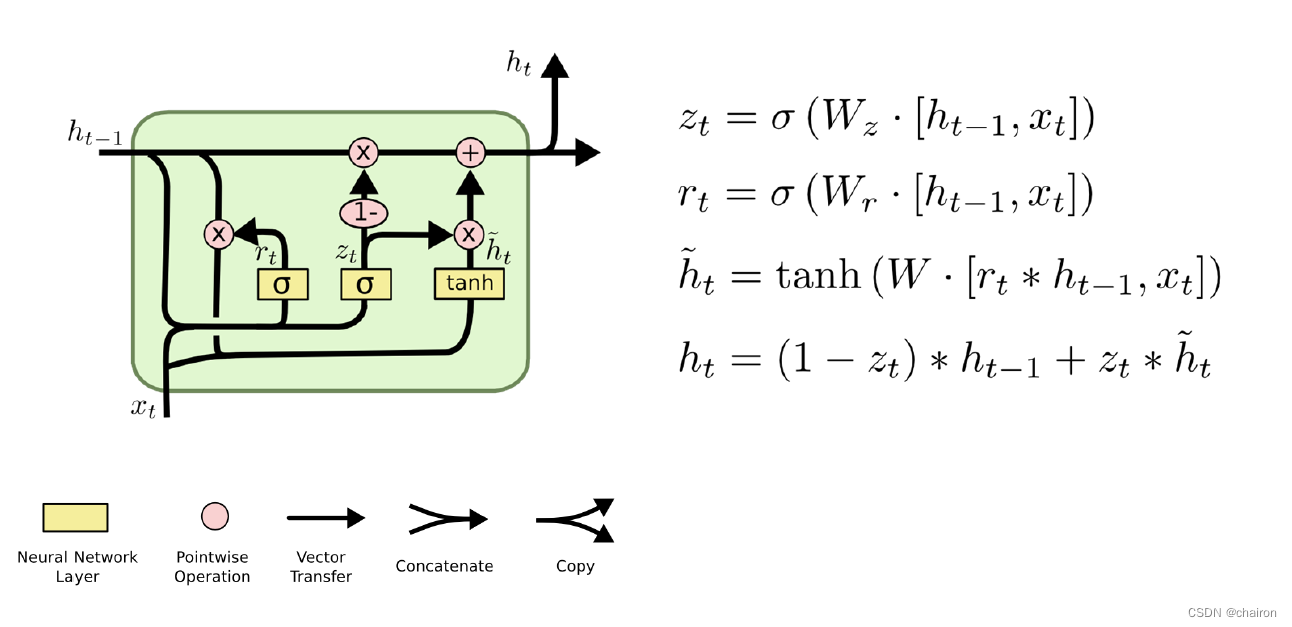
self.rnn=torch.nn.GRAU(input_size=embedding_size,
hidden_size=hidden_size,
num_layers=num_layers,
batch_first=True)
练习
请用LSTM 和GRU完成训练。
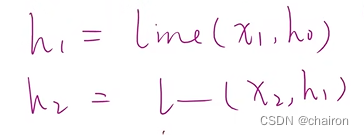








![绝地求生:[更新周报] 3/20 不停机更新:商城无上新、23号七周年HOT TIME!](https://img-blog.csdnimg.cn/direct/bdf5c3af28954ff5be15dfd350e68e68.png)