从标题来看这堂课跟评估指标有关,而且是专门针对分类器的评估指标

如下图,解释了 “为什么 metrics 很重要”
1.训练目标 (成本函数) 仅仅是现实世界目标的一个代理 (proxy)
2.理想的训练目标应该是指标 metric,但这并不总是可能的。metrics 指标对于模型评估来说是有用且重要的
3.指标会帮助我们把一个商业目标转化为一个量化的目标
4.指标会帮助 ML开发团队 向目标前进 (通过提高模型在指标上的性能,来向目标前进)
5.用来量化下面这些东西的 “gap” 比较有用:
- 目标性能和基线
- 目标性能和当前性能
- 随着时间测量进度
6.用于调试和诊断 “偏差 vs 方差”

如下图是二元分类器的相关总结
二元分类器有两种模型:
1.输出一个范畴类(比如决策树)
2.输出一个实数值分数(比如 SVM, 逻辑回归、神经网络)

TODO: 什么是 HM? 什么是 GM?
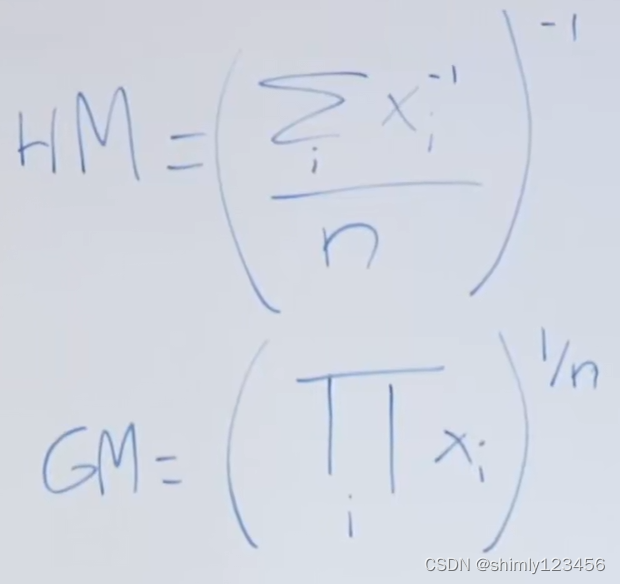


![[uni-app] uni.createAnimation动画在APP端无效问题记录](https://img-blog.csdnimg.cn/direct/08ec8d91dd4e4142a75226e74bacc547.png)