参考及转载内容：

• 循环神经网络（RNN）
• 深度学习05-RNN循环神经网络
• 完全理解RNN（循环神经网络）

传统的CNN（Covolutional Neural Network，卷积神经网络）通常是给定输入预测对应的输出，是一对一的关系（输入层->隐藏层->输出层，隐藏层之间无关联，为顺序传播的关系），没有涉及输入信息间的关联关系。而在实际应用中，如自然语言处理、语音处理、时序数据处理等任务都依赖于上下文的输入才能够确定输出，因此CNN就无法很好地解决此类任务所需的关联关系提取。

RNN（Recurrent Neural Network，循环神经网络）就是针对这一类需要考虑上下文信息的数据分析与处理提出来的网络架构，循环神经网络的隐藏层会对之前的信息进行记忆存储，隐藏层之间的信息可以进行交互，当前隐藏层的输入可以包含上一个隐藏层的输出、上一个隐藏层存储的信息状态、输入层的输出。

经典RNN

单向RNN

假设$x_t$表示第$t$步的输入，$s_t$表示第$t$步的隐藏层的状态，该状态是根据上一个隐藏层状态$s_{t-1}$计算得出，假设$U$表示输入层的链接矩阵，$W$表示上一个隐藏时刻到下一个隐藏时刻的权重矩阵，$f(x)$为非线性层的激活函数，一般为$tanh$或$ReLU$，则时刻$t$的隐藏层计算为：$$s_t=f(U{x}_t+W{s}_{t-1})$$则时刻t的输出计算为：$$o_t=g(V\ast s_t)$$其中$V$表示输出层的权重矩阵，$g(x)$为激活函数。可以看到当前时刻的输出与多个历史时刻的数据相关，因为每个当前时刻的输出都受到上个时刻的影响。但是单向RNN仅考虑了历史信息，很多时候需要共同结合上下文信息才能够得到更好的预测结果。

# pytorch中的单向RNN
import torch
import torch.nn as nn

# 定义输入数据
input_size = 10   # 输入特征的维度
sequence_length = 5   # 时间步个数
batch_size = 3   # 批次大小

# 创建随机输入数据
#输入数据的维度为(sequence_length, batch_size, input_size)，表示有sequence_length个时间步，
#每个时间步有batch_size个样本，每个样本的特征维度为input_size。
input_data = torch.randn(sequence_length, batch_size, input_size)
print("输入数据",input_data)
# 定义RNN模型
# 定义RNN模型时，我们指定了输入特征的维度input_size、隐藏层的维度hidden_size、隐藏层的层数num_layers等参数。
# batch_first=False表示输入数据的维度中批次大小是否在第一个维度，我们在第二个维度上。
rnn = nn.RNN(input_size, hidden_size=20, num_layers=1, batch_first=False)
"""
在前向传播过程中，我们将输入数据传递给RNN模型，并得到输出张量output和最后一个时间步的隐藏状态hidden。
输出张量的大小为(sequence_length, batch_size, hidden_size)，表示每个时间步的隐藏层输出。
最后一个时间步的隐藏状态的大小为(num_layers, batch_size, hidden_size)。
"""
# 前向传播，第二个参数h0未传递，默认为0
output, hidden = rnn(input_data)
print("最后一个隐藏层",hidden.shape)
print("输出所有隐藏层",output.shape)

# 打印每个隐藏层的权重和偏置项
# weight_ih表示输入到隐藏层的权重，weight_hh表示隐藏层到隐藏层的权重，注意这里使出是转置的结果。
# bias_ih表示输入到隐藏层的偏置，bias_hh表示隐藏层到隐藏层的偏置。
for name, param in rnn.named_parameters():
    if 'weight' in name or 'bias' in name:
        print(name, param.data)

单向RNN的参数是共享的，RNN参数共享指的是：在每一个时间步上，所对应的参数是共享的。参数共享的目的有两个：一、用这些参数来捕获序列上的特征；二、共享参数减少模型的复杂度。

对于RNN的参数共享，我们可以理解为对于一个句子或者文本，参数U可以看成是语法结构、参数W是一般规律，而下一个单词的预测必须是上一个单词和一般规律W与语法结构U共同作用的结果。我们知道，语法结构和一般规律在语言当中是共享的。所以，参数自然就是共享的！

我们需要记住的是，深度学习是怎么减少参数的，很大原因就是参数共享，而CNN是在空间上共享参数，RNN是在时间序列上共享参数。

双向RNN

这种可以结合上下文信息的RNN结构即双向RNN，双向RNN的隐藏层需要保存两个状态值，一个是正向计算，一个是反向计算，基于上述单向计算的过程，双向计算可表示如下：$$o_t=g(V\ast s_t+V^{\prime }\ast s_t^{\prime })$$
正向计算：$$s_t=f(U{x}_t+W{s}_{t-1})$$
反向计算：$$s_t^{\prime }=f(U^{\prime }{x}_t+W{s}_{t+1})$$
在正向计算和反向计算过程中，权重不共享。其中网络参数的更新是通过前向传播和反向传播过程完成的，其中反向传播的过程采用的是BPTT（BackPropagation Through Time）算法进行的，其实基本原理也是基于常规的BP算法，只是BPTT需要考虑不同时刻的梯度计算结果之和，具体计算可参考：BPTT算法推导 。

# pytorch定义双向RNN
import torch
import torch.nn as nn

# 定义输入数据
input_size = 10   # 输入特征的维度
sequence_length = 5   # 时间步个数
batch_size = 3   # 批次大小

# 创建随机输入数据
input_data = torch.randn(sequence_length, batch_size, input_size)

# 定义双向RNN模型
rnn = nn.RNN(input_size, hidden_size=20, num_layers=1, batch_first=False, bidirectional=True)

# 前向传播
output, hidden = rnn(input_data)

# 输出结果
print("输出张量大小：", output.size())
print("最后一个时间步的隐藏状态大小：", hidden.size())

Deep RNN

基本循环神经网络和双向循环神经网络只有单个隐藏层，有时不能很好的学习数据内部关系，可以通过叠加多个隐藏层，形成深度循环神经网络结构。单层的隐藏层RNN的参数是共享的，深层的RNN会有$L$层的参数，其每一层都可以是一个双向RNN结构。

# pytorch实现双向RNN
import torch
import torch.nn as nn

# 定义输入数据和参数
input_size = 5
hidden_size = 10
num_layers = 2
batch_size = 3
sequence_length = 4

# 创建输入张量
input_tensor = torch.randn(sequence_length, batch_size, input_size)

# 创建多层RNN模型
rnn = nn.RNN(input_size, hidden_size, num_layers)

# 前向传播
output, hidden = rnn(input_tensor)

# 打印输出张量和隐藏状态的大小
print("Output shape:", output.shape)
print("Hidden state shape:", hidden.shape)

RNN特性总结

• 单向单隐藏层传播参数共享；

• 参数更新采用BPTT的算法实现；
  

• 存在梯度消失和梯度爆炸的问题；

  • 梯度消失：传统的RNN不能捕获长距离词之间的关系。从图中可以看到tanh函数在x趋近于无穷大和无穷小时梯度值都为0，当邻近神经元梯度接近0时，因为前面层的梯度是由后面层的梯度连乘得到的，多个梯度相乘会使梯度值以指数级速度下降，最终在反向传播几步后就完全消失，比较远的时刻的梯度值为0。
  • 梯度爆炸：RNN的学习依赖于我们的激活函数和网络初始参数，如果Jacobian矩阵中的值太大，会产生梯度爆炸而不是梯度消失问题。梯度消失比梯度爆炸受到了更多的关注有两方面的原因。其一，梯度爆炸容易发现，梯度值会变成NaN，导致程序崩溃。其二，用预定义的阈值裁剪梯度可以简单有效的解决梯度爆炸问题。梯度消失问题就不容易发现并且也不好处理，这也是梯度消失比梯度爆炸受到学术界更多关注的原因。

• RNN的几种架构：

  • 单输入单输出（Single Input Single Output，SISO）： 给定一段文本，预测下一个词语；
    
    

  • 单输入多输出（Single Input Multiple Output，SIMO）：如上图有两种实现形式。这种1 to N的结构可以处理的问题有很多，比如图像标注，输入的X是图像的特征，而输出的y序列是一段句子。

  • 多输入单输出（Multiple Input Single Output，MISO）：输入是一个序列，输出是一个单独的值而不是序列。这种结构通常用来处理序列分类问题。如输入一段文字判别它所属的类别，输入一个句子判断其情感倾向，输入一段文档并判断它的类别等等。

  • 多输入多输出（Multiple Input Multiple Output，MIMO）：一种是NtoN，输入和输出序列是等长的。这种可以作为简单的Char RNN可以用来生成文章，诗歌，甚至是代码，非常有意思。另一种是这种结构又叫Encoder-Decoder模型，也称之为Seq2Seq模型。在现实问题中，我们遇到的大部分序列都是不等长的。如机器翻译中，源语言和目标语言的句子往往并没有相同的长度。而Encoder-Decoder结构先将输入数据编码成一个上下文向量c，之后在通过这个上下文向量输出预测序列。

变体RNN

参考链接：【译】理解LSTM（通俗易懂版）

LSTM

RNN的结构的隐藏层只有一个状态，对邻近的输入会非常敏感，如果我们再增加一个门（gate）来控制特征的流通和损失，即c，让它来保存长期的状态，这就是长短时记忆网络(Long Short Term Memory，LSTM)。

新增加的状态c，称为单元状态。我们把LSTM按照时间维度展开：
其中图像上的标识$\sigma$标识使用sigmod激活到[0-1],tanh激活到[-1,1]，⨀ 是一个数学符号，表示逐元素乘积（element-wise product）或哈达玛积（Hadamard product）。当两个相同维度的矩阵、向量或张量进行逐元素相乘时，可以使用 ⨀ 符号来表示。

LSTM的输入有三个：当前时刻网络的输出值$x_t$、上一时刻LSTM的输出值$h_{t-1}$ 、以及上一时刻的记忆单元向量$c_{t-1}$；

LSTM的输出有两个：当前时刻LSTM输出值$h_t$、当前时刻的隐藏状态向量$h_t$、和当前时刻的记忆单元状态向量$c_t$。

注意：记忆单元c在LSTM 层内部结束工作，不向其他层输出。LSTM的输出仅有隐藏状态向量h。

LSTM 的关键是单元状态，即贯穿图表顶部的水平线，有点像传送带。这一部分一般叫做单元状态（cell state）它自始至终存在于LSTM的整个链式系统中。

$f_t$叫做遗忘门，表示$C_{t-1}$ 的哪些特征被用于计算$C_t$，$f_t$是一个向量，向量的每个元素均位于(0~1)范围内。通常我们使用 sigmoid 作为激活函数，sigmoid 的输出是一个介于于(0~1)区间内的值，但是当你观察一个训练好的LSTM时，你会发现门的值绝大多数都非常接近0或者1，其余的值少之又少。

$C_t$表示单元状态更新值，由输入数据$x_t$和隐节点$h_{t-1}$经由一个神经网络层得到，单元状态更新值的激活函数通常使用tanh。 $i_t$叫做输入门，同 $f_t$一样也是一个元素介于(0~1)区间内的向量，同样由$x_t$和$h_{t-1}$经由sigmoid激活函数计算而成。

最后，为了计算预测值$y^t$和生成下个时间片完整的输入，我们需要计算隐节点的输出$h_t$

GRU

Gated Recurrent Unit – GRU 是 LSTM 的一个变体。他保留了 LSTM 划重点，遗忘不重要信息的特点，在long-term 传播的时候也不会被丢失。

LSTM 的参数太多，计算需要很长时间。因此，最近业界又提出了 GRU（Gated RecurrentUnit，门控循环单元）。GRU 保留了 LSTM使用门的理念，但是减少了参数，缩短了计算时间。

相对于 LSTM 使用隐藏状态和记忆单元两条线，GRU只使用隐藏状态。异同点如下：

GRU的计算过程如下：

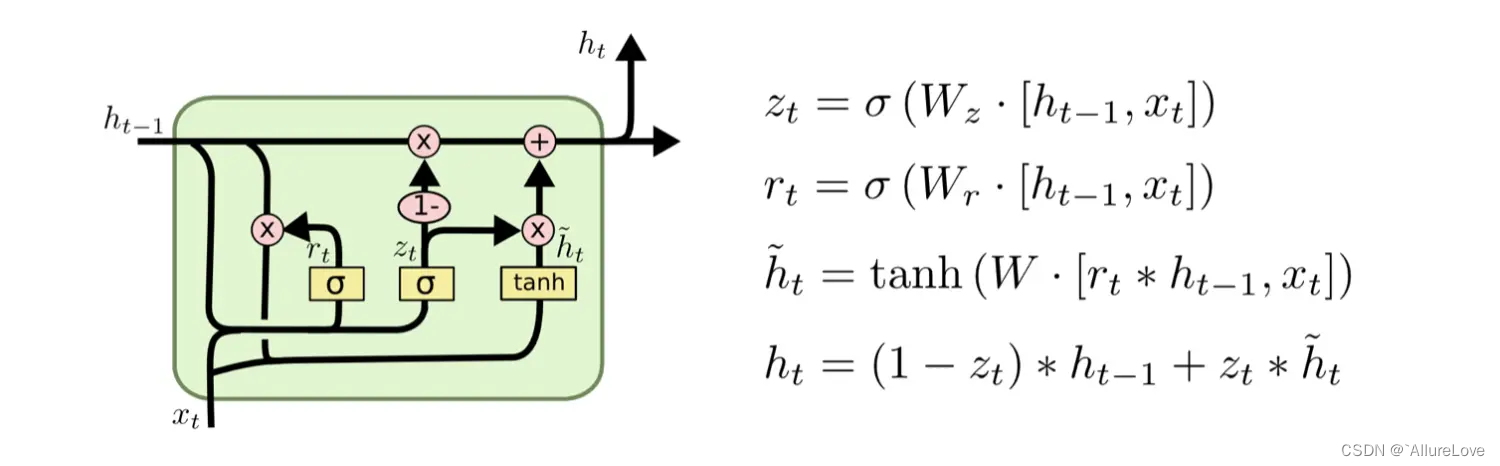
如图所示，GRU 没有记忆单元，只有一个隐藏状态h在时间方向上传播。这里使用r和z共两个门（LSTM 使用 3 个门），r称为 reset 门，z称为 update 门。r（reset门）决定在多大程度上“忽略”过去的隐藏状态，定义了前面记忆保存到当前时间步的量。