相关峭度解卷积MCKD是一种新的解卷积方法，其设计了一个新的目标函数—相关峭度，并以此为优化目标设计一系列的FIR滤波器，为实现最好的效果，需要从中找到最优滤波器并最终实现对信号中噪声的抑制和对信号中冲击成分的突出的目的。MCKD能够以重现轴承信号中的周期特性为目标，最大限度地突出含噪信号中的冲击成分，这对于轴承早期故障的故障诊断来说具有重要意义。比如可以将CEEMD和MCKD相结合，即可以解决CEEMD分解后无法提取出淹没在背景噪声中微弱信号特征的问题，又保持了信号的完备性，避免了有用信息的损失。

MCKD算法充分考虑了振动信号中所蕴含的周期性瞬态冲击特性，通过迭代方式以解卷积信号相关峭度最大化为目标来设计逆滤波器，恢复信号中被强烈噪声所掩盖的连续性脉冲。

MCKD算法中涉及的主要参数有滤波器长度L、解卷积周期T、移位数M。滤波器长度L决定了滤波器的分辨率，影响着滤波器的结构和滤波效果。解卷积周期T指的是振动信号中相邻两个冲击序列之间的数据点数，由轴承的结构参数、实际转速和采样频率共同决定，解卷积周期的准确性对故障诊断效果有着至关重要的影响，对故障冲击信号周期估计误差越大，解卷积效果越差。移位数M影响着振动信号解卷积后突出的冲击脉冲个数。MCKD算法本质上是以解卷积信号相关峭度最大为目标设计FIR滤波器。由于滤波器的设计受滤波器长度L的影响，相关峭度的计算需要预先确定解卷积周期T和和移位数M。因此，L、T、M的取值将影响MCKD算法的故障特征提取效果。

鉴于此，提出一种改进的MCKD算法，该算法利用迭代算法估计信号周期，以解决盲解卷积方法中的先验周期问题，可迁移至金融时间序列，地震信号，机械振动信号，语音信号，声信号等一维时间序列信号，出图如下：

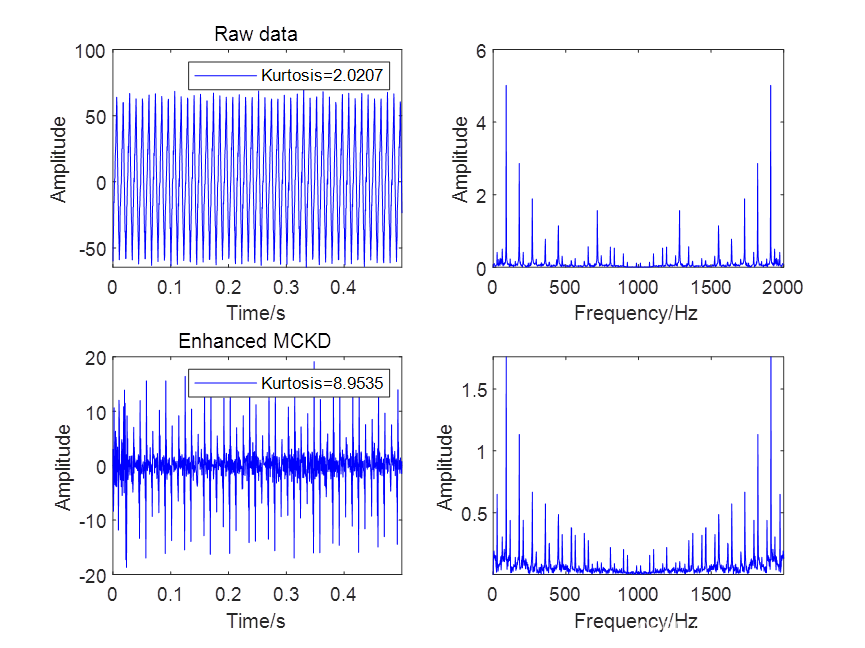
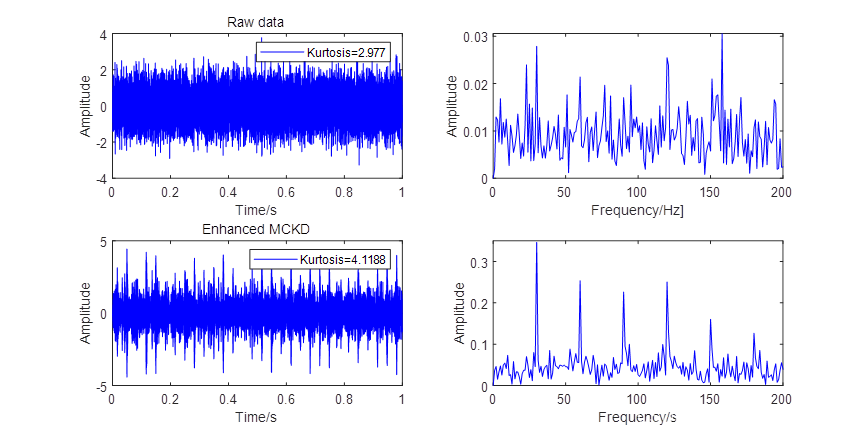
代码可通过知乎学术咨询获得：MATLAB环境下基于改进最大相关峭度解卷积的滚动轴承故障诊断

https://www.e/792359672131756032工学博士，担任《Mechanical System and Signal Processing》审稿专家，担任《中国电机工程学报》优秀审稿专家，《控制与决策》，《系统工程与电子技术》，《电力系统保护与控制》，《宇航学报》等EI期刊审稿专家。

擅长领域：现代信号处理，机器学习，深度学习，数字孪生，时间序列分析，设备缺陷检测、设备异常检测、设备智能故障诊断与健康管理PHM等。