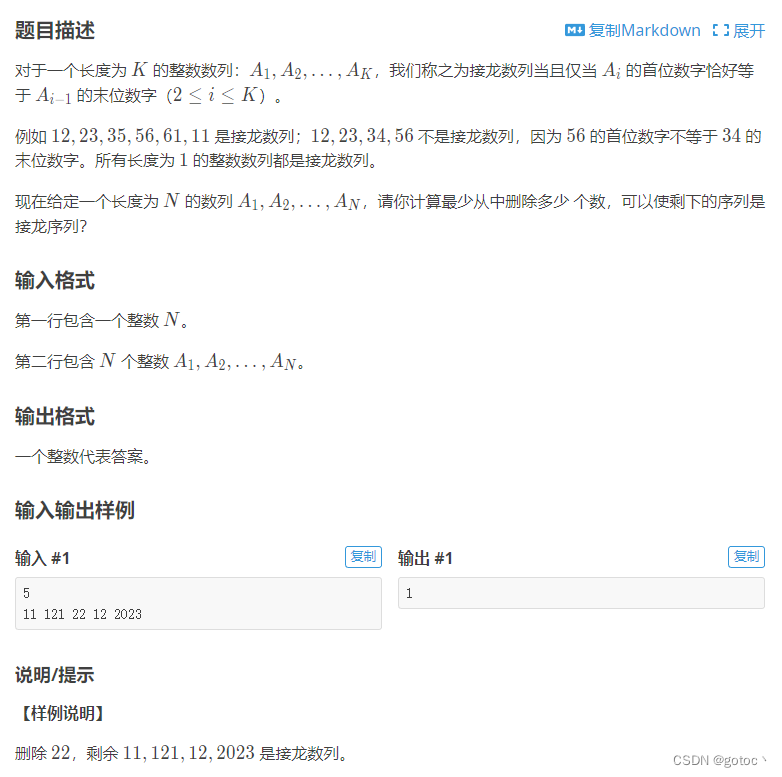
【题目描述】

利用公式

求一元二次方程ax²+bx+c=0的根，其中a不等于0。结果要求精确到小数点后5位。

【输入】

输入一行，包含三个浮点数a,b,c（它们之间以一个空格分开），分别表示方程ax²+bx+c=0的系数。

【输出】

输出一行，表示方程的解。

若两个实根相等，则输出形式为：“x1=x2=...”；

若两个实根不等，在满足根小者在前的原则，则输出形式为：“x1=...;x2=...“；

若无实根输出“No answer!”。

所有输出部分要求精确到小数点后5位，数字、符号之间没有空格。

【输入样例】

-15.97 19.69 12.02

【输出样例】

x1=-0.44781;x2=1.68075

【参考答案】：

#include<bits/stdc++.h>
using namespace std;
double a,b,c,x1,x2,s,x;
int main(){
	cin>>a>>b>>c;
	x1=(-b+sqrt(b*4-4*a*c))/(2*a);
	x2=(-b-sqrt(b*b-4*a*c))/(2*a);
	s=-b/(2*a);
	if(-b==0) s=0;
	x=sqrt(4*a*c-b*b)/(2*a);
	if(b*b==4*a*c) printf("x1=x2=%.5f",x1);
	if(b*b>4*a*c) printf("x1=%.5f;x2==%.5f",x1,x2);
	if(b*b<4*a*c) printf("x1=%.5f+%.5fi;x2=%.5f-%.5fi",s,x,s,x);
	
	return 0;
}