[蓝桥杯 2023 省 A] 更小的数
题目描述
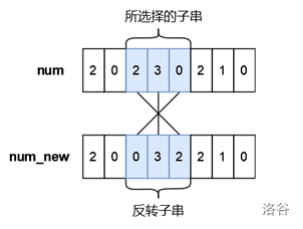
小蓝有一个长度均为 n n n 且仅由数字字符 0 ∼ 9 0 \sim 9 0∼9 组成的字符串,下标从 0 0 0 到 n − 1 n-1 n−1,你可以将其视作是一个具有 n n n 位的十进制数字 n u m num num,小蓝可以从 n u m num num 中选出一段连续的子串并将子串进行反转,最多反转一次。小蓝想要将选出的子串进行反转后再放入原位置处得到的新的数字 n u m n e w num_{new} numnew 满足条件 n u m n e w < n u m num_{new}<num numnew<num,请你帮他计算下一共有多少种不同的子串选择方案,只要两个子串在 n u m num num 中的位置不完全相同我们就视作是不同的方案。
注意,我们允许前导零的存在,即数字的最高位可以是 0 0 0,这是合法的。
输入格式
输入一行包含一个长度为 n n n 的字符串表示 n u m num num(仅包含数字字符 0 ∼ 9 0 \sim 9 0∼9),从左至右下标依次为 0 ∼ n − 1 0 \sim n-1 0∼n−1。
输出格式
输出一行包含一个整数表示答案。
样例 #1
样例输入 #1
210102
样例输出 #1
8
提示
【样例说明】
一共有 8 8 8 种不同的方案:
- 所选择的子串下标为 0 ∼ 1 0\sim1 0∼1,反转后的 n u m n e w = 120102 < 210102 num_{new} = 120102 < 210102 numnew=120102<210102;
- 所选择的子串下标为 0 ∼ 2 0\sim2 0∼2,反转后的 n u m n e w = 012102 < 210102 num_{new} = 012102 < 210102 numnew=012102<210102;
- 所选择的子串下标为 0 ∼ 3 0\sim3 0∼3,反转后的 n u m n e w = 101202 < 210102 num_{new} = 101202 < 210102 numnew=101202<210102;
- 所选择的子串下标为 0 ∼ 4 0\sim4 0∼4,反转后的 n u m n e w = 010122 < 210102 num_{new} = 010122 < 210102 numnew=010122<210102;
- 所选择的子串下标为 0 ∼ 5 0\sim5 0∼5,反转后的 n u m n e w = 201012 < 210102 num_{new} = 201012 < 210102 numnew=201012<210102;
- 所选择的子串下标为 1 ∼ 2 1\sim2 1∼2,反转后的 n u m n e w = 201102 < 210102 num_{new} = 201102 < 210102 numnew=201102<210102;
- 所选择的子串下标为 1 ∼ 4 1\sim4 1∼4,反转后的 n u m n e w = 201012 < 210102 num_{new} = 201012 < 210102 numnew=201012<210102;
- 所选择的子串下标为 3 ∼ 4 3\sim4 3∼4,反转后的 n u m n e w = 210012 < 210102 num_{new} = 210012 < 210102 numnew=210012<210102。
【评测用例规模与约定】
对于 20 % 20\% 20% 的评测用例, 1 ≤ n ≤ 100 1 \le n \le 100 1≤n≤100;
对于 40 % 40\% 40% 的评测用例, 1 ≤ n ≤ 1000 1 \le n \le 1000 1≤n≤1000;
对于所有评测用例, 1 ≤ n ≤ 5000 1 \le n \le 5000 1≤n≤5000。
思路
首先从输入中读取字符串,并获取字符串长度。然后初始化一个二维数组dp,用于存储从索引i到索引j的子串选择方案数。
对于长度为2的子串,如果第一个字符大于第二个字符,那么反转后的数字会小于原数字,所以将dp[i][i+1]设为1,否则设为0。
接下来是一个嵌套循环,外循环遍历所有可能的子串长度,从3开始,因为长度为2的子串已经处理过。内循环遍历所有可能的子串起始位置。
状态转移方程为:
- 如果 s i s_i si 等于 s j s_j sj,那么:
d p [ i ] [ j ] = d p [ i + 1 ] [ j − 1 ] dp[i][j] = dp[i+1][j-1] dp[i][j]=dp[i+1][j−1]
- 如果 s i s_i si 不等于 s j s_j sj,那么:
d p [ i ] [ j ] = { 1 , if s i > s j 0 , otherwise dp[i][j] = \begin{cases} 1, & \text{if } s_i > s_j \\ 0, & \text{otherwise} \end{cases} dp[i][j]={1,0,if si>sjotherwise
d p [ i ] [ j ] dp[i][j] dp[i][j] 表示从索引 i i i 到索引 j j j 的子串选择方案数, s i s_i si 和 s j s_j sj 分别是字符串 s s s 的第 i i i 个字符和第 j j j 个字符。 d p [ i + 1 ] [ j − 1 ] dp[i+1][j-1] dp[i+1][j−1] 表示除去首尾字符后的子串选择方案数。
对于每个子串,如果首尾字符相等,那么子串反转后的数字是否小于原数字取决于除去首尾字符后的子串,即dp[i+1][j-1]。如果首尾字符不相等,那么只有当首字符大于尾字符时,子串反转后的数字才会小于原数字,所以将dp[i][j]设为1,否则设为0。
最后遍历dp数组,将所有dp[i][j]加起来,得到的就是所有可能的子串选择方案数。
AC代码
#include <algorithm>
#include <cstring>
#include <iostream>
#define AUTHOR "HEX9CF"
using namespace std;
using ll = long long;
const int N = 5e3 + 7;
const int INF = 0x3f3f3f3f;
const ll MOD = 1e9 + 7;
int n;
string s;
// 从i到j的方案数
ll dp[N][N];
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
cin >> s;
int len = s.length();
memset(dp, 0, sizeof(dp));
for (int i = 0; i < len - 1; i++) {
dp[i][i + 1] = (s[i] > s[i + 1]);
}
// 区间大小从小到大
for (int k = 3; k <= len; k++) {
for (int i = 0; i + k - 1 < len; i++) {
int j = i + k - 1;
// cout << i << " " << j << endl;
if (s[i] == s[j]) {
dp[i][j] = dp[i + 1][j - 1];
} else {
dp[i][j] = (s[i] > s[j]);
}
}
}
ll ans = 0;
for (int i = 0; i < len; i++) {
for (int j = i + 1; j < len; j++) {
ans += dp[i][j];
}
}
cout << ans << endl;
return 0;
}