꒰˃͈꒵˂͈꒱ write in front ꒰˃͈꒵˂͈꒱
ʕ̯•͡˔•̯᷅ʔ大家好，我是xiaoxie.希望你看完之后,有不足之处请多多谅解，让我们一起共同进步૮₍❀ᴗ͈ . ᴗ͈ აxiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
本文由xiaoxieʕ̯•͡˔•̯᷅ʔ 原创 CSDN 如需转载还请通知˶⍤⃝˶
个人主页：xiaoxieʕ̯•͡˔•̯᷅ʔ—CSDN博客
系列专栏：xiaoxie的JAVA系列专栏——CSDN博客●'ᴗ'σσணღ*
我的目标:"团团等我💪( ◡̀_◡́ ҂)" 

( ⸝⸝⸝›ᴥ‹⸝⸝⸝ )欢迎各位→点赞👍 + 收藏⭐️ + 留言📝​+关注（互三必回）!

​

一.红黑树的概念

红黑树，是一种二叉搜索树，但在每个结点上增加一个存储位表示结点的颜色，可以是Red或Black。 通过对任何 一条从根到叶子的路径上各个结点着色方式的限制，红黑树确保没有一条路径会比其他路径长出两倍，因而是接近平衡的。

二.红黑树的性质

1. 每个结点不是红色就是黑色

2. 根节点是黑色的

3. 如果一个节点是红色的，则它的两个孩子结点是黑色的【没有2个连续的红色节点】

4. 对于每个结点，从该结点到其所有后代叶结点的简单路径上，均 包含相同数目的黑色结点

5. 每个叶子结点都是黑色的(此处的叶子结点指的是空结点) 

三.红黑树的插入

红黑树是在二叉搜索树的基础上加上其平衡限制条件，因此红黑树的插入可分为两步：

1. 按照二叉搜索的树规则插入新节点

2. 检测新节点插入后，红黑树的性质是否造到破坏 因为新节点的默认颜色是红色，因此：如果其双亲节点的颜色是黑色，没有违反红黑树任何性质，则不需要 调整；但当新插入节点的双亲节点颜色为红色时，就违反了性质三不能有连在一起的红色节点，此时需要对 红黑树分情况来讨论： 

 这里解释一下为什么新插入的节点是红色的,因为假如插入节点的节点是黑色的,那么为了要满足性质4对于每个结点，从该结点到其所有后代叶结点的简单路径上，均包含相同数目的黑色结点就需要再插入节点为了满足性质4,这样就浪费很多空间,而要是新插入的节点是红色的,我们只需要调整颜色即可.

约定:cur为当前节点，p为父节点，g为祖父节点，u为叔叔节点

1.情况一: cur为红，p为红，g为黑，u存在且为红

出现这种情况情况,我们先需要把p和u 变成黑色,然后再把g变成红色即可.

这个时候,还需要考虑到

1.g为根节点,只需要在调整结束后,把它变为黑色即可

2.g有双亲节点,且为红色就需要将g当成cur,继续向上调整。(如果双亲节点,为黑色,p和g 变成黑色,然后再把g变成红色后就不违反红黑树的性质了)

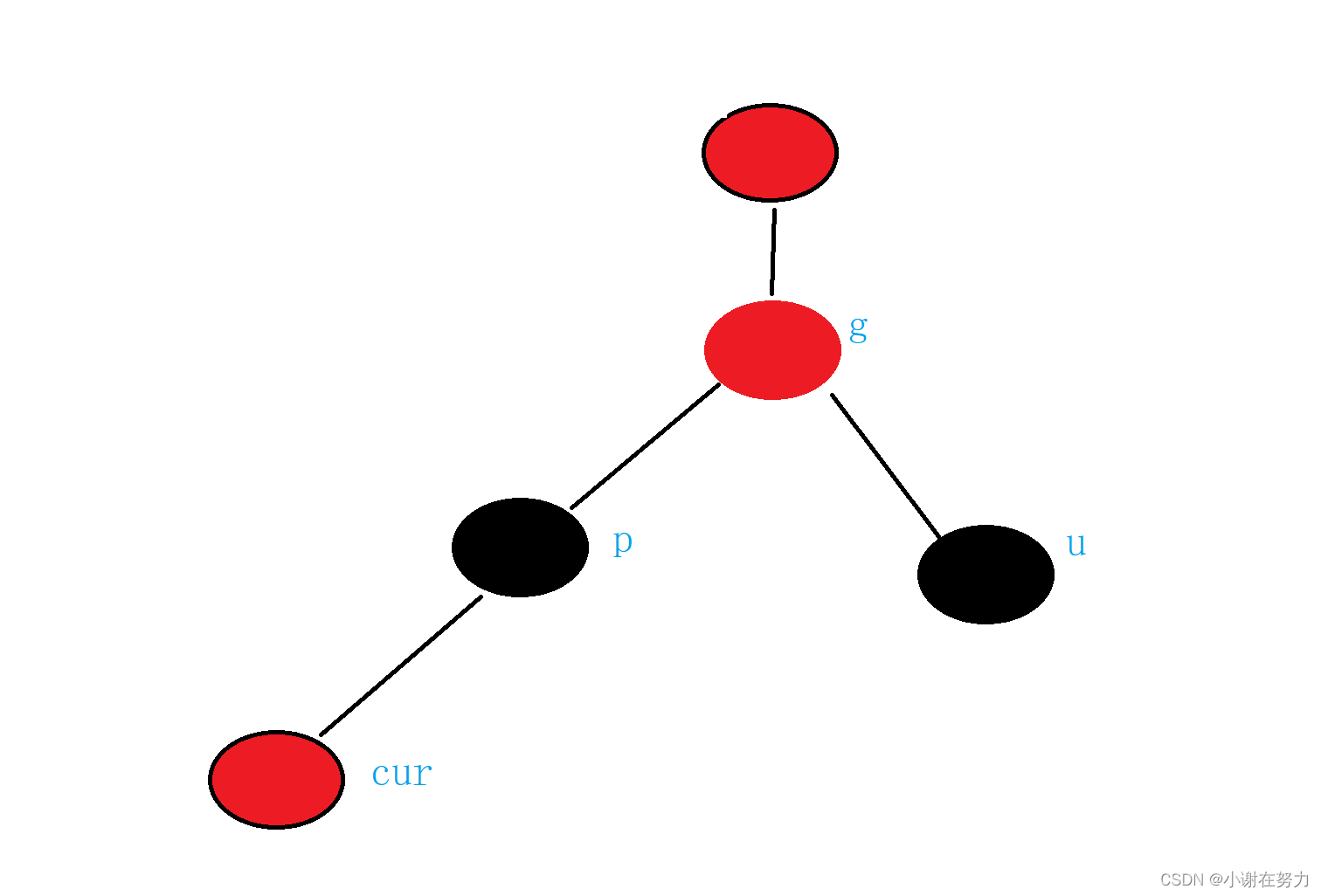
这里再解释一下为什么要把把p和u变成黑色,然后再把g变成红色.

1.首先把p变成红色是因为cur为红色,p也为红色的话就违反了性质3,不能有两个连续的红色节点,所以需要把p变成黑色.

2.为什么要把u变成黑色是因为性质4,每条路径要有相同路径的黑色节点,如果u为红色,p为黑色就不满足该性质,所以要把u变成黑色

3.为什么要把g变成红色,因为假如g还有双亲节点的话,且双亲节点为黑色,那么,由于p和u变成了黑色,为了要满足,性质4,每条路径要有相同路径的黑色节点,就需要增加黑色节点的个数,所以需要把g变成红色,p和u变成黑色,就满足了性质4

 2.情况二:cur为红，p为红, g为黑，u不存在/u为黑

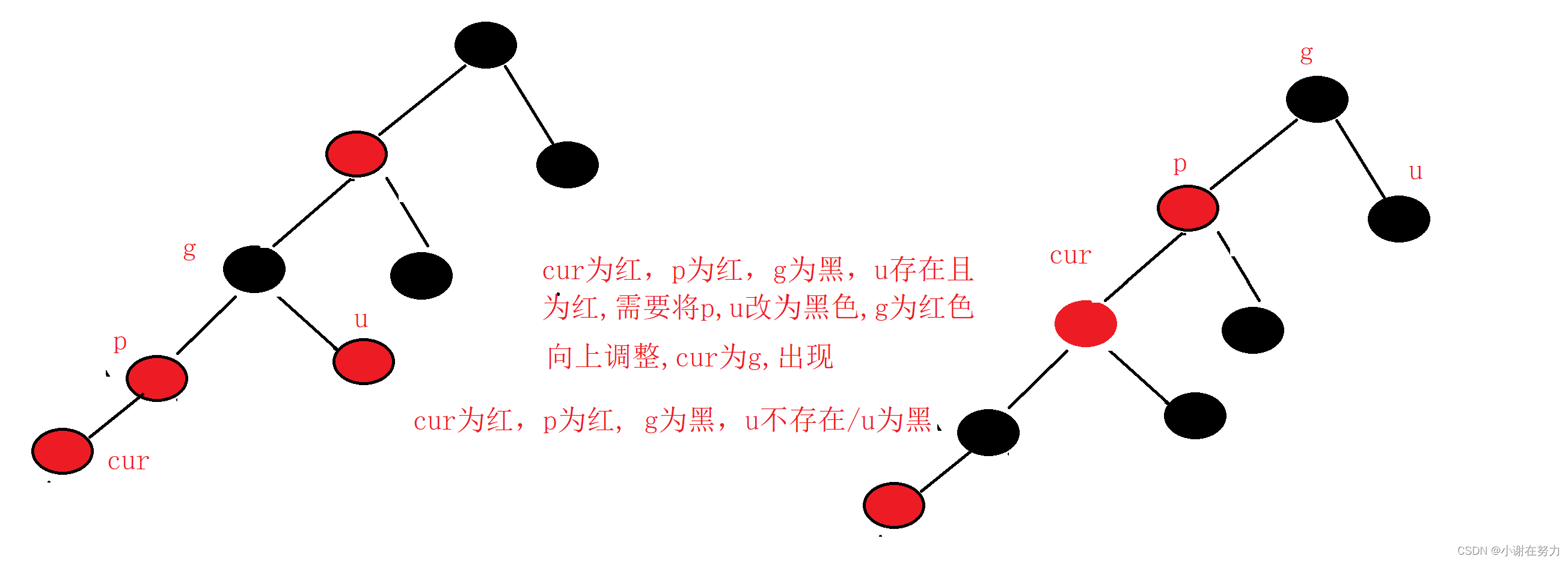
就是因为在出现情况一之后,调整,p,u,g的颜色导致了情况二的发生

我们该如何调整调整使它满足红黑树的五条性质呢,我们可以发现,仅仅简单的改变颜色并不可以满足红黑树的五条性质,这个时候我们可以发现,这个情况是不是很像AVL树树中的左树高于,右数的情况,这个时候对于AVL树来说,可以使用右旋来解决这个问题,我们是不是也可以通过旋转操作可以调整节点的位置,然后只要在稍微改变个边节点的颜色即使它满足红黑树的性质.

右旋后再根据红黑树的性质,把g变为红色,p变为黑色,即可 

3.情况三: cur为红，p为红，g为黑，u不存在/u为黑 

在调整的过程中,cur变成了红色,导致情况三的发生, 同时,我们发现和AVL树类似,仅仅通过左旋或者右旋并不可以可以调整节点的位置,因为是较高左树的右子树较高,我们先进行,左旋.

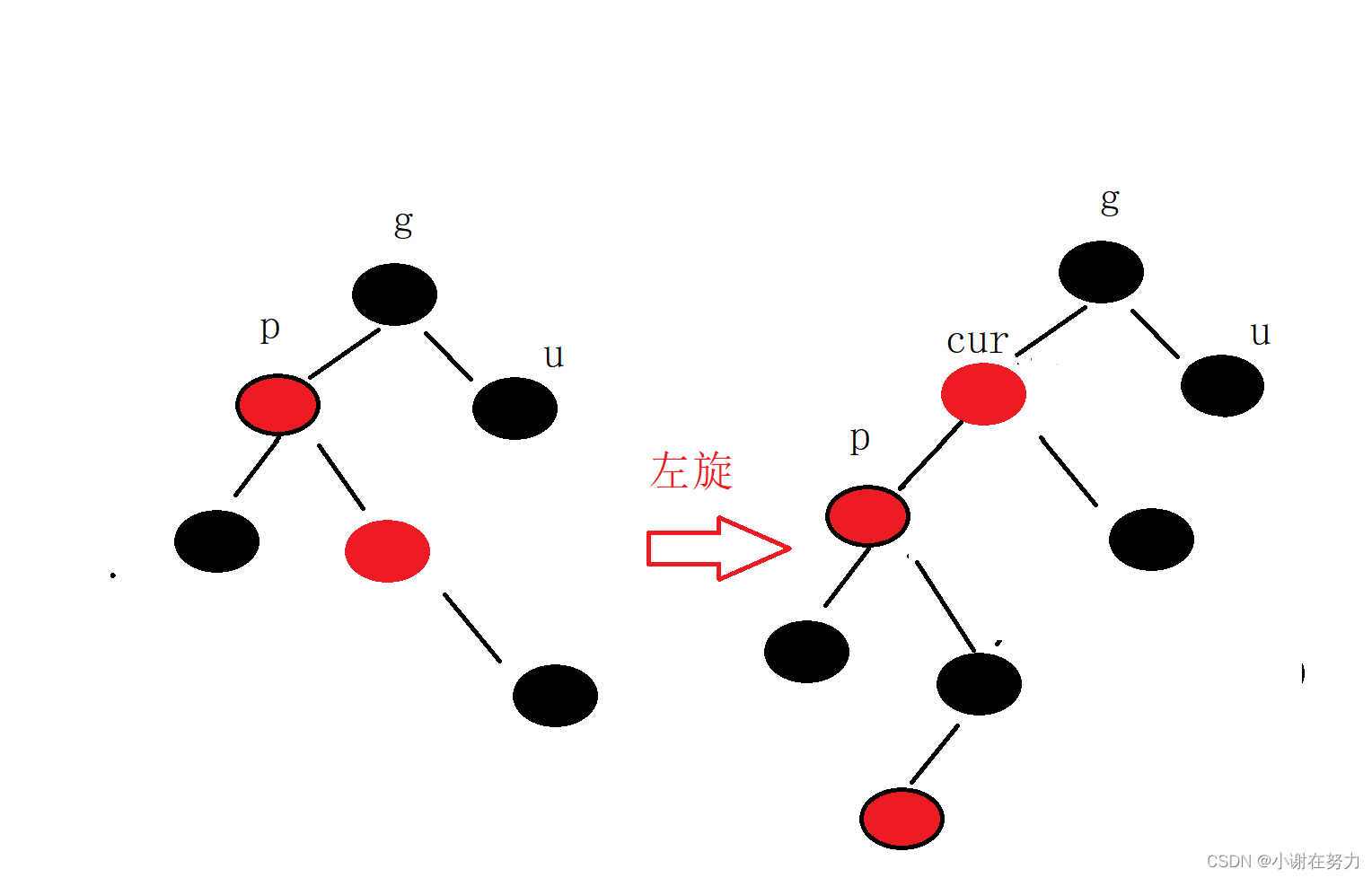
通过左旋我们发现,可以把问题转换为情况二,即可解决该问题.

4.说明

从上面的这些情况我们可以发现,在上面这些图中,p都为g的左孩子的情况,p为g右孩子的情况我并没有说明,在这里博主统一说明一下,因为p为g右孩子的情况就是p都为g的左孩子的情况的相当于镜像处理即

在情况二中

p为g的左孩子，cur为p的左孩子，则进行右单旋转；相反， p为g的右孩子，cur为p的右孩子，则进行左单旋转

在情况三中

p为g的左孩子，cur为p的右孩子，则针对p做左单旋转；相反， p为g的右孩子，cur为p的左孩子，则针对p做右单旋转

所以博主就不展示调整过程了,直接上代码

5.代码实现

public class RBTree {
    public static enum COLOR {RED, BLACK} // 定义颜色枚举，表示节点的红黑状态

    // 红黑树节点类
    public static class RbTreeNode {
        public RbTreeNode left;  // 左子节点
        public RbTreeNode right; // 右子节点
        public RbTreeNode parent; // 父节点
        public int val;          // 节点值
        public COLOR color;      // 节点颜色，默认为红色

        // 构造函数，创建一个带有指定值的新节点，并将其颜色设置为红色
        public RbTreeNode(int val) {
            this.val = val;
            this.color = COLOR.RED;
        }
    }

    // 树的根节点
    public RbTreeNode root;

    // 插入新节点方法
    public boolean insert(int val) {
        RbTreeNode node = new RbTreeNode(val);
        if(root == null) {
            root = node;
            return true;
        }

        // 寻找插入位置
        RbTreeNode cur = root;
        RbTreeNode parent = null;
        while (cur != null) {
            if(node.val < cur.val) {
                parent = cur;
                cur = cur.left;
            } else if(node.val > cur.val) {
                parent = cur;
                cur = cur.right;
            } else {
                System.out.println("这个节点" + val +"已经存在了");
                return false;
            }
        }

        // 插入新节点并更新父节点指向
        if(parent.val < node.val) {
            parent.right = node;
        } else {
            parent.left = node;
        }
        node.parent = parent;

        // 调整红黑树性质
        cur = node;
        while (parent != null && parent.color == COLOR.RED) {
            RbTreeNode grandfather = parent.parent;
                if(parent == grandfather.left) {//p节点为g节点的左孩子
                RbTreeNode uncle = grandfather.right;
                //uncle不为空,且uncle的颜色为红色
            // 获取叔叔节点
          
            // 情况一：叔叔节点存在且为红色
            if(uncle != null && uncle.color == COLOR.RED) {
                grandfather.color = COLOR.RED;
                parent.color = COLOR.BLACK;
                uncle.color = COLOR.BLACK;
                cur = grandfather;
                parent = cur.parent;
            } else {
                // 情况三：叔叔节点不存在或为黑色
                if(cur == parent.right) { // 需要左旋
                    rotateLeft(parent);
                    RbTreeNode tmp = parent;
                    parent = cur;
                    cur = tmp;
                }
                //情况二:叔叔节点不存在或为黑色
                rotateRight(grandfather); // 右旋以修复红黑树性质
                grandfather.color = COLOR.RED;
                parent.color = COLOR.BLACK;
            }else {///p节点为g节点的右孩子//镜像处理和/p节点为g节点的左孩子类似
                 RbTreeNode uncle = grandfather.left;
                if(uncle != null && uncle.color == COLOR.RED) {
                    grandfather.color = COLOR.RED;
                    parent.color = COLOR.BLACK;
                    uncle.color = COLOR.BLACK;
                    cur = grandfather;
                    parent = cur.parent;
                }else {
                    //情况三
                    if(cur == parent.left) {
                        rotateRight(parent);
                        RbTreeNode tmp = parent;
                        parent = cur;
                        cur = tmp;
                    }
                    //情况二
                    //叔叔节点不存在 || 叔叔节点存在，但是颜色是黑色
                    rotateLeft(grandfather);
                    grandfather.color = COLOR.RED;
                    parent.color = COLOR.BLACK;
                }
        }

        return true;
    }

    /**
     * 右旋操作
     * @param parent 需要右旋的节点（旋转中心）
     */
    private void rotateRight(RbTreeNode parent) {
        RbTreeNode subL = parent.left;
        RbTreeNode subLR = subL.right;

        subL.right = parent;
        parent.left = subLR;

        if(subLR != null) {
            subLR.parent = parent;
        }

        RbTreeNode Pparent = parent.parent;
        parent.parent = subL;

        if(parent == root) {
            root = subL;
            root.parent = null;
            root.color = COLOR.BLACK;//如果是根节点就要为黑色
        } else {
            if(Pparent.left == parent) {
                Pparent.left = subL;
            } else {
                Pparent.right = subL;
            }
            subL.parent = Pparent;
        }
    }

    /**
     * 左旋操作
     * @param parent 需要左旋的节点（旋转中心）
     */
    private void rotateLeft(RbTreeNode parent) {
        RbTreeNode subR = parent.right;
        RbTreeNode subRL = subR.left;

        subR.left = parent;
        parent.right = subRL;

        if(subRL != null) {
            subRL.parent = parent;
        }

        // 记录parent节点的父亲节点
        RbTreeNode Pparent = parent.parent;
        parent.parent = subR;

        if(parent == root) {
            root = subR;
            subR.parent = null;
            root.color = COLOR.BLACK;//如果是根节点就要为黑色
        } else {
            if(Pparent.left == parent) {
                Pparent.left = subR;
            } else {
                Pparent.right = subR;
            }
            subR.parent = Pparent;
        }
    }
}

好了，这三种情况都讨论完了，我想强调的是：注意哪些分方向的情况，每个分方向的情形就两种情况

四.红黑树验证

这里博主在提供一下红黑树验证的方法,检测一下你自己手撕红黑树代码有没有错误

1. 检测其是否满足二叉搜索树(中序遍历是否为有序序列)

public void inorder(RBTreeNode root) {
if(root == null) {
return;
}
inorder(root.left);
System.out.print(root.val+" ");
inorder(root.right);
}

2.检测其是否满足红黑树的性质

public boolean isValidRBTree()
{
// 空树也是红黑树
if(null == root)
return true;
if(root.color != COLOR.BLACK) {
System.out.println("违反了性质2：根节点不是黑色");
return false;
}
// 获取单条路径中节点的个数
int blackCount = 0;
RBTreeNode cur = root;
while(null != cur){
if(cur.color == COLOR.BLACK)
blackCount++;
cur = cur.left;
}
// 具体的检验方式
return _isValidRBtree(root, 0, blackCount);
}
private boolean _isValidRBtree(RBTreeNode root, int pathCount, int blackCount){
if(null == root)
return true;
// 遇到一个黑色节点，统计当前路径中黑色节点个数
if(root.color == COLOR.BLACK)
pathCount++;
// 验证性质4
RBTreeNode parent = root.parent;
if(parent != null && parent.color == COLOR.RED && root.color == COLOR.RED){
System.out.println("违反了性质4：有连在一起的红色节点");
return true;
}
// 验证性质5
// 如果是叶子节点，则一条路径已经走到底，检验该条路径中黑色节点总个数是否与先前统计的结果相同
if(root.left == null && root.right == null){
if(pathCount != blackCount){
System.out.println("违反了性质5：路径中黑色节点格式不一致");
return false;
}
}
// 以递归的方式检测root的左右子树
return _isValidRBtree(root.left, pathCount, blackCount) &&
_isValidRBtree(root.right, pathCount, blackCount);
}

5. AVL树和红黑树的比较

红黑树和AVL树都是高效的平衡二叉树，增删改查的时间复杂度都是O(logN )，红黑树不追求绝对平衡，其只需保 证最长路径不超过最短路径的2倍，相对而言，降低了插入和旋转的次数，所以在经常进行增删的结构中性能比 AVL树更优，而且红黑树实现比较简单，所以实际运用中红黑树更多。