一,MATLAB的编程特点
a,语法高度简化;
b,脚本式解释型语言;
c,针对矩阵的高性能运算;
d,丰富的函数工具箱支持;
e,通过matlab本体构建跨平台;
二,MATLAB的界面

工具栏:提供快捷操作编辑器:
脚本代码窗口工作区:
脚本变量窗口工作路径:
当前文件运行的检索路径
三,MATLAB的工具栏
新建脚本:新建脚本或函数(*.m)文件
新建实时脚本:新建可交互脚本(*.mlx)文件
新建/打卡:支持更加泛化的新建/打开文件类型导入数据:加载可识别的数据文件
保存工作区:将工作区的文件保存至(*.mat)文件
Simulink:打开可视化仿真工具
预设:MATLAB相关参数设置
帮助:查询相关文档和示例
四,常用控制代码
4.1 clc:清空命令行


4.2 clear:清空工作区变量


4.3 clear all:清空工作区(在一般matlab使用中等价于clear)
4.4 close:关闭当前图像窗口
4.5 *dbstop if error:建立变量缓冲区,在错误位置自动断点调试
编译器会报错,在错误的地方停止运行

4.6 Crtl + R/crtl + T:注释和反注释(支持批量)
4.7 ctrl + C: 强制停止
4.8 crtl + R:智能缩进
4.9 F9:在命令行中运行编译器内代码
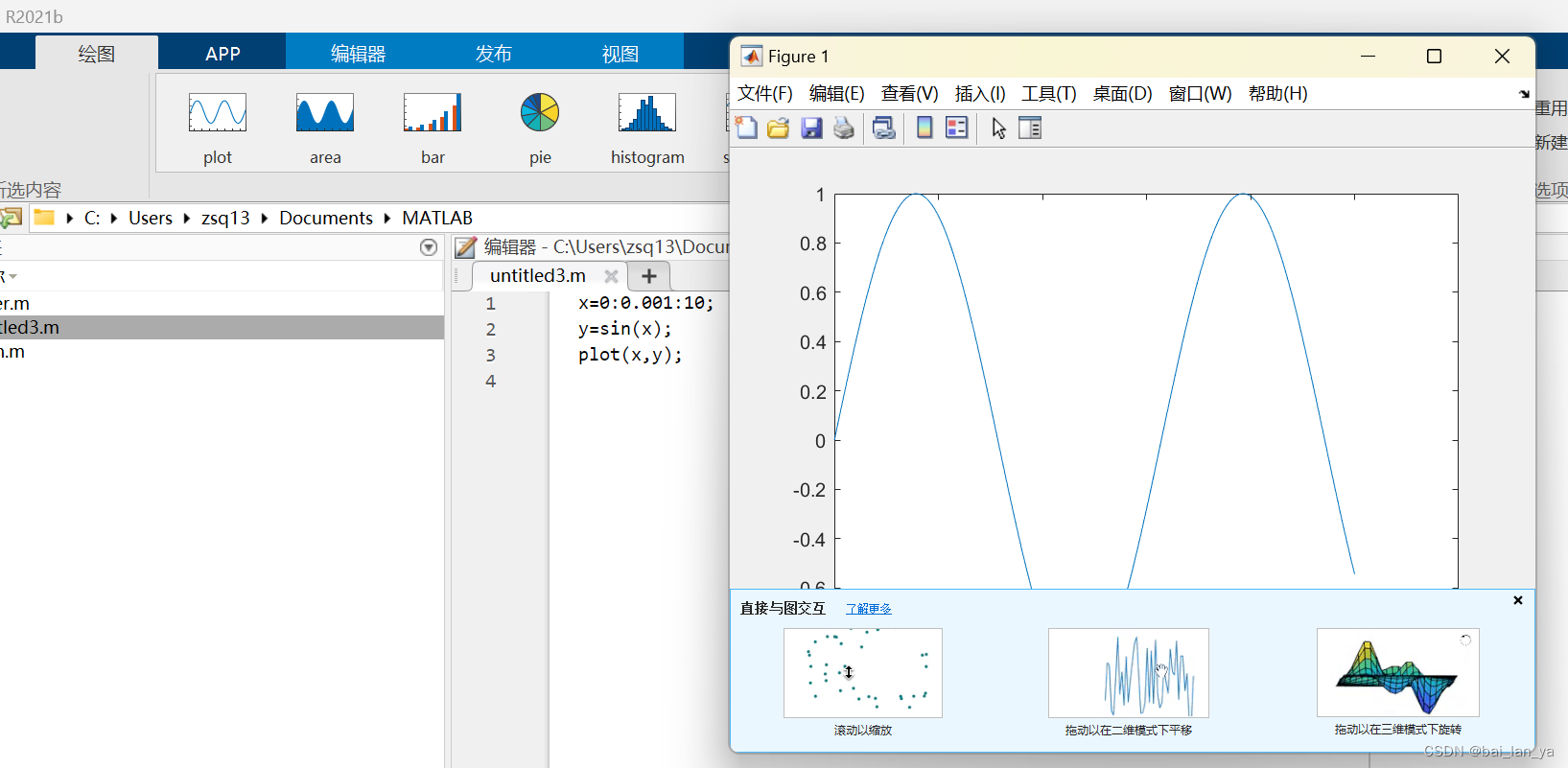
五,MATLAB运算
命令行==计算器?
1,加+ 减- 乘* 除 /

2,平方根 sqrt(),任意次幂()^();power(,)

4,对数 log();log10();log2(); log1p()

5,指数exp();expm1();pow2();nextpow2()

6,三角函数 sin( );cos(); sinpi( );cospi();tan( )

7,反三角函数 asin( );acos( );asind();acosd( );atan( );atand( ); atan2()

六,MATLAB整体运算
1 模与余数 mod(,)rem(,)

2,符号函数sign()

3,matlab小数计算

4,matlab整体运算

5,生成随机数
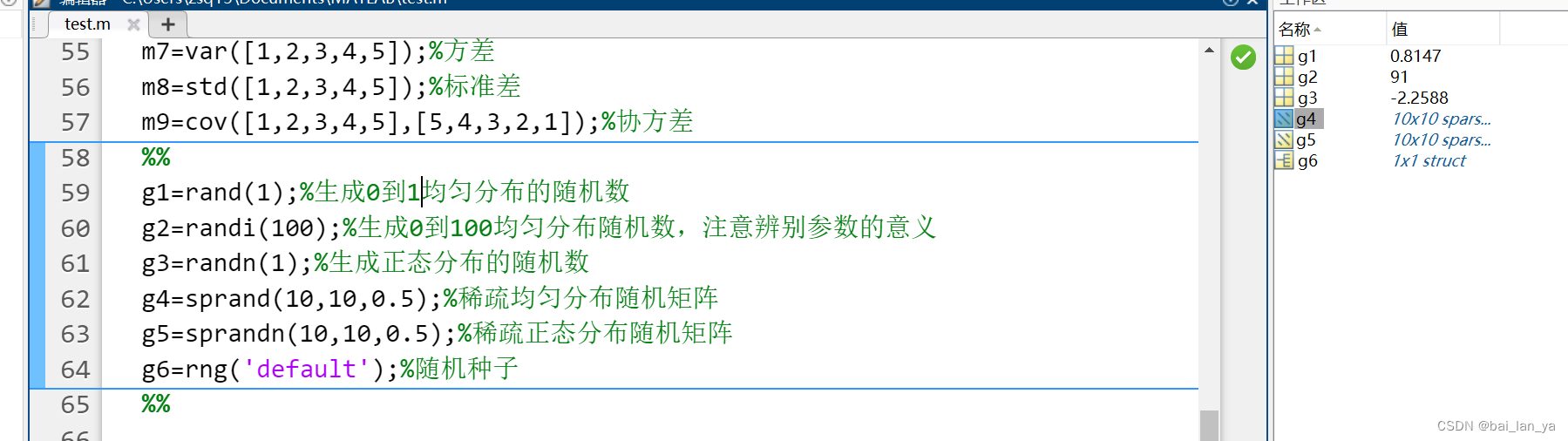
七,矩阵
1,矩阵的重要性
矩阵是MATLAB的核心
MATLAB通过建立特定平台进行大量的硬件针对性优化
2,创建向量
特殊的矩阵形式:向量。
生成格式:
①起始数据:数据间隔(可忽略,默认为1):结束数据
示例:
1:100(等价于1:1:100) 范围为1到100,间隔为1,1*100的向量
1:2:100 范围为1到100,间隔为2,1*50的向量
100:-1:1 范围为1到100,间隔为-1,1*100的向量
1:1:100.7 范围为1到100(<=100.7的最大整数),间隔为1,1*100的向量
②特殊异常模式(三冒号表达式)A:B:C:D
>>1:2:4:5 >>2:-1:3:5
ans = ans =
1 2 3 4 5 空的 1*0 的double行向量
无用形式,但不会报错
3,赋值方法
[3.4] 创建了值为3.4的1乘1矩阵(标量)
[1.0,2.0,3.0] 创建了值为[1 2 3]的1乘3矩阵(行向量)
[1.0 2.0 3.0] 创建了值为[1 2 3]的1乘3矩阵(行向量)
[1.0; 2.0; 3.0] 创建了值为[1 2 3]^T的3乘1矩阵(列向量)
[1,2, 3; 4, 5, 6] 创建了值为2*3的矩阵
[1,2,3
4, 5,6] 创建了值为2*3的矩阵
采用逗号或空格来分割行元素
采用分号或换行来分割列元素
4,矩阵快速创建方法


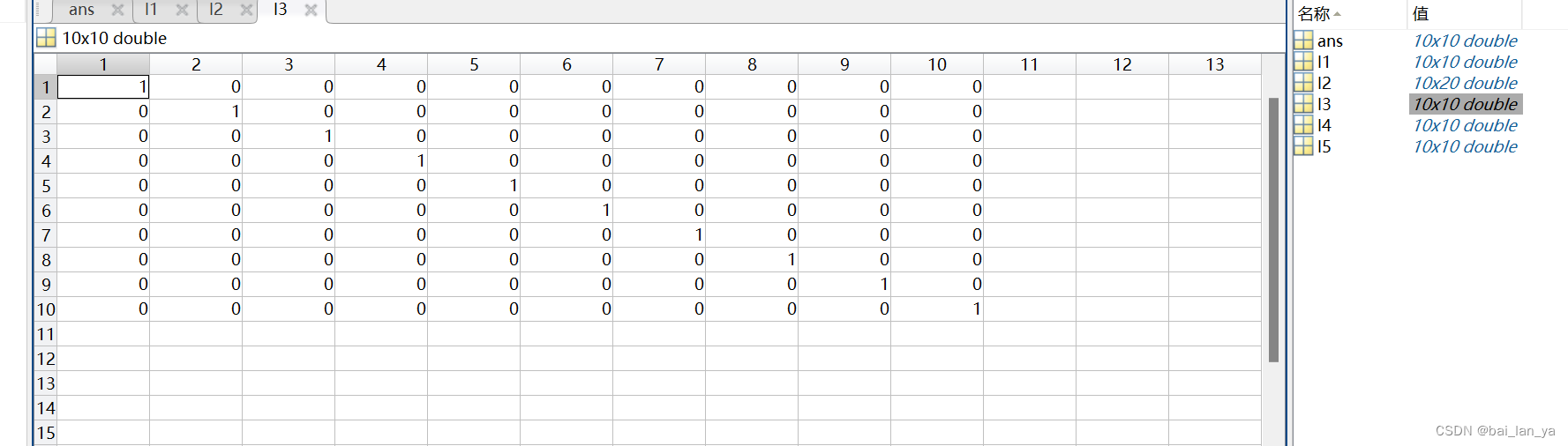
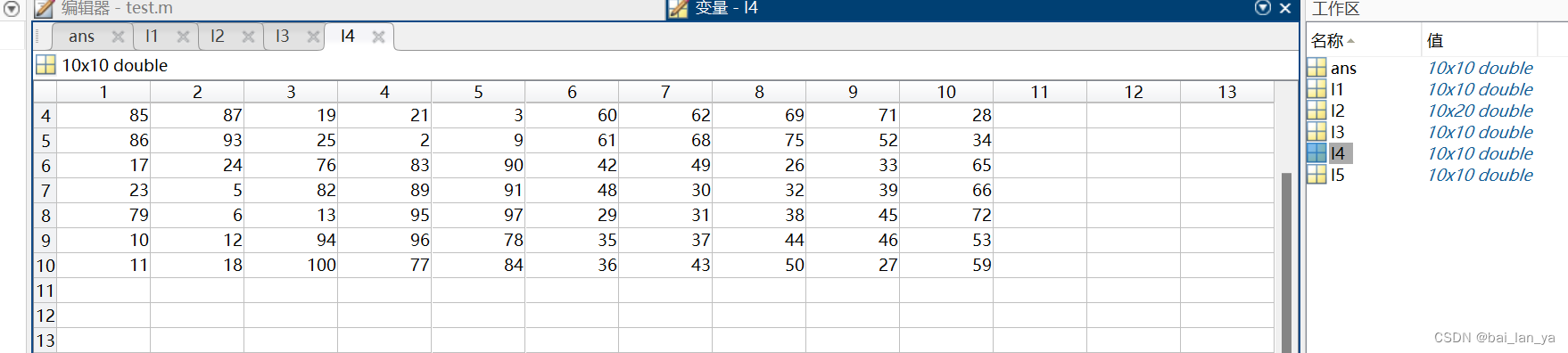


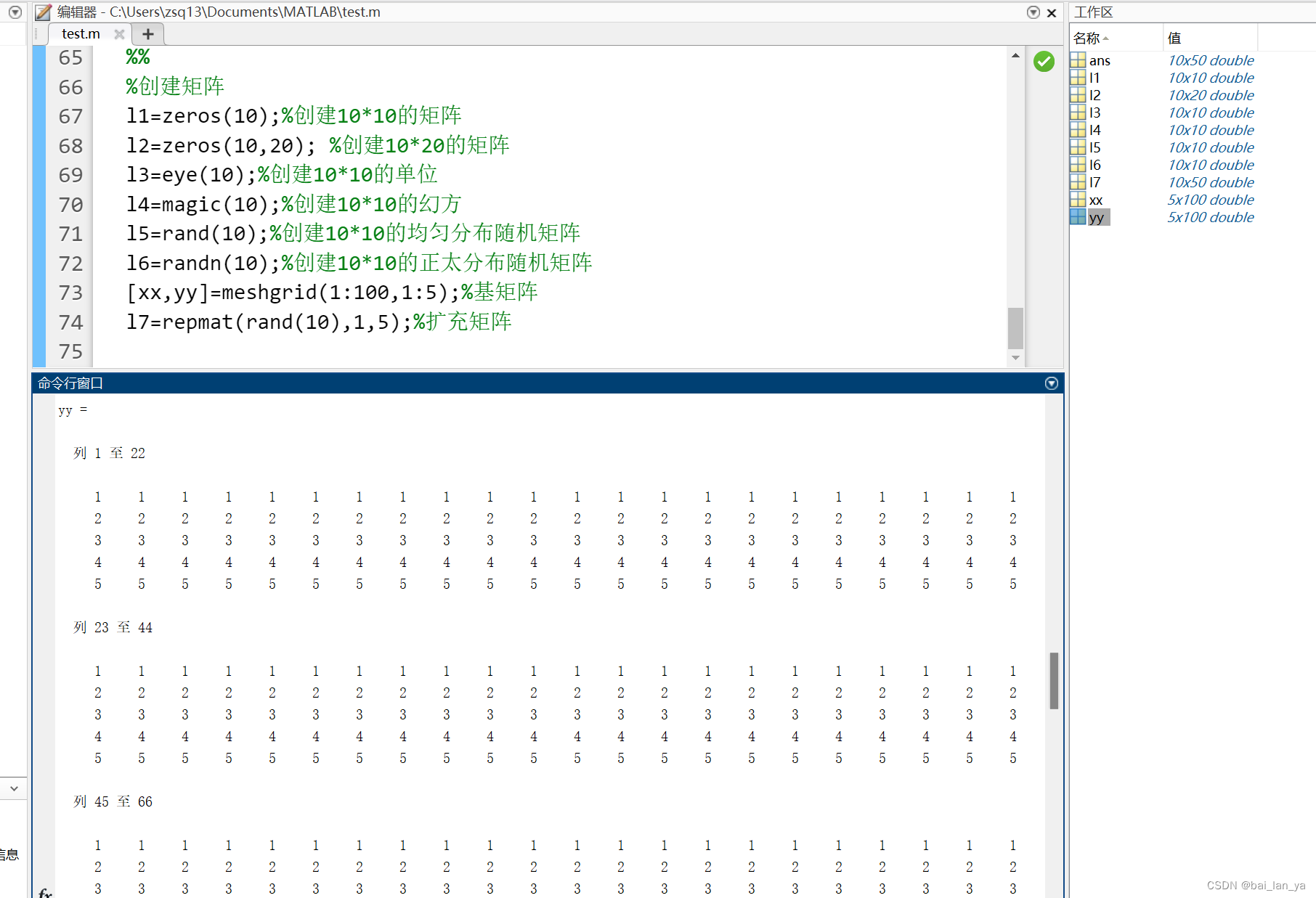
5,矩阵运算模式
矩阵相乘 A*B
矩阵右乘 A/B等价于A*B的逆 注意左除和右除的区别
矩阵左乘 A/B等价于A的逆乘B
矩阵数乘 A.*B
矩阵右除 A./B等价于A除以B 每个元素进行分别操作
矩阵左除 A./B等价于A除B
对于数+/-矩阵,其相当于在矩阵每个元素加减此数



 6,其他运算方法
6,其他运算方法
矩阵A求逆 inv(A)
矩阵A求伪逆 pinv(A) 适用于非方阵和奇异阵
矩阵A求转置 A'
求行列式A det(A)
求行列式A的迹 trace(A)
求矩阵A的LU分解 lu(A)
求矩阵A的QR分解 qr(A)
求矩阵A的特征值与向量 eig(A) 矩阵分析常用

大家可以自己打代码试一下
7,矩阵数据的提取
确定矩阵的大小
length()-用于向量 size()-用于矩阵
元素提取:
A(m,n)表示提取矩阵的第m,n位置处的值
注意m,n不能超出矩阵维度,matlab中起始值为1
冒号/end提取法:
A( :1) 提取矩阵第一列
A(1,: ) 提取矩阵第一行
A(1,end) 提取矩阵第一行中最后一个值
A(2:2:end,:) 提取偶数行
8,矩阵操作
-更改矩阵的大小:
Matrix_out = reshape( Matrix_in , m , n)
m/n为新矩阵的行数和列数
注意在矩阵改变的同时不能改变元素个数
-复制扩充:
Matrix out = repmat( Matrix_in , m , n)
m/n为扩充的行倍数和列倍数
9,交叉知识-稀疏矩阵
采用[(m,n),value]三元组来存储数据,不存储0值以节省空间
直接生成稀疏矩阵:sparse(m,n)
将矩阵A强制转化为稀疏矩阵:sparse(A)
>>one(1e5)
错误使用 ones
请求的100000*100000(74.5GB)数组超过预设的最大数值大小
>>sparse(1e5,1e5)
ans=
全零稀疏矩阵:100000*100000
节省存储空间,对于严重稀疏矩阵加快运算速度
八,逻辑
1,逻辑变量
Logical类型:true(真值),false(假值)
>>a = true
a =
logical
1
*******************************************
>>b=false
b=
logical
0
*******************************************
>>a = true + 1.1
a =
2.1000
*******************************************
逻辑变量可参与运算,参与运算时其默认值为1/0
>>logical(-0.5)
ans=
logical
1
*****************************************************
>>logical(2)
ans=
logical
2
*******************************************************
逻辑类型的强制中,所有非0值(包括字符串)都会转化为真值
2,逻辑判定

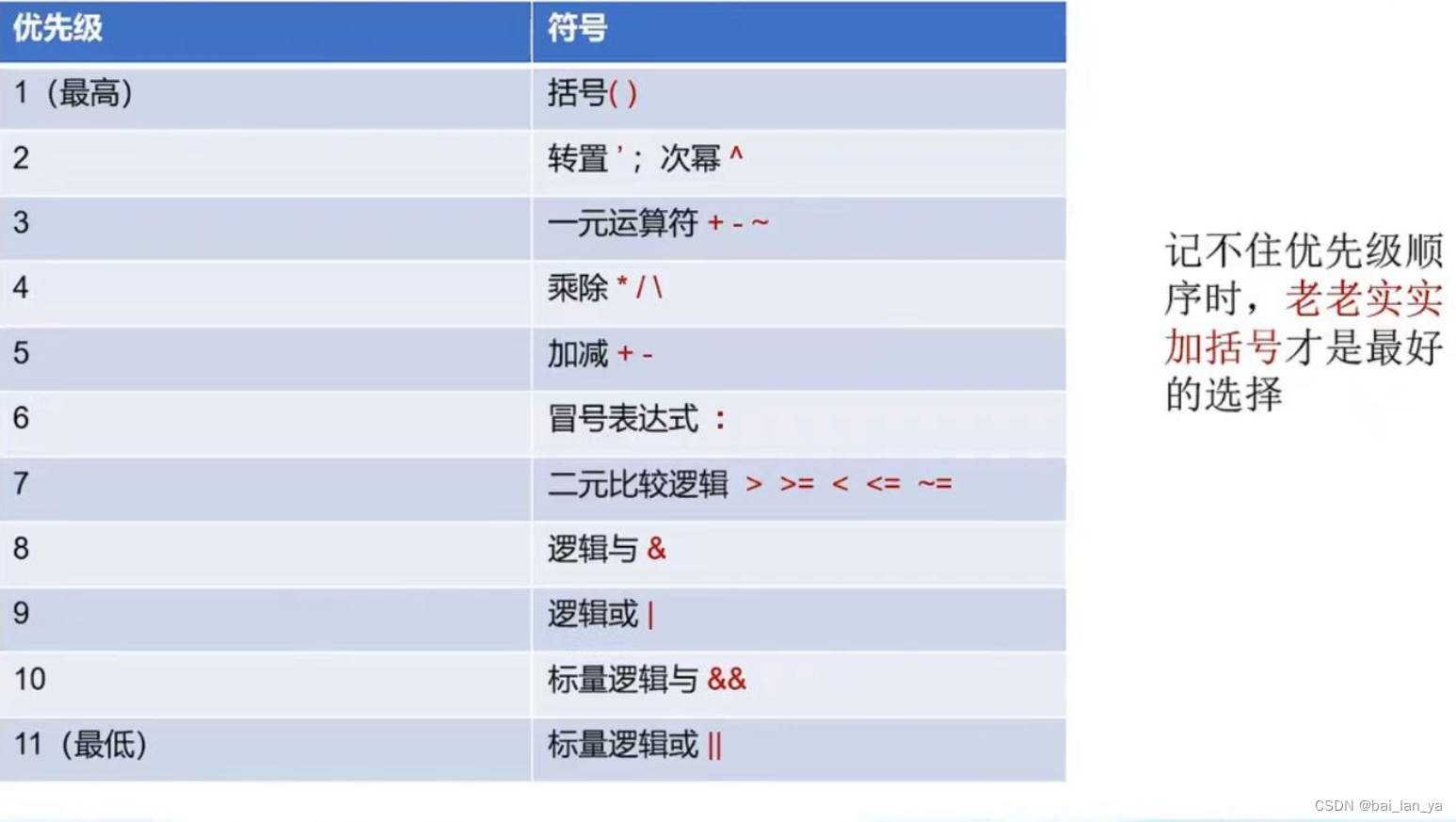
3,逻辑运算

4,优先级